专题03-导数与应用-各类考试必备素材之高三数学(文)全国各地优质金卷-Word版含解析VIP免费

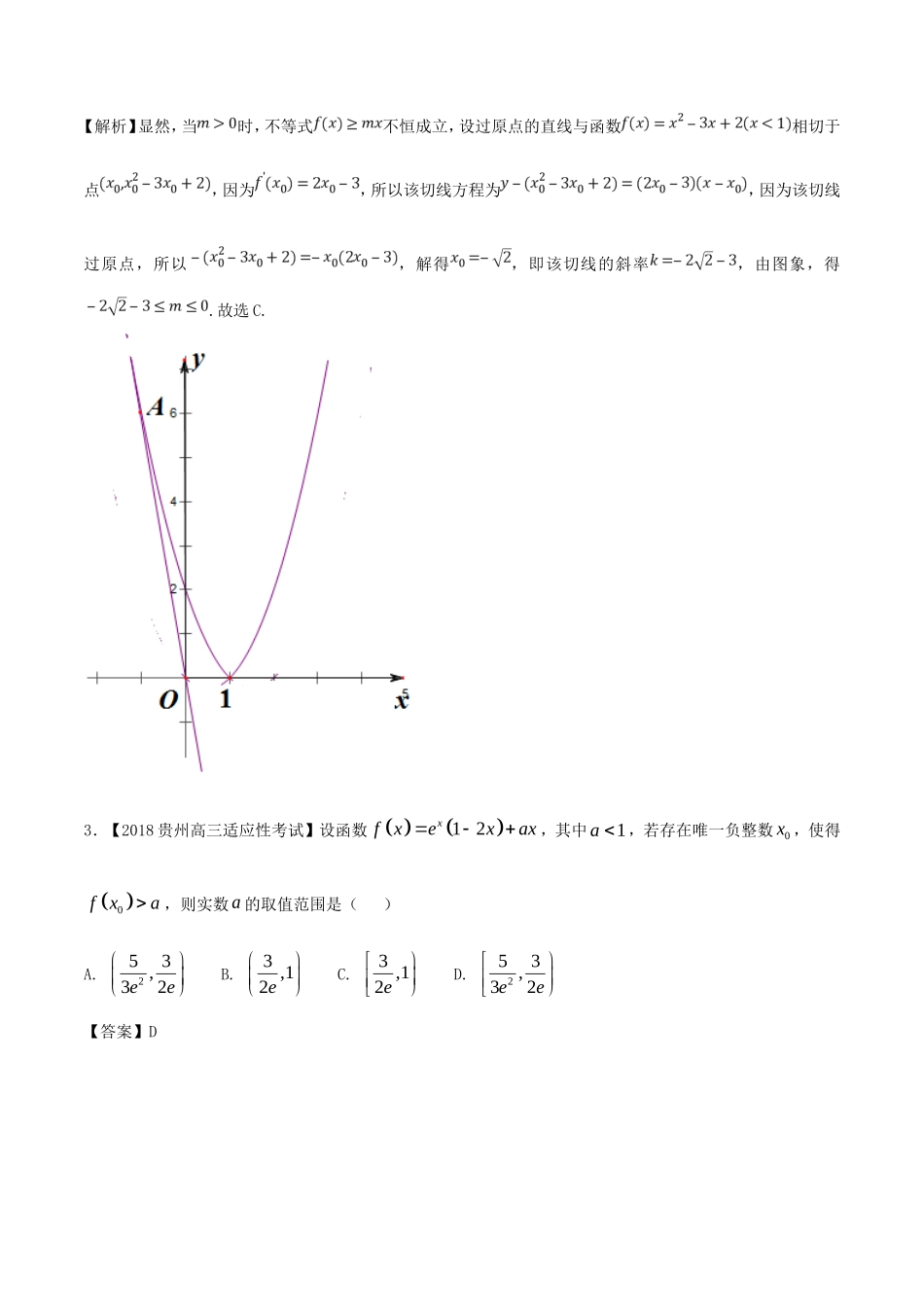
【2018高三数学各地优质二模试题分项精品】专题三导数与应用一、选择题1．【2018全国统一考试高三二调】已知定义在R上的函数恒成立，则不等式的解集为A.B.C.D.【答案】D点睛：本题考查了函数的综合应用问题，以及不等式的求解，着重考查了学生分析问题和解答问题的能力，以及转化与化归思想的应用，对于与函数有关的不等式的求解问题：通常是代入函数的解析式，直接求解不等式的解集，若不等式不易解或不可解，则将问题转化为构造新函数，利用新函数的性质——单调性与奇偶性等，结合函数的图象求解，这样会使得问题变得直观、简单，这也体现了数形结合思想的应用.2．【2018东莞高三二模】已知函数若不等式恒成立，则实数的取值范围为()A.B.C.D.【答案】C【解析】显然，当时，不等式不恒成立，设过原点的直线与函数相切于点，因为，所以该切线方程为，因为该切线过原点，所以，解得，即该切线的斜率，由图象，得.故选C.3．【2018贵州高三适应性考试】设函数12xfxexax，其中1a，若存在唯一负整数0x，使得0fxa，则实数a的取值范围是（）A.253,32eeB.3,12eC.3,12eD.253,32ee【答案】D直线y=ax﹣a恒过定点（1，0）且斜率为a，故﹣a＞g（0）=﹣1且g（﹣1）=﹣3e﹣1﹣a﹣a，g（﹣2）=252aae解得：253e≤a＜32e故选：D．点睛：已知函数有零点求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．4．【2018北京师范大学附中高三二模】设函数，若不等式有正实数解，则实数的最小值为（）A.3B.2C.D.【答案】D5．【2018陕西咸阳高三二模】已知定义在R上的函数fx的导函数为'fx，且'1fxfx，设21af，31bef，则a，b的大小关系为（）A.abB.abC.abD.无法确定【答案】A【解析】令xxgxefxe，则10xxxgxefxfxeefxfx.即gx在R上为增函数.所以32gg，即332232efeefe，整理得：3121eff，即ab.故选A.点睛：本题主要考查构造函数，常用的有：fxxfx，构造xf(x)；2xf(x)+x2f′(x)，构造x2f(x)；xfxfx，构造fxx;fxfx，构造xfxe；fxfx，构造xefx.等等.6．【2018河南商丘高三二模】定义在上的函数满足：，是的导函数，则不等式(其中为自然对数的底数）的解集为（）A.B.C.D.【答案】A点睛：构造函数，再研究函数的性质，再利用函数的性质解题，是函数里的一个常用技巧.本题就利用了这个技巧，先构造函数g(x)=,再分析函数g(x)的单调性和特殊点，最后利用函数的性质解答.7．【2018重庆高三二诊】曲线250xyxy在点1,2A处的切线与两坐标轴所围成的三角形的面积为（）A.9B.496C.92D.113【答案】B【解析】由250xyxy，得52xyfxx，∴232fxx，∴113f，∴曲线在点1,2A处的切线方程为1213yx．令0x，得73y；令0y得7x．∴切线与两坐标轴所围成的三角形的面积为17497236S．选B．8．【2018东北三省四市高三一模】已知过曲线xye上一点00,Pxy作曲线的切线，若切线在y轴上的截距小于0时，则0x的取值范围是（）A.0,B.1,eC.1,D.2,【答案】C9．【2018广东茂名高三二模】若对任意的0x，不等式22ln10xmxm恒成立，则m的取值范围是（）A.1B.1,C.2,D.,e【答案】A【解析】由已知可得22ln10xmx对任意的0x恒成立，设22ln1,fxxmx则2222,xmmfxxxx当0m时0fx在0,上恒成立，fx在0,上单调递增，又10,f在0,1上0,fx不合题意；当0m时...