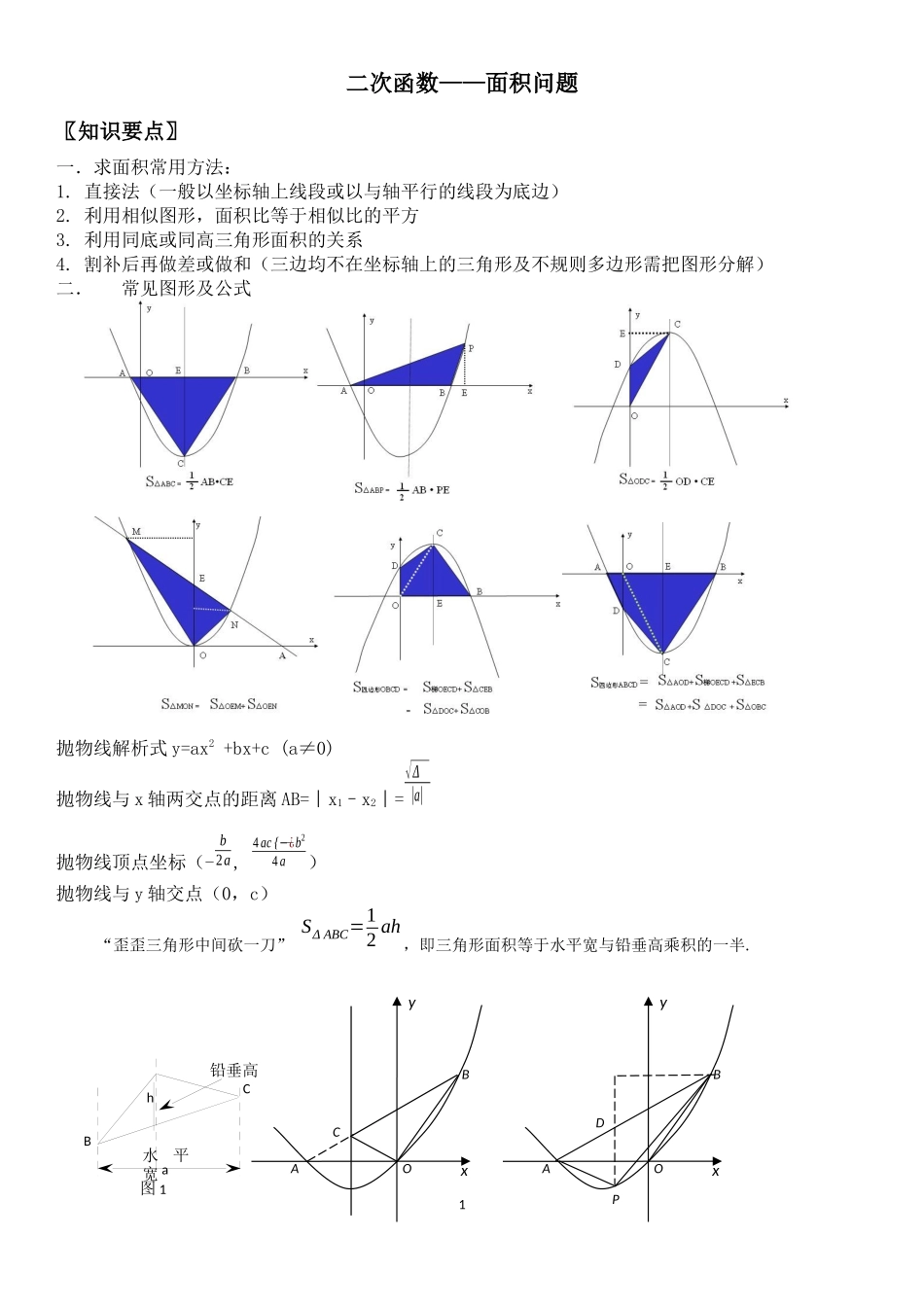
BC铅垂高水平宽ha图1二次函数——面积问题〖知识要点〗一.求面积常用方法:1.直接法(一般以坐标轴上线段或以与轴平行的线段为底边)2.利用相似图形,面积比等于相似比的平方3.利用同底或同高三角形面积的关系4.割补后再做差或做和(三边均不在坐标轴上的三角形及不规则多边形需把图形分解)二.常见图形及公式抛物线解析式y=ax2+bx+c(a≠0)抛物线与x轴两交点的距离AB=︱x1–x2︱=√Δ|a|抛物线顶点坐标(-b2a,4ac{−¿b24a)抛物线与y轴交点(0,c)“歪歪三角形中间砍一刀”SΔABC=12ah,即三角形面积等于水平宽与铅垂高乘积的一半.1xyOABCPxyOABD〖基础习题〗1、若抛物线y=-x2–x+6与x轴交于A、B两点,则AB=,此抛物线与y轴交于点C,则C点的坐标为,△ABC的面积为.2、若抛物线y=x2+4x的顶点是P,与X轴的两个交点是C、D两点,则△PCD的面积是_____________.3、已知抛物线y=x2+bx+c与y轴交于点A,与x轴的正半轴交于B、C两点,且BC=2,S△ABC=3,则b=,c=.〖典型例题〗面积最大问题1、二次函数y=ax2+bx+c的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C,∠ACB=90°.(1)求二次函数的解析式;(2)P为抛物线X轴上方一点,若使得△PAB面积最大,求P坐标(3)P为抛物线X轴上方一点,若使得四边形PABC面积最大,求P坐标(4)P为抛物线上一点,若使得SΔPAB=12SΔABC,求P点坐标。2yxBACO同高情况下,面积比=底边之比2.已知:如图,直线y=x﹣+3与x轴、y轴分别交于B、C,抛物线y=x﹣2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点.(1)求B、C两点的坐标和抛物线的解析式;(2)若点P在直线BC上,且,求点P的坐标.3.已知:m、n是方程x26x﹣+5=0的两个实数根,且m<n,抛物线y=x﹣2+bx+c的图象经过点A(m,0)、B(0,n).(1)求这个抛物线的解析式;(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.3三角形面积等于水平宽与铅垂高乘积的一半4.阅读材料:如图,过△ABC的三个顶点分别作出水平垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可以得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.解答下列问题:如图,抛物线顶点坐标为点C(1,4)交x轴于点A,交y轴于点B(0,3)(1)求抛物线解析式和线段AB的长度;(2)点P是抛物线(在第一象限内)上的一个动点,连接PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;(3)在第一象限内抛物线上求一点P,使S△PAB=S△CAB.法一:同底情况下,面积相等转化成平行线法二:同底情况下,面积相等转化成铅垂高相等4变式一:如图2,点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明理由.变式二:抛物线上是否存在一点P,使S△PAB=S△CAB?若存在,求出P点的坐标;若不存在,请说明5点动+面积5.如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t为何值时,PQ∥BC.(2)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在求出此时t的值;若不存在,请说明理由.(3)如图2,把△APQ沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.6形动+面积6.如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.(1)试求抛物线的解析式;(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标...