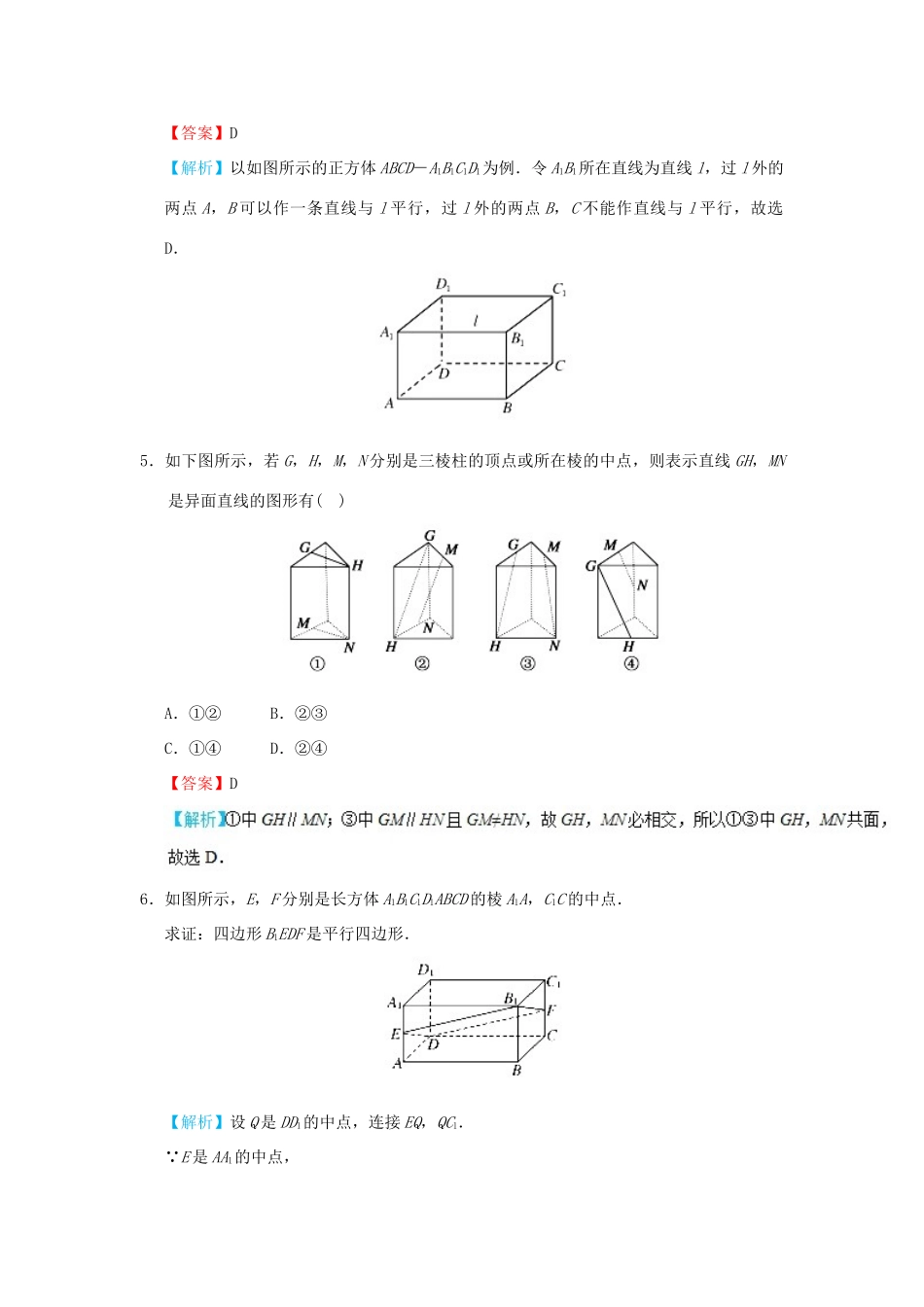
考点17空间中直线与直线的位置关系空间中的几个点或几条直线,如果都在同一平面内,我们就说它们共面,如果两条直线共面,则它们平行或相交,否则它们是异面直线.与一个平面相交于一点的直线与这个平面内不经过交点的直线是异面直线.【例】下面三个命题:①若直线a,b异面,b,c异面,则a,c异面;②若直线a,b相交,b,c相交,则a,c相交;③若直线a∥b,则a,b与c所成的角相等.其中真命题的个数为()A.3B.2C.1D.0【解题策略】反证法在立体几何的证明中应用很普遍,反证法实际上是证明命题的等价命题,要注意若命题的反面情况不止一种时,必须将其逐一否定,才能推出命题正确.1.过一点与已知直线垂直的直线有()A.一条B.两条C.无数条D.无法确定【答案】C【解析】过一点与已知直线垂直的直线有无数条,包括相交垂直和异面垂直.2.异面直线是指()A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线【答案】D【解题技巧】判定两直线的位置关系的依据就在于两直线平行、相交、异面的定义.很多情况下,定义就是一种常用的判定方法.3.若a、b是异面直线,b、c是异面直线,则()A.a∥cB.a、c是异面直线C.a、c相交D.a、c平行或相交或异面【答案】D【解析】a、b、c的位置关系有下面三种情况,如图所示,由图形分析可得答案为D.【思路小结】先判断两条直线是否有公共点,然后在没有公共点的两直线中判断是否共面,如果不共面,则两条直线异面.4.过直线l外两点可以作l的平行线条数为()A.1B.2C.3D.0或1【答案】D【解析】以如图所示的正方体ABCD-A1B1C1D1为例.令A1B1所在直线为直线l,过l外的两点A,B可以作一条直线与l平行,过l外的两点B,C不能作直线与l平行,故选D.5.如下图所示,若G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有()A.①②B.②③C.①④D.②④【答案】D6.如图所示,E,F分别是长方体A1B1C1D1ABCD的棱A1A,C1C的中点.求证:四边形B1EDF是平行四边形.【解析】设Q是DD1的中点,连接EQ,QC1.∵E是AA1的中点,∴EQ═∥A1D1.又在矩形A1B1C1D1中,A1D1═∥B1C1,∴EQ═∥B1C1(平行公理).∴四边形EQC1B1为平行四边形.∴B1E═∥C1Q.又∵Q,F是DD1,C1C两边的中点,∴QD═∥C1F.∴四边形QDFC1为平行四边形.∴C1Q═∥DF.又∵B1E═∥C1Q,∴B1E═∥DF.∴四边形B1EDF为平行四边形.1.分别和两条异面直线都相交的两条直线一定()A.异面B.相交C.不相交D.不平行【答案】D2.如图所示,在三棱锥P-ABC的六条棱所在的直线中,异面直线共有()A.1对B.2对C.3对D.4对【答案】C【解析】根据异面直线的定义可知共3对,分别为AP与BC,CP与AB,BP与AC.3.已知两条直线a,b都和第三条直线c垂直并相交,则直线a,b的位置关系是().A.平行B.相交C.异面D.平行、相交、异面【答案】D【解析】直线a,b都和第三条直线c垂直并相交,则直线a,b的关系可能平行,可能相交,也可能异面.4.已知α∩β=a,b⊂β,a∩b=A,c⊂α,且c∥a,求证:b、c为异面直线.从船和桥看直线的位置关系