高考数学解决立体几何问题思路新探VIP免费

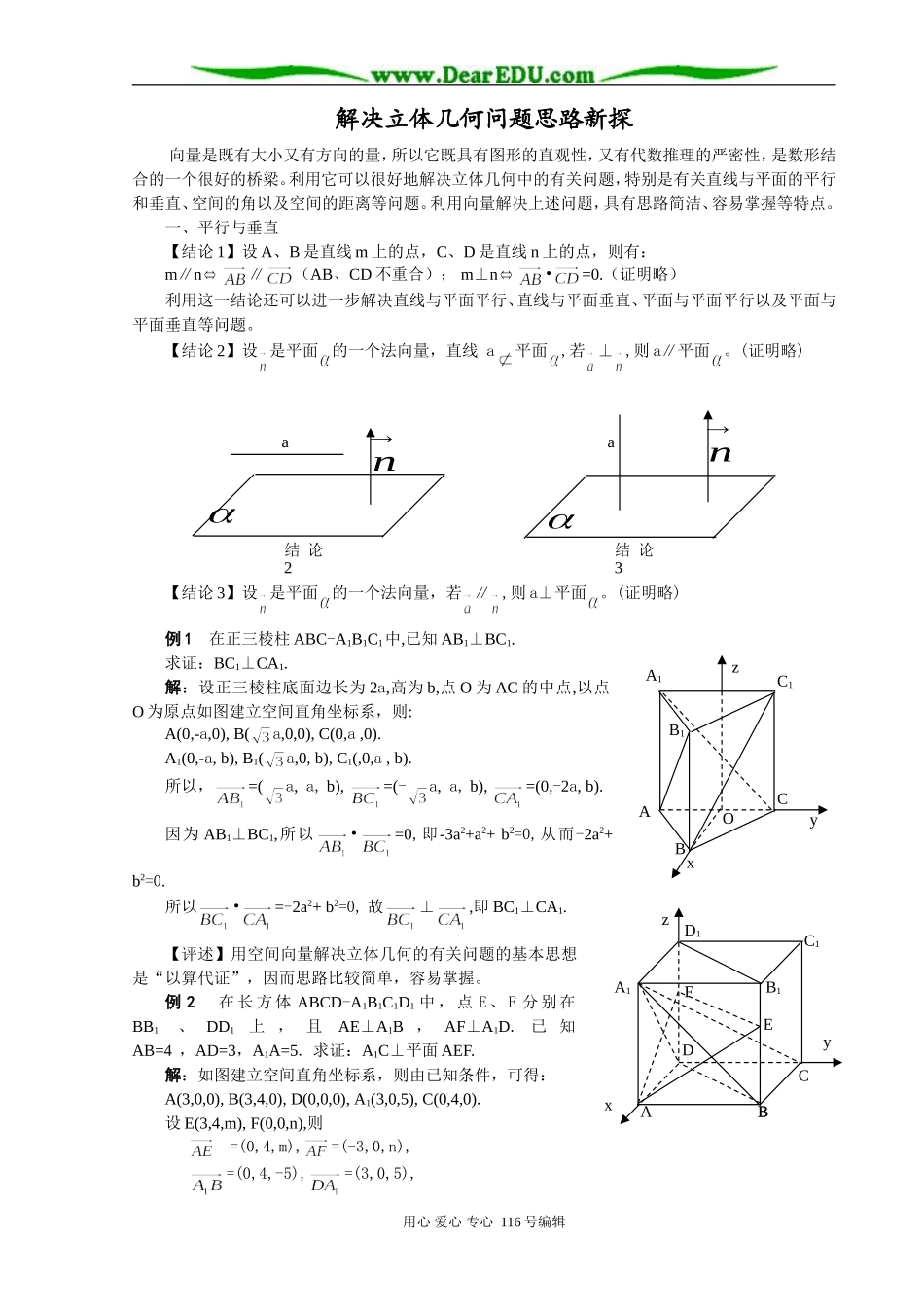
解决立体几何问题思路新探向量是既有大小又有方向的量，所以它既具有图形的直观性，又有代数推理的严密性，是数形结合的一个很好的桥梁。利用它可以很好地解决立体几何中的有关问题，特别是有关直线与平面的平行和垂直、空间的角以及空间的距离等问题。利用向量解决上述问题，具有思路简洁、容易掌握等特点。一、平行与垂直【结论1】设A、B是直线m上的点，C、D是直线n上的点，则有：m∥n∥（AB、CD不重合）；m⊥n•=0.（证明略）利用这一结论还可以进一步解决直线与平面平行、直线与平面垂直、平面与平面平行以及平面与平面垂直等问题。【结论2】设是平面的一个法向量，直线a平面,若⊥,则a∥平面。(证明略)【结论3】设是平面的一个法向量，若∥,则a⊥平面。(证明略)例1在正三棱柱ABC-A1B1C1中,已知AB1⊥BC1.求证：BC1⊥CA1.解：设正三棱柱底面边长为2a,高为b,点O为AC的中点,以点O为原点如图建立空间直角坐标系，则:A(0,-a,0),B(a,0,0),C(0,a,0).A1(0,-a,b),B1(a,0,b),C1(,0,a,b).所以，=(a,a,b),=(-a,a,b),=(0,-2a,b).因为AB1⊥BC1,所以•=0,即-3a2+a2+b2=0,从而-2a2+b2=0.所以•=-2a2+b2=0,故⊥,即BC1⊥CA1.【评述】用空间向量解决立体几何的有关问题的基本思想是“以算代证”，因而思路比较简单，容易掌握。例2在长方体ABCD-A1B1C1D1中，点E、F分别在BB1、DD1上，且AE⊥A1B，AF⊥A1D.已知AB=4，AD=3，A1A=5.求证：A1C⊥平面AEF.解：如图建立空间直角坐标系，则由已知条件，可得：A(3,0,0),B(3,4,0),D(0,0,0),A1(3,0,5),C(0,4,0).设E(3,4,m),F(0,0,n),则=(0,4,m),=(-3,0,n),=(0,4,-5),=(3,0,5),用心爱心专心116号编辑yxzAA1B1C1D1DCBEFna结论2n结论3aBACC1A1B1yxzO=(-3,4,-5).由已知得：⊥,⊥，即•=0,•=0，所以16-5m=0,-9+5n=0,解得：m=,n=.这时=(0,4,),=(-3,0,).所以•=16-16=0，•=9-9=0，即⊥，⊥，故平面AEF,即A1C⊥平面AEF.二、有关的角【结论4】设A∈a,B∈a,C∈b,D∈b,且直线a与b是异面直线，则<,>就是异面直线a与b所成的角或它的补角。（证明略）【结论5】如图，设A∈a,B∈a,是平面α的一个法向量，如果<,>是一个锐角，则直线a与平面α所成的角就是<,>的余角，即-<,>；如果<,>是一个钝角，则直线a与平面α所成的角就等于<,>-。【结论6】设α、β是二面角α-L-β的两个面，、分别是α、β的法向量，如果当与的起点都在二面角的面内,方向均指向二面角的内部或均指向二面角的外部，则这个二面角的大小就是π-<,>;如果与的方向一个指向二面角的内部，另一个指向二面角的外部，则这个二面角的大小就是<,>.例3在正四棱锥V-ABCD中,E为VC中点,正四棱锥底面边长为2，高为1.（1）求异面直线BE与VA所成的角的余弦；（2）求二面角B-VC-D的大小.解:设正四棱锥底面中心为O,以O为原点建立空间直角坐标系，其中Ox∥BC，Oy∥AB.(1)由题意得：V(0,0,1),A(1,-1,0),B(1,1,0),C(-1,1,0),D(-1,-1,0),E(-0.5，0.5,0.5).由此，得：=(-1.5,-0.5,0.5,),=(1,-1,-1).所以•=-1.5+0.5-0.5=-1.5,||=,||=.从而cos<,>=.所以异面直线BE与VA所成角的余弦为.(2)设=(x1,y1,z1),=(x2,y2,z2)分别是平面VBC与平面VCD的法向量，则⊥,⊥,⊥,⊥.用心爱心专心116号编辑xzAyBCDOVEnBAnαa而=(1,-1,1),=(-2,0,0),=(0,-2,0).所以:•=x1-y1+z1=0,•=-2x1=0,解得其中一组解为x1=0,y1=z1=1,即=(0,1,1).•=x2-y2+z2=0,•=-2y2=0,解得其中一组解为y2=0,x2=-1,z2=1,即=(-1,0,1).所以，cos<,>=.故二面角B-VC-D的大小为120°.例4正三棱柱ABC-A1B1C1的底面边长为1，侧棱长为。求AC1与侧面ABB1A1所成的角。解法1:如图，以点A为坐标原点，以AB所在直线为y轴，以AA1所在直线为z轴，以经过原点且与平面ABB1A1垂直的直线为x轴，建立空间直角坐标系。由已知得：A(0,0,0),B(0,1,0),A1(0,0,),C1(-,,).设A1B1的中点M，则:M（0，，），连结AM、MC1，于是，0，0），且，由于，所以MC1⊥平面ABB1A1。故AC1与AM所成的角就是AC1与侧面ABB1A1所成的角。所以，AC1与侧面ABB1A1所成的角为30°.解法2:同解法1建立空间直角坐标系。容易证明，=(1,0,0)是平面ABB1A1的一个法向量。而.所以而120°-90°=30°,从而AC1与侧面ABB1A1所成的角为3...