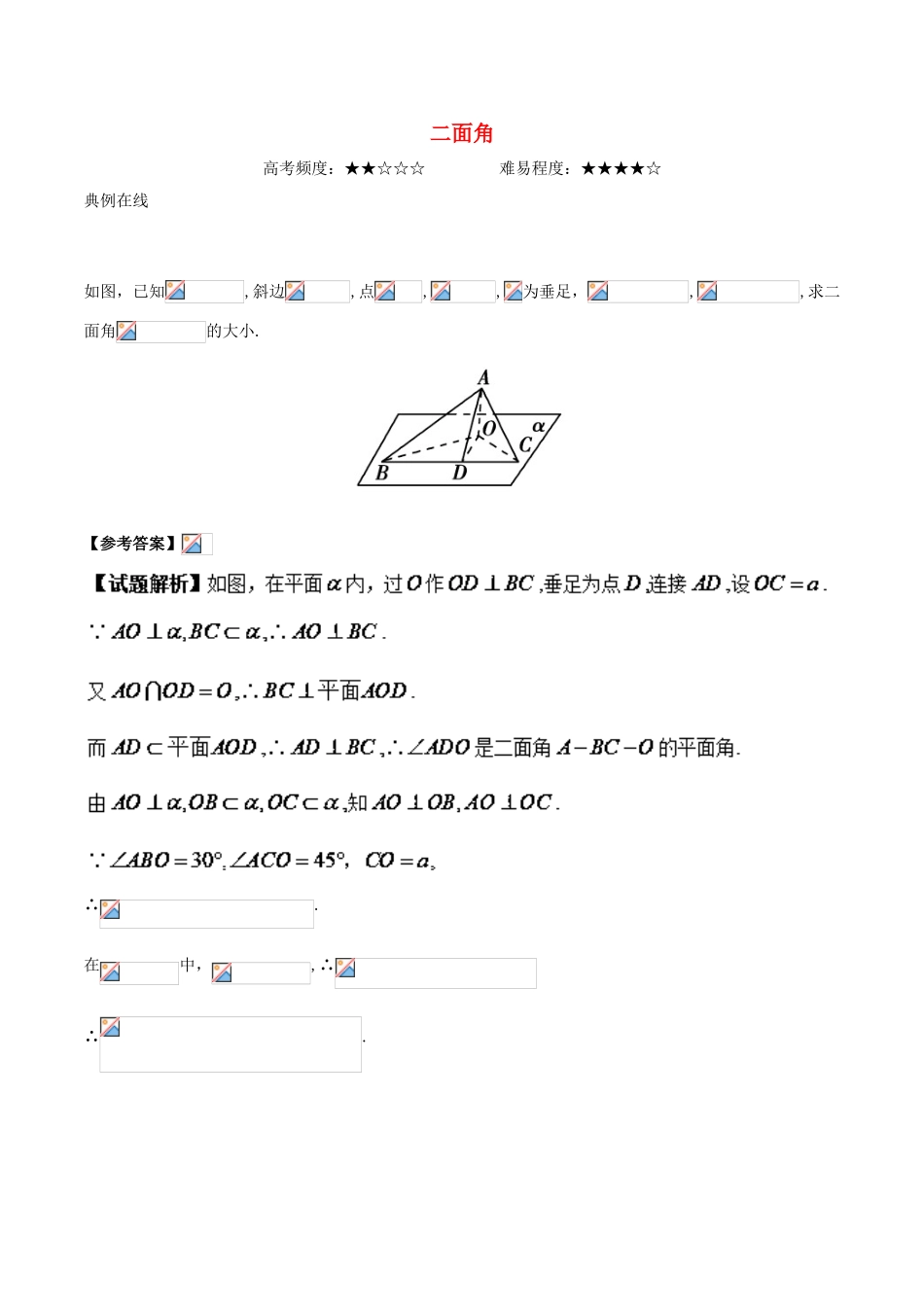
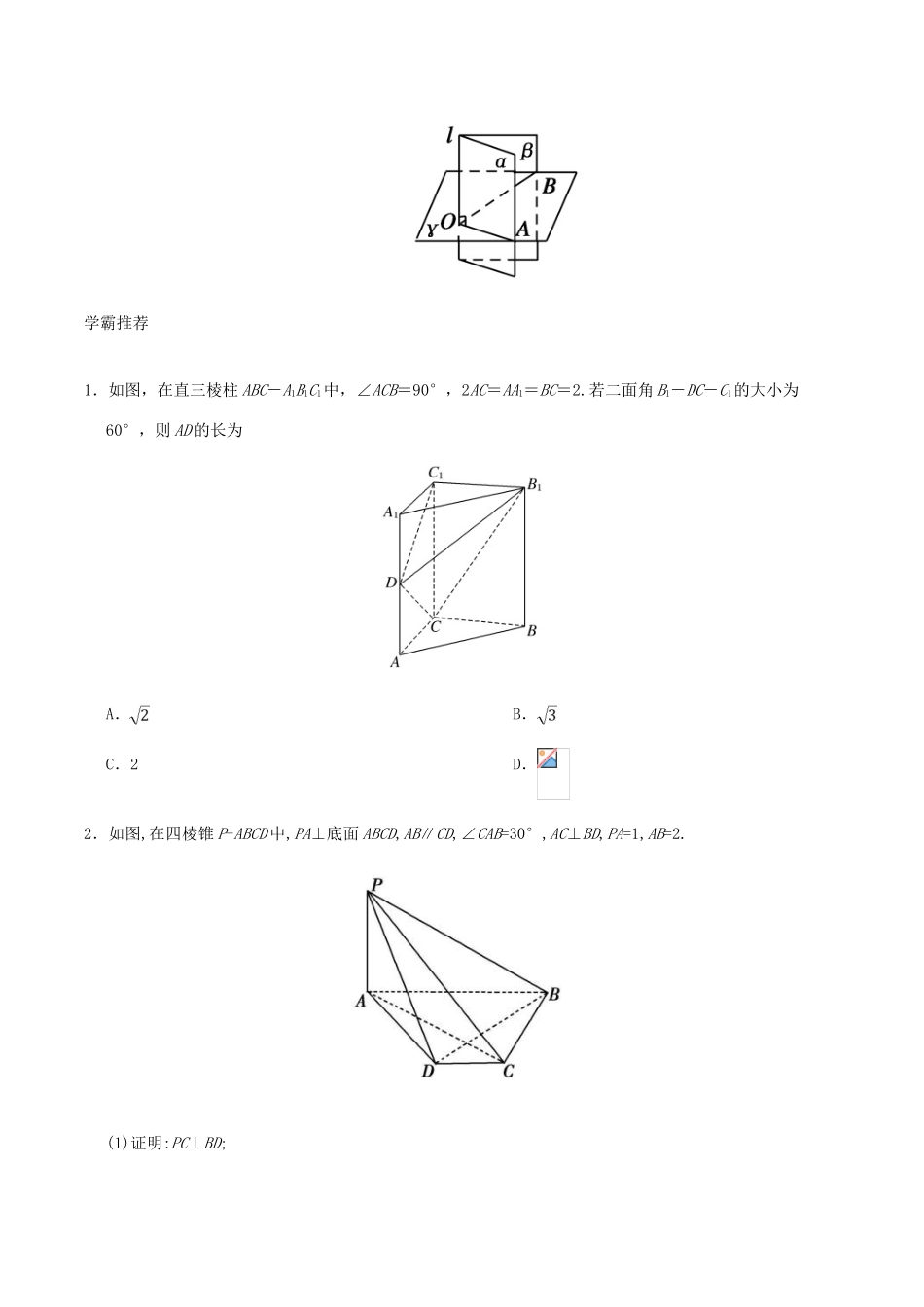
二面角高考频度:★★☆☆☆难易程度:★★★★☆典例在线如图,已知,斜边,点,,为垂足,,,求二面角的大小.【参考答案】∴.在中,,∴∴.在中,∴,即二面角的大小是.【解题必备】1.二面角的平面角的顶点是二面角棱上任意一点.为了解题方便,可以把其放在某一特殊位置,这要具体问题具体分析.2.求二面角的关键是找出(或作出)平面角,再把平面角放到三角形中求解.作二面角的平面角的方法:方法一:(定义法)在二面角的棱上找一个特殊点,在两个半平面内分别作垂直于棱的射线.如图所示,为二面角的平面角.方法二:(垂线法)过二面的一个面内一点作另一个平面的垂线,过垂足作棱的垂线,利用线面垂直可找到二面角的平面角或其补角.如图所示,为二面角的平面角.方法三:(垂面法)过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.如图所示,为二面角的平面角.学霸推荐1.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.若二面角B1-DC-C1的大小为60°,则AD的长为A.B.C.2D.2.如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠CAB=30°,AC⊥BD,PA=1,AB=2.(1)证明:PC⊥BD;(2)求二面角A-PB-D的余弦值.1.【答案】A【解析】由,知,又由直三棱柱的性质知,则平面,如图,在平面内过作,交或延长线于点,连接,由三垂线定理可知为二面角的平面角,得,由知,,设,则,由的面积为1,得,解得,即,故选A.又HK⊥PB,OH∩HK=H,∴PB⊥平面OHK,而OK⊂平面OHK,∴OK⊥PB,∴∠OKH是二面角A-PB-D的平面角.在中,AO=,OB=1,AB=2,∴OH=,HB=.易知,∴,∴HK=.在中,OK=,cos∠OKH=.∴二面角A-PB-D的余弦值为.