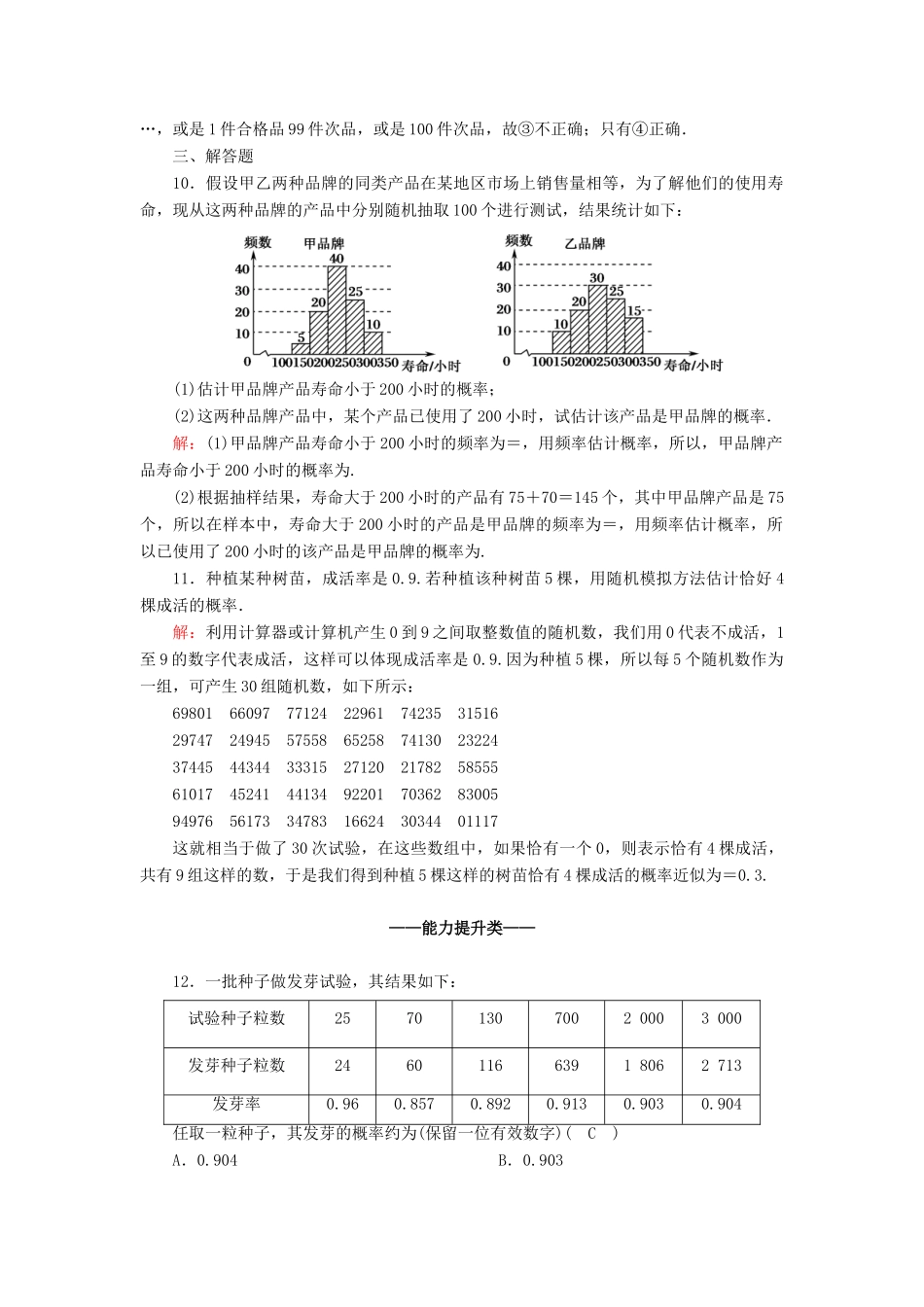
课时作业48频率与概率时间:45分钟——基础巩固类——一、选择题1.以掷一枚均匀的硬币两次为一次随机试验,收集1000次试验结果进行统计,发现事件M=“一次正面朝上,一次反面朝上”发生了501次;事件N=“至少一次正面朝上”发生748次.则下列结果正确的是(D)A.P(M)≈,P(N)≈B.P(M)≈,P(N)≈C.P(M)≈,P(N)≈D.P(M)≈,P(N)≈解析:由频率估计概率,故P(M)≈,P(N)≈.2.在n次重复进行的试验中,事件A发生的频率为,当n很大时,P(A)与的关系是(A)A.P(A)≈B.P(A)D.P(A)=解析:事件A发生的概率近似等于该频率的稳定值.3.每道选择题有4个选项,其中只有1个选项是正确的,某次考试共有12道选择题,某人说:“每个选项正确的概率是,我每题都随机地选择其中一个选项,则一定有3道选择题结果正确.”这句话(B)A.正确B.错误C.不一定正确D.以上都不对解析:虽然答对一道题的概率为,但实际问题中,并不意味着一定答对3道,可能全对,可能对3道,也可能全不对等.4.某医院治疗一种疾病的治愈率为,前4位病人都未治愈,则第5位病人的治愈率为(B)A.1B.C.D.0解析:治愈率为,表明每位病人被治愈的概率均为,并不是5人中必有1人被治愈.故选B.5.若在同等条件下进行n次重复试验得到某个事件A发生的频率f(n),则随着n的逐渐增大,有(D)A.f(n)与某个常数相等B.f(n)与某个常数的差逐渐减小C.f(n)与某个常数的差的绝对值逐渐减小D.f(n)在某个常数的附近摆动并趋于稳定解析:对于一个事件而言,概率是一个常数,而频率则随着试验次数的变化而变化,试验次数越多,频率就越接近于事件的概率,但并不是试验次数越多,所得频率就一定更接近于概率值.6.(多选)投掷一枚普通的正方体骰子,四位同学各自发表了以下见解,其中正确的见解有(AD)A.出现“点数为奇数”的概率等于出现“点数为偶数”的概率B.只要连掷6次,一定会“出现1点”C.投掷前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大D.连续投掷3次,出现的点数之和不可能等于19解析:A:掷一枚骰子,出现奇数点和出现偶数点的概率都是,故A正确;B:“出现1点”是随机事件,故B错误;C:概率是客观存在的,不因为人的意念而改变,故C错误;D:连续掷3次,每次都出现最大点数6,则三次之和为18,故D正确.二、填空题7.对某厂生产的某产品进行抽样检查,数据如下表所示:抽查件数50100200300500合格件数4792192285478根据表中所提供的数据,若要从该厂生产的此种产品抽到950件合格品,大约需抽查1_000件产品.解析:由题表中数据知:抽查5次,产品合格的频率依次为0.94,0.92,0.96,0.95,0.956,可见频率在0.95附近摆动,故可估计该厂生产的此种产品合格的概率约为0.95.设大约需抽查n件产品,则≈0.95,所以n≈1000.8.给出下列四个命题:①设有一批产品,其次品率为0.05,则从中任取200件,必有10件是次品;②做100次抛硬币的试验,结果51次出现正面朝上,因此,出现正面朝上的概率是;③随机事件发生的频率就是这个随机事件发生的概率;④抛掷骰子100次,得点数是1的结果有18次,则出现1点的频率是.其中正确命题有④.解析:①错,次品率是大量产品的估计值,并不是针对200件产品来说的.②③混淆了频率与概率的区别.④正确.9.已知某产品的次品率为1%,有下列四种说法:①从产品中任取100件,其中一定有1件次品;②从产品中依次抽取100件产品,若前面99件均为合格品,则第100件一定为次品;③从产品中任意抽取100件,则这100件产品不可能全为合格品;④从产品中任取一件,为次品的可能性为1%.其中正确的是④.解析:因为次品率即出现次品的概率,次品率为1%,是指产品为次品的可能性为1%,所以从产品中任意抽取100件,其中可能有1件次品,而不是一定有1件次品,①不正确;随机事件每次发生的概率是相等的,并不受前后试验的影响,故第100件产品为次品的可能性仍为1%,②不正确;抽100件产品相当于做100次试验,因为每次试验结果都是随机的,也就是每次抽取可能抽到合格品也可能抽到次品,事实上,这100件产品有101种可能,即可能是100件合格品,也可能是99件合格品1件次品,或是98件合格品2件次...