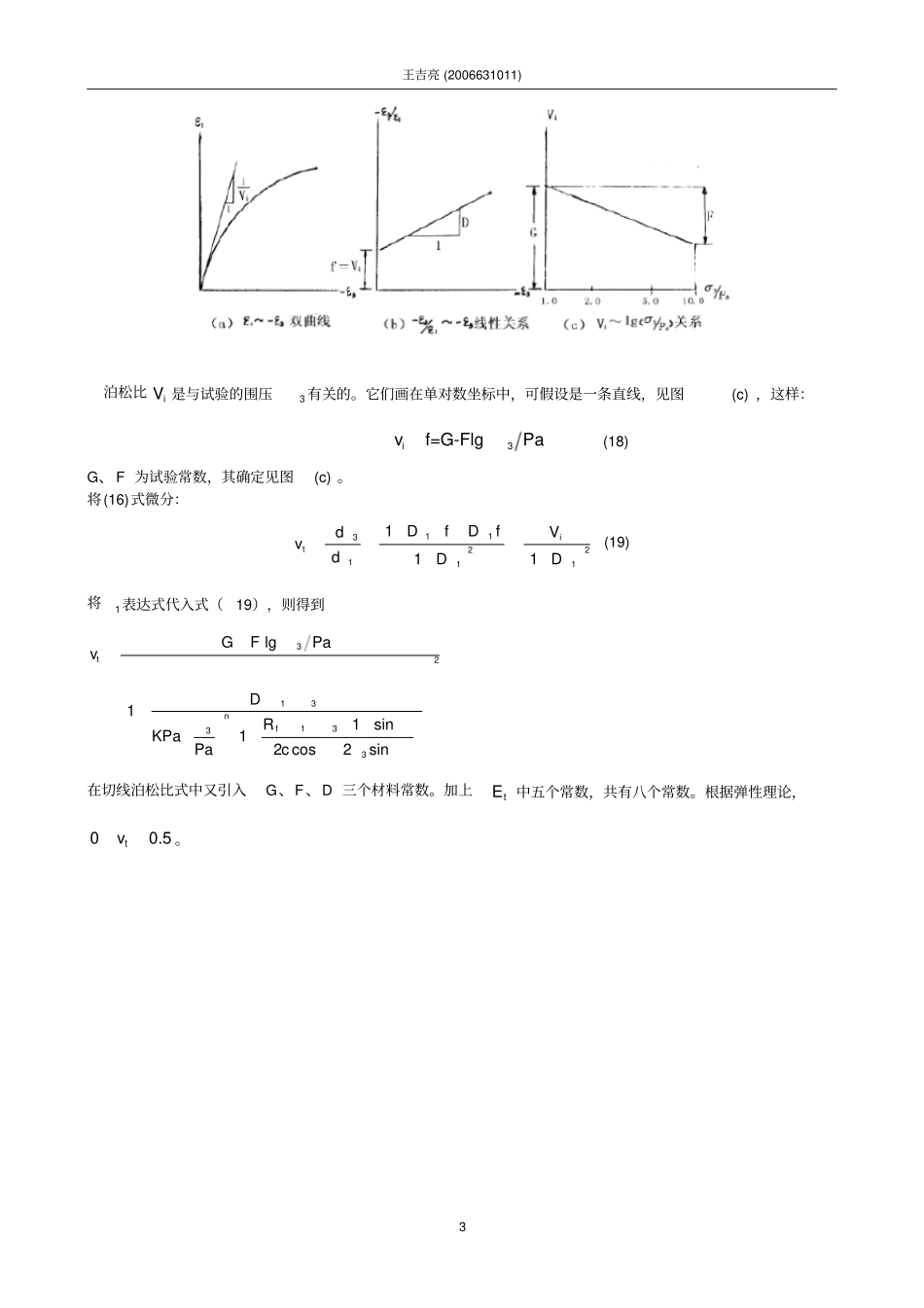
邓肯-张模型是一个非线性本构模型,既然是一个本构模型,可想而之他反应的是应力与应变之间的关系。说它是非线性的,那么反映应力应变关系的模量就不是一个常数E那么简单。在介绍该模型之前,先要介绍一个概念,就是反映非线性关系的增量广义胡克定律:1123()tttvddddEE(1)1963年,康纳(Kondner)根据大量土的三轴试验的应力应变关系曲线,提出可以用双曲线拟合出一般土的三轴试验13()~a曲线,即:13aaab(2)其中,a、b为试验常数。对于常规三轴压缩试验,1a。邓肯等人根据这一双曲线应力应变关系提出了一种目前被广泛的增量弹性模型,一般被称为邓肯-张(Duncan-Chang)模型。在常规三轴压缩试验中,13aaab可以写成:1113ab(3)将常规三轴压缩试验的结果按1113~的关系进行整理,则二者近似成线性关系(见图1)。其中,a为直线的截距;b为直线的斜率。在常规三轴压缩试验中,由于230dd,所以切线模量为ε1/(σ1-σ3)1b=1/(σ1-σ3)ulta=1/Ei图11113~线性关系图13211()()tdaEdab(4)在试验的起始点,10,tiEE,则:1iEa,这表明a表示的是在这个试验中的起始变形模量Ei的倒数。如果1,则:131()ultb(5)由此可以看出b代表的是双曲线的渐近线所对应的极限偏差应力13()ult的倒数。在土的试样中,如果应力应变曲线近似于双曲线关系,则往往是根据一定的应变值(如115%)来确定土的强度13()f,而不可能在试验中使1无限大,求取13()ult;对于有峰值点的情况,取1313()()f峰,这样1313()()fult<。定义破坏比Rf为:1313()()ffRult(6)而13131()()ffRbult(7)将上式与1iEa代入13211()()tdaEdab(8)得到:塑性力学读书报告22113111()tfiiEREE(9)该式表示为应变1的函数,使用时不方便,可将tE表示为应力的函数形式。由式1113ab(10)可以得到13113()1()ab,将该式代入13211()()tdaEdab得到221313131()1[][]1()1()taEabaabb将式13131()()ffRbult和1iEa代入上式得到:21313[1]()tiifEER(11)根据莫尔-库仑强度准则,有3132cos2sin()1sinfc(12)如果绘制lg(/)iaEP与3lg(/)aP的关系图,可以发现二者近似呈直线关系,所以得式:3()niaaEKPP(13)其中,aP为大气压(aP=101.4kaP),量纲与3相同;K、n为试验常数,分别代表lg(/)iaEP与3lg(/)aP直线的截距和斜率。将3132cos2sin()1sinfc(14)和3()niaaEKPP代入21313[1]()tiifEER,则得到:13233()(1sin)()[1]2cos2sinfntaaREKPPc(15)可见切线变形模量中包括5个材料常数K、n、、c、fR。2切线泊松比(poisson'sratio)Duncan等人根据一些试验资料,假定在常规三轴压缩试验中轴向应变1与侧向应变3之间也存在双曲线关系313fD(16)或者3331fDfD(17)从上式,试验得到的31与3的关系可近似为直线关系,从而确定截距f与斜率D。从式上式可见当30时,310ifViV即为初始泊松比。见图(a)。D为13:关系渐近线的倒数,见图(b)。试验表明土的切线王吉亮(2006631011)3泊松比iV是与试验的围压3有关的。它们画在单对数坐标中,可假设是一条直线,见图(c),这样:3f=G-FlgPaiv(18)G、F为试验常数,其确定见图(c)。将(16)式微分:11322111111itDfDfdVvdDD(19)将1表达式代入式(19),则得到32131333lg11sin12cos2sintnfGFPavDRKPaPac在切线泊松比式中又引入G、F、D三个材料常数。加上tE中五个常数,共有八个常数。根据弹性理论,00.5tv。