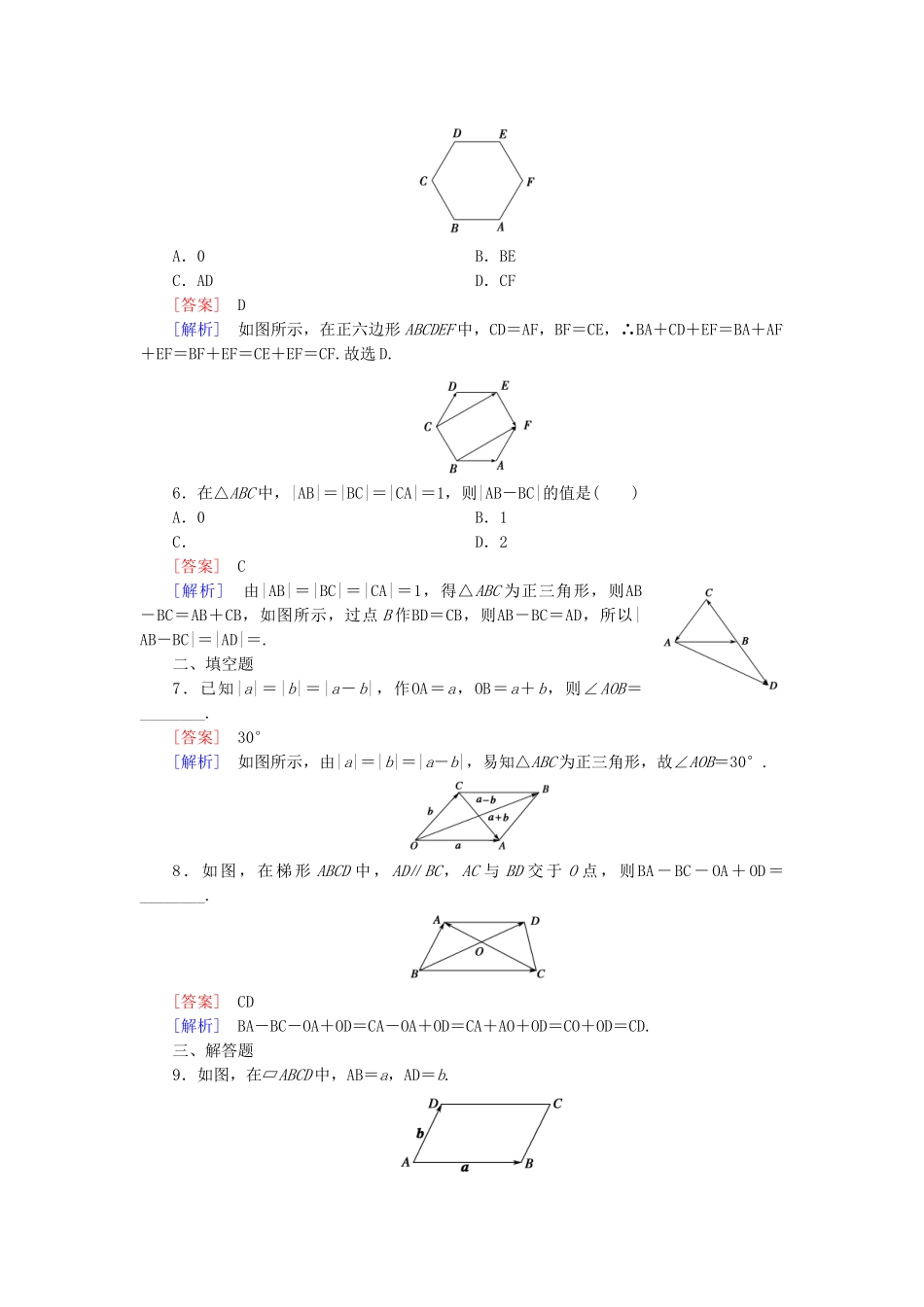
【成才之路】-学年高中数学2.2从位移的合成到向量的加法基础巩固北师大版必修4一、选择题1.化简OP+PQ+PS+SP的结果等于()A.QPB.OQC.SPD.SQ[答案]B[解析]原式=(OP+PQ)+(PS+SP)=OQ+0=OQ.2.设(AB+CD)+(BC+DA)=a,而b是一个非零向量,则在下列各结论中,正确的结论为()①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|.A.①②B.③④C.②④D.①③[答案]D[解析]由向量加法的交换律、结合律及三角形法则,得a=0,由向量的性质可知②④错误,①③正确.3.若O,E,F是不共线的任意三点,则以下各式成立的是()A.EF=OF+OEB.EF+OE=OFC.EF=FO+OED.EF=FO+EO[答案]B[解析]可以画出图形,然后利用三角形法则找出正确答案.如图,由图知选项A,D不正确;FO+OE=FE,故选项C不正确;EF+OE=OE+EF=OF,故选项B正确,故选B.4.下列命题中,真命题的个数为()①若a+b与a-b是共线向量,则a与b也是共线向量;②若|a|-|b|=|a-b|,则a与b是共线向量;③若|a-b|=|a|+|b|,则a与b是共线向量;④若||a|-|b||=|a|+|b|,则b与任何向量都共线.A.1个B.2个C.3个D.4个[答案]C[解析]要选出正确答案,需对每个命题进行判断.若a与b不共线,则由向量加法和减法的几何意义知a+b与a-b分别是以a,b为邻边的平行四边形的两条对角线,因此a+b与a-b不共线,与已知条件矛盾,从而a与b必为共线向量,故命题①正确;由不等式||a|-|b||≤|a-b|≤|a|+|b|中等号成立的条件可知命题②与③都正确;由||a|-|b||=|a|+|b|可得|a|-|b|=|a|+|b|或|a|-|b|=-|a|-|b|,所以|b|=0或|a|=0,从而b=0或a=0,即说明b不一定为零向量,故命题④不正确,故选C.5.如图所示,正六边形ABCDEF中,BA+CD+EF等于()A.0B.BEC.ADD.CF[答案]D[解析]如图所示,在正六边形ABCDEF中,CD=AF,BF=CE,∴BA+CD+EF=BA+AF+EF=BF+EF=CE+EF=CF.故选D.6.在△ABC中,|AB|=|BC|=|CA|=1,则|AB-BC|的值是()A.0B.1C.D.2[答案]C[解析]由|AB|=|BC|=|CA|=1,得△ABC为正三角形,则AB-BC=AB+CB,如图所示,过点B作BD=CB,则AB-BC=AD,所以|AB-BC|=|AD|=.二、填空题7.已知|a|=|b|=|a-b|,作OA=a,OB=a+b,则∠AOB=________.[答案]30°[解析]如图所示,由|a|=|b|=|a-b|,易知△ABC为正三角形,故∠AOB=30°.8.如图,在梯形ABCD中,AD∥BC,AC与BD交于O点,则BA-BC-OA+OD=________.[答案]CD[解析]BA-BC-OA+OD=CA-OA+OD=CA+AO+OD=CO+OD=CD.三、解答题9.如图,在▱ABCD中,AB=a,AD=b.(1)用a,b表示AC,DB;(2)当a,b满足什么条件时,a+b与a-b所在直线互相垂直?(3)当a,b满足什么条件时,|a+b|=|a-b|;(4)a+b与a-b有可能为相等向量吗?为什么?[解析](1)AC=AB+AD=a+b,DB=AB-AD=a-b.(2)由(1)知,a+b=AC,a-b=DB,a+b与a-b所在直线垂直,即AC⊥BD,又 四边形ABCD为平行四边形,∴四边形ABCD为菱形,即a,b应满足|a|=|b|.(3)|a+b|=|a-b|,即|AC|=|BD|. 矩形的对角线相等,∴当a与b垂直时,满足|a+b|=|a-b|.(4)不可能.因为▱ABCD的两对角线不可能平行,因此a+b与a-b不可能为共线向量,那么就不可能为相等向量了.一、选择题1.在平面上有不共线的A、B、C三点,设m=AB+BC,n=AB-BC,若m与n长度恰好相等,则有()A.△ABC必为正三角形B.△ABC必为直角三角形且∠B为直角C.△ABC必为直角三角形且∠C为直角D.△ABC必为等腰直角三角形[答案]B[解析]m=AB+BC=AC,n=AB-BC=AB+CB,画出示意图,由三角形法则及三角形性质可得△ABC为直角三角形,且∠B为直角.2.如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则()A.AD+BE+CF=0B.BD-CF+DF=0C.AD+CE-CF=0D.BD-BE-FC=0[答案]A[解析] AD=AB,BE=BC,CF=CA,∴AD+BE+CF=(AB+BC+CA)=(AC+CA)=0.故选A.二、填空题3.如图,在▱ABCD中,(1)AB+________=AC;(2)AC+CD+________=AO;(3)AB+AD+CD=________;(4)________+BA+DA=0.[答案](1)AD或BC(2)DO或OB(3)AD(4)AC[解析](1) AC-AB=BC=AD,∴AB+BC=AB+AD...