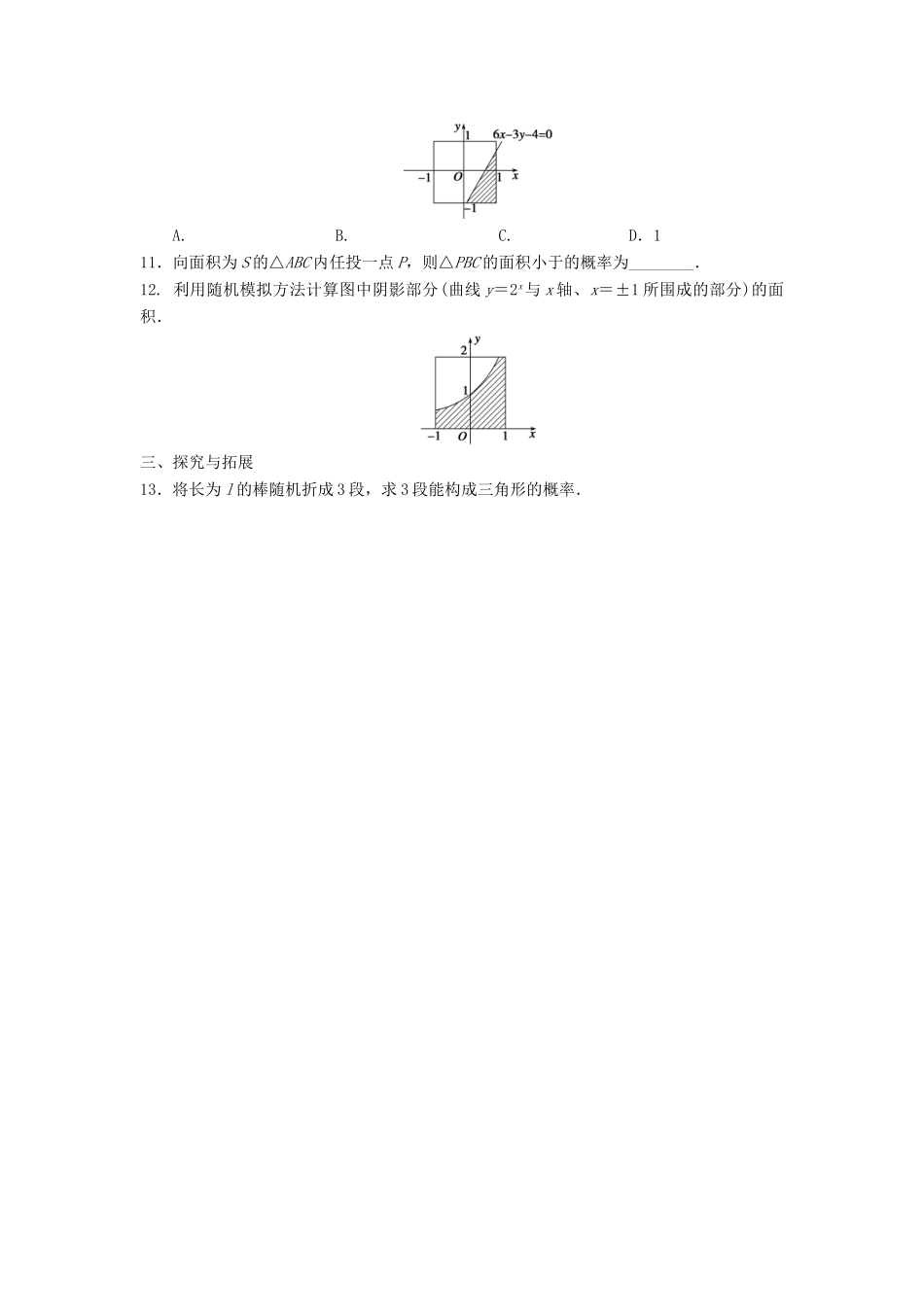
3.3.2均匀随机数的产生一、基础过关1.用计算器或计算机产生20个[0,1]之间的随机数x,但是基本事件都在区间[-1,3]上,则需要经过的线性变换是()A.y=3x-1B.y=3x+1C.y=4x+1D.y=4x-12.与均匀随机数特点不符的是()A.它是[0,1]内的任何一个实数B.它是一个随机数C.出现的每一个实数都是等可能的D.是随机数的平均数3.质点在数轴上的区间[0,2]上运动,假定质点出现在该区间各点处的概率相等,那么质点落在区间[0,1]上的概率为()A.B.C.D.以上都不对4.一海豚在水池中自由游弋,水池为长30m,宽20m的长方形,海豚离岸边不超过2m的概率为(注:海豚所占区域忽略不计)()A.B.C.D.5.方程x2+x+n=0(n∈(0,1))有实根的概率为________.6.已知右图所示的矩形,其长为12,宽为5.在矩形内随机地撒1000颗黄豆,数得落在阴影部分的黄豆数为550颗,则可以估计出阴影部分的面积约为________.7.取一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于1m的概率?(用模拟的方法求解)8.甲、乙两人约定6时到7时之间在某处会面,并约定先到者应等候另一人一刻钟,过时即可离去,请用随机模拟法估算两人能会面的概率.二、能力提升9.如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积约为()A.B.C.D.无法计算10.向图中所示正方形内随机地投掷飞镖,则飞镖落在阴影部分的概率为()A.B.C.D.111.向面积为S的△ABC内任投一点P,则△PBC的面积小于的概率为________.12.利用随机模拟方法计算图中阴影部分(曲线y=2x与x轴、x=±1所围成的部分)的面积.三、探究与拓展13.将长为l的棒随机折成3段,求3段能构成三角形的概率.答案1.D2.D3.C4.C5.6.337.解方法一(1)利用计算器或计算机产生一组0到1区间的均匀随机数a1=RAND.(2)经过伸缩变换,a=a1]N1,N)即为概率P(A)的近似值.方法二做一个带有指针的圆盘,把圆周三等分,标上刻度[0,3](这里3和0重合).转动圆盘记下指针在[1,2](表示剪断绳子位置在[1,2]范围内)的次数N1及试验总次数N,则fn(A)=即为概率P(A)的近似值.8.解设事件A={两人能会面}.(1)利用计算器或计算机产生两组0到1区间的均匀随机数,x1=RAND,y1=RAND;(2)经过伸缩变换,x=x1]N1,N),即为概率P(A)的近似值.9.B10.C11.12.解(1)利用计算机产生两组[0,1]区间上的均匀随机数,a1=RAND,b1=RAND;(2)进行平移和伸缩变换得到一组[-1,1]区间上的均匀随机数和一组[0,2]区间上的均匀随机数;(3)统计试验总次数N和落在阴影内的点数N1(满足条件b<2a的点(a,b)的个数);(4)计算频率,即落在阴影部分的概率的近似值;(5)设阴影面积为S,则用几何概型公式求得点落在阴影部分的概率为P=.≈所以,所以S≈即为阴影部分面积的近似值.13.解设A“=3”段能构成三角形,x,y分别表示其中两段的长度,则第3段的长度为l-x-y.则试验的全部结果可构成集合Ω={(x,y)|0l-x-y⇒x+y>,x+l-x-y>y⇒y<,y+l-x-y>x⇒x<.故所求结果构成集合A=.由图可知,所求概率为P(A)===.