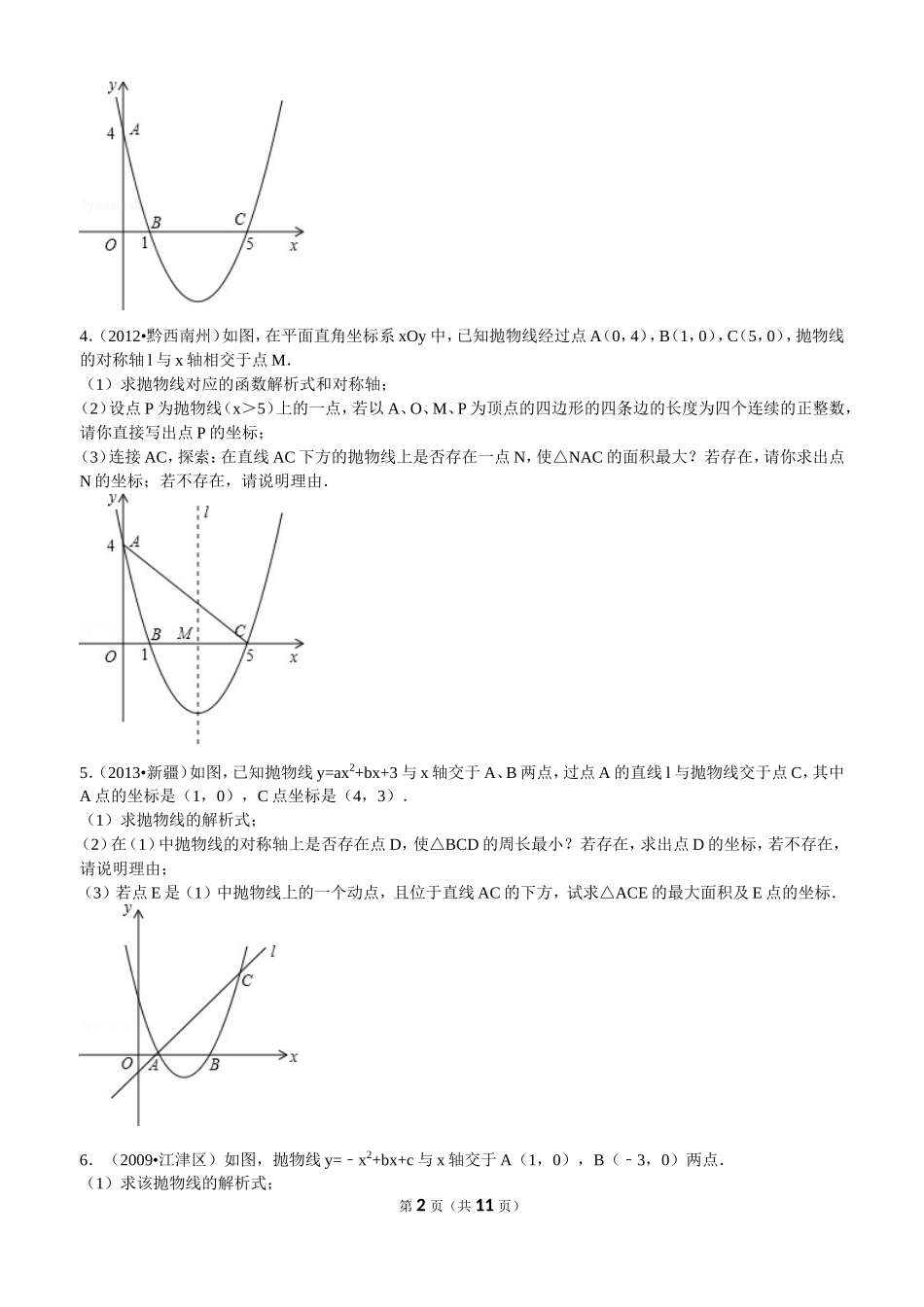
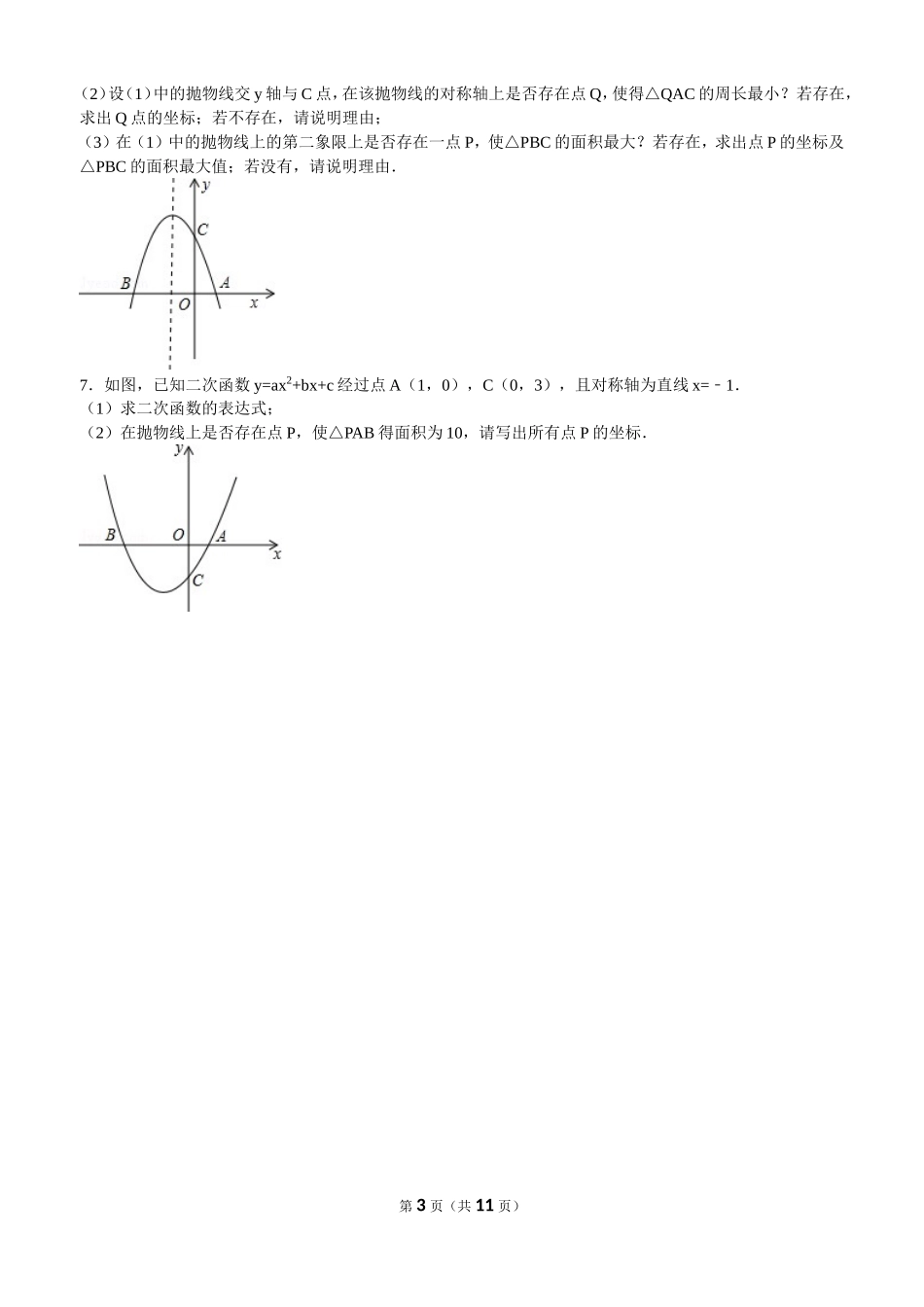
二次函数与三角形最大面积的3种求法一.解答题(共7小题)1.(2012•广西)已知抛物线y=ax2+2x+c的图象与x轴交于点A(3,0)和点C,与y轴交于点B(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点D,使得点D到点B、C的距离之和最小,并求出点D的坐标;(3)在第一象限的抛物线上,是否存在一点P,使得△ABP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.2.(2013•茂名)如图,抛物线与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).(1)求a的值和抛物线的顶点坐标;(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;(3)设N是抛物线对称轴上的一个动点,d=|ANCN|﹣.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.3.(2011•茂名)如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)点P在抛物线上,且以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由.第1页(共11页)4.(2012•黔西南州)如图,在平面直角坐标系xOy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线的对称轴l与x轴相交于点M.(1)求抛物线对应的函数解析式和对称轴;(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数,请你直接写出点P的坐标;(3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请说明理由.5.(2013•新疆)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).(1)求抛物线的解析式;(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.6.(2009•江津区)如图,抛物线y=x﹣2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.(1)求该抛物线的解析式;第2页(共11页)(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.7.如图,已知二次函数y=ax2+bx+c经过点A(1,0),C(0,3),且对称轴为直线x=1﹣.(1)求二次函数的表达式;(2)在抛物线上是否存在点P,使△PAB得面积为10,请写出所有点P的坐标.第3页(共11页)二次函数与三角形最大面积的3种求法参考答案与试题解析一.解答题(共7小题)1.(2012•广西)解答:解:(1) 抛物线y=ax2+2x+c的图象经过点A(3,0)和点B(0,3),∴,解得a=1﹣,c=3,∴抛物线的解析式为:y=x﹣2+2x+3.(2)对称轴为x==1,令y=x﹣2+2x+3=0,解得x1=3,x2=1﹣,∴C(﹣1,0).如图1所示,连接AB,与对称轴x=1的交点即为所求之D点,由于A、C两点关于对称轴对称,则此时DB+DC=DB+DA=AB最小.设直线AB的解析式为y=kx+b,由A(3,0)、B(0,3)可得:,解得k=1﹣,b=3,∴直线AB解析式为y=x+3﹣.当x=1时,y=2,∴D点坐标为(1,2).(3)结论:存在.如图2所示,设P(x,y)是第一象限的抛物线上一点,过点P作PNx⊥轴于点N,则ON=x,PN=y,AN=OAON=3x﹣﹣.SABP△=S梯形PNOB+SPNA△S﹣AOB△=(OB+PN)•ON+PN•AN﹣OA•OB=(3+y)•x+y•(3x﹣)﹣×3×3=(x+y)﹣,P (x,y)在抛物线上,∴y=x﹣2+2x+3,代入上式得:SABP△=(x+y)﹣=﹣(x23x﹣)=﹣(x﹣)2+,∴当x=时,SABP△取得最大值.当x=时,y=x﹣2+2x+3=,∴P(,)....