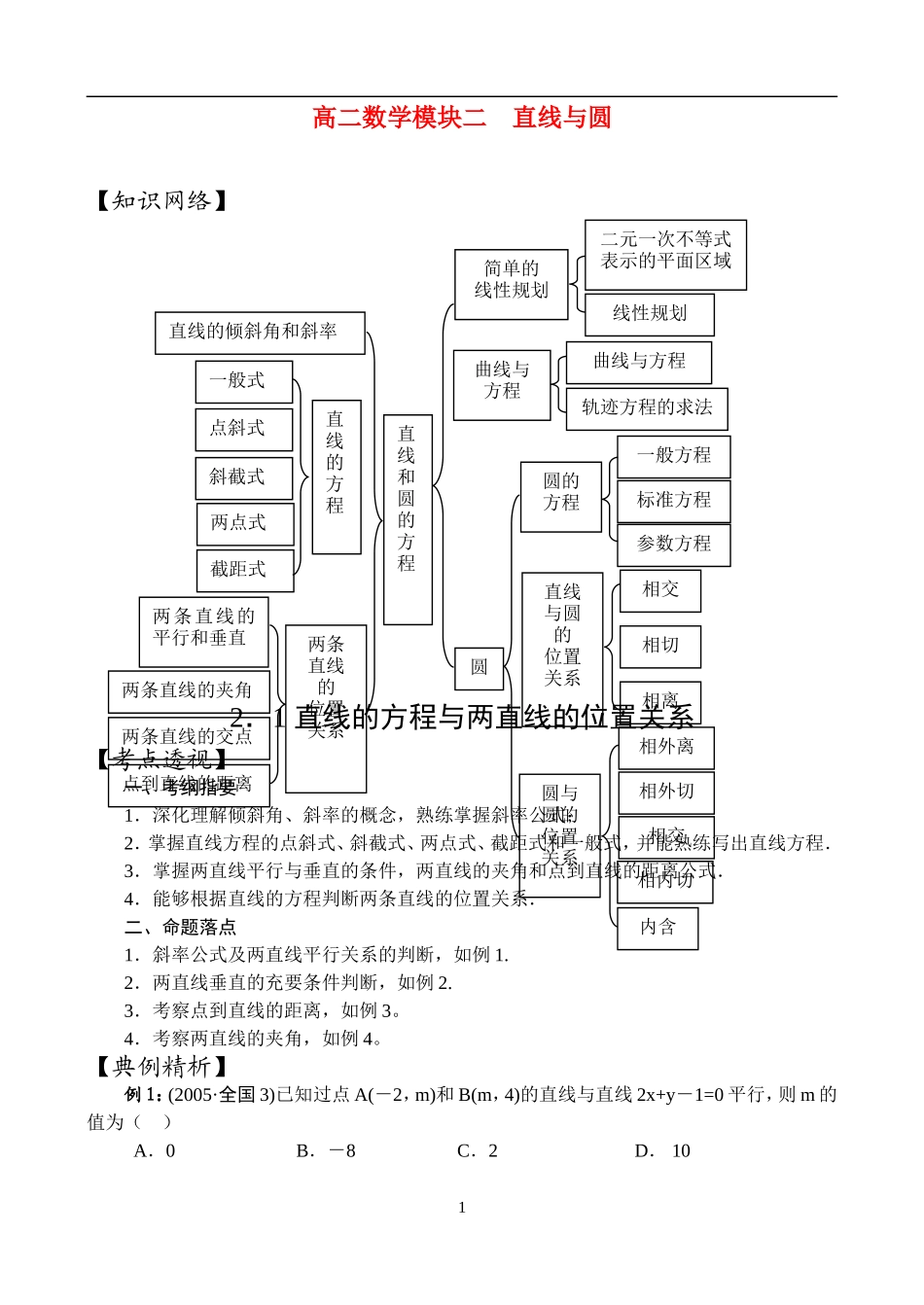
二元一次不等式表示的平面区域简单的线性规划线性规划曲线与方程曲线与方程轨迹方程的求法圆的方程一般方程标准方程参数方程圆直线与圆的位置关系相交相切相离圆与圆的位置关系相外离相外切相交相内切内含直线和圆的方程直线的倾斜角和斜率直线的方程一般式点斜式斜截式两点式截距式两条直线的位置关系两条直线的平行和垂直两条直线的夹角两条直线的交点点到直线的距离高二数学模块二直线与圆【知识网络】2.1直线的方程与两直线的位置关系【考点透视】一、考纲指要1.深化理解倾斜角、斜率的概念,熟练掌握斜率公式;2.掌握直线方程的点斜式、斜截式、两点式、截距式和一般式,并能熟练写出直线方程.3.掌握两直线平行与垂直的条件,两直线的夹角和点到直线的距离公式.4.能够根据直线的方程判断两条直线的位置关系.二、命题落点1.斜率公式及两直线平行关系的判断,如例1.2.两直线垂直的充要条件判断,如例2.3.考察点到直线的距离,如例3。4.考察两直线的夹角,如例4。【典例精析】例1:(2005·全国3)已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为()A.0B.-8C.2D.101解析: ,直线2x+y-1=0的斜率为,所以由得.答案:B例2:(2005·北京)“m=”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的()A.充分必要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件解析:当时,两直线斜率乘积为,从而可得两直线垂直,当时两直线一条斜率为0一条斜率不存在,但两直线仍然垂直.因此是题目中给出的两条直线垂直的充分但不必要条件.答案:B例3:(2004全国II,理8)在坐标平面内,与点A(1,2)的距离为1,且与点B(3,1)的距离为2的直线共有()A.1条B.2条C.3条D.4条解析:由于|AB|=<3,所以以A、B为圆心,1、2为半径的两圆一定相交,其外公切线共有两条.答案:B【常见误区】1.例2中,对于两条直线垂直的充要条件①都存在时,;②中有一个不存在另一个为零,对于②这种情况多数考生容易忽略.2.考查直线的方程,对称问题以及解析法等基础知识和基本技能.此问题在求解策略的选择上同学们常存在一定的误区,解题方法不优化.求直线的轴对称方程的方法很多,一类是利用对称性,通过夹角相等,点对称,求出直线l2的斜率或直线l2上某一点的坐标,进而求出直线l2的方程;一类是利用对称轴l的特殊性,利用特殊结论处理(特殊问题常用此法,如例4解法二).【基础演练】1.(2005·浙江)点(1,-1)到直线x-y+1=0的距离是()A.B.C.D.2.(2004全国II,文8)已知点A(1,2),B(3,1),则线段AB的垂直平分线的方程为()A.4x+2y=5B.4x-2y=5C.x+2y=5D.x-2y=53.(2004浙江,文2)直线y=2与直线x+y-2=0的夹角是()A.B.C.D.4.(2004湖北,文2)已知点M1(6,2)和M2(1,7),直线y=mx-7与线段M1M2的交点M分有向线段M1M2的比为3:2,则m的值为()2A.-B.-C.D.45.(2005·天津)在直角坐标系xOy中,已知点A(0,1)和点B(-3,4),若点C在∠AOB的平分线上且||=2,则=.6.(2004/4·黄冈)直线的倾斜角的范围是.7.(2002·全国,文21)已知点到两定点、距离的比为,点到直线的距离为1,求直线的方程.8.已知直线的方程为,过点作直线,交轴于点,交于点,且,求的方程.9.求过点且被两直线:,:所截得的线段长为的直线的方程.2.2简单的线性规划【考点透视】一、考纲指要1.了解用二元一次不等式表示平面区域,了解线性规划的意义,并会简单的应用;2.通过以线性规划为内容的研究课题与实习作业,提高解决实际问题的能力.二、命题落点1.作出不等式所确定的可行域,并求其面积,考察分类讨论思想,如例1;2.线性规划知识的应用.线性规划与实际生活中求最优解问题十分密切,很能体现用数学知识解决实际问题的思路,复习中应该加以重视,如例2;3.解析几何的综合题型,在高考试题中解析几何经常会与函数、数列、不等式、向量等综合考查各种数学思想及方法,如例3.【典例精析】例1:(2005·全国1)在坐标平面上,不等式组所表示的平面区域的面积为()A.B.C.D.2解析:原不等式化为或,所表示的平面区域如右图所示,,,3yxO111AB∴,故选B.答案:B.例2:(2005·山...