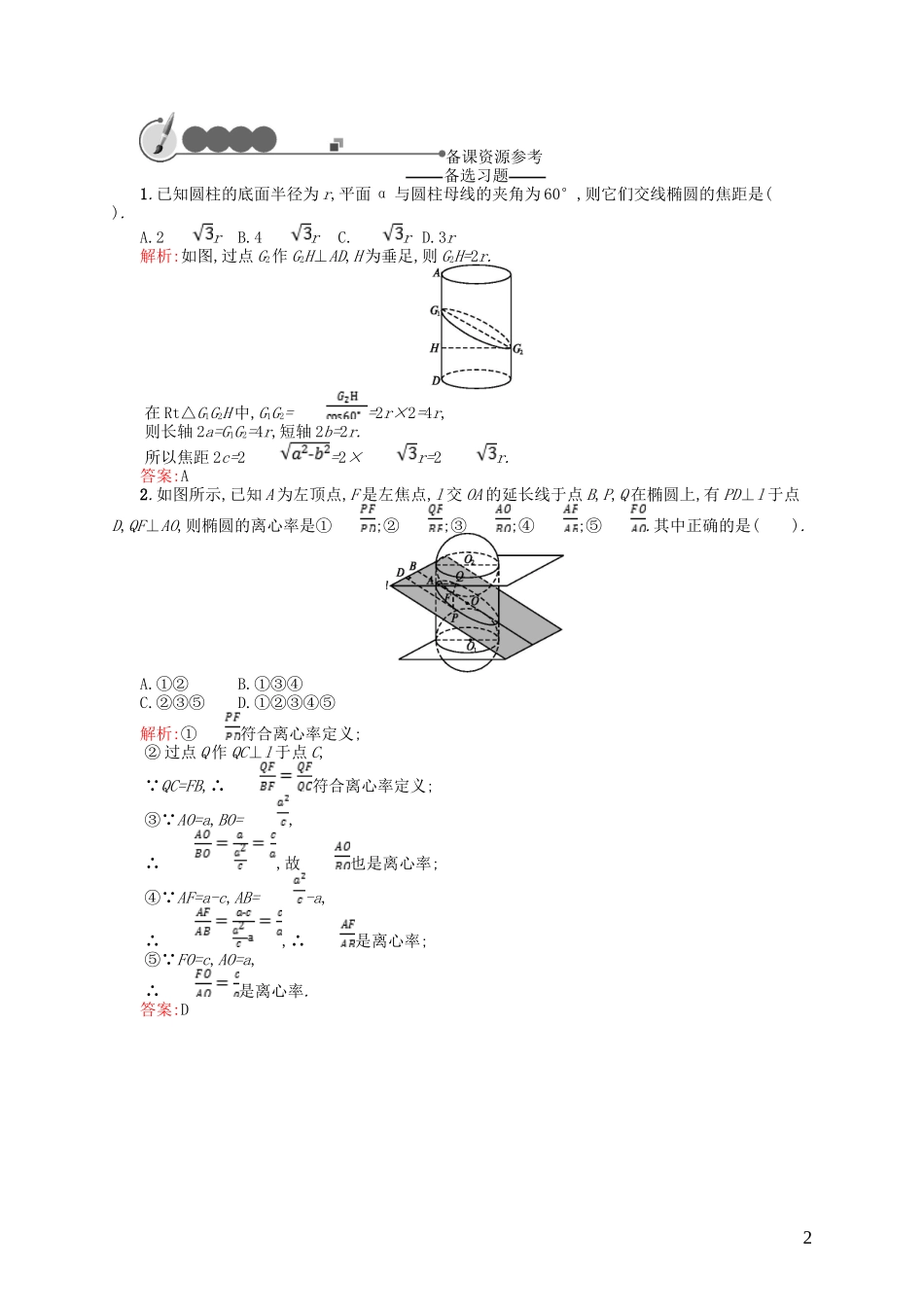
§3柱面与平面的截面课后作业提升1椭圆的长轴长为10,短轴长为8,则焦距等于().A.6B.8C.10D.3解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c,则由题意知2a=10,2b=8,故a=5,b=4,∴2c=2=6.答案:A2一组底面为同心圆的圆柱面被一平面所截,则交线椭圆具有().A.相同的长轴B.相同的焦点C.相同的准线D.相同的离心率解析:因为底面半径大小不等,所以长轴不同.嵌入的焦球不同,焦点不同,准线也不同,平面与圆柱的母线夹角相同,故离心率相同.答案:D3圆柱面的垂直截面是一个.答案:圆4圆柱面的一般截面是一个.答案:椭圆5如图所示,F1,F2是椭圆的两个焦点,过F1的直线交椭圆于P,Q两点,求证:△PQF2的周长为定值.证明:设椭圆的长轴长为2a.则PF1+PF2=2a,QF1+QF2=2a,所以PQ+QF2+PF2=PF1+QF1+QF2+PF2=(PF1+PF2)+(QF1+QF2)=2a+2a=4a(定值).故△PQF2的周长为定值.6如图所示,A是☉O内一定点,动圆P与☉O内切于点M,且经过点A,试判断动点P的轨迹.解:如图所示,连接PA,OM,则OM经过点P.设☉O的半径为r.∵☉O与☉P内切,∴OM=r,PA=PM,∴PO+PA=PO+PM=OM=r(常数),∴动点P的轨迹是以O,A为焦点的椭圆.1备课资源参考备选习题1.已知圆柱的底面半径为r,平面α与圆柱母线的夹角为60°,则它们交线椭圆的焦距是().A.2rB.4rC.rD.3r解析:如图,过点G2作G2H⊥AD,H为垂足,则G2H=2r.在Rt△G1G2H中,G1G2==2r×2=4r,则长轴2a=G1G2=4r,短轴2b=2r.所以焦距2c=2=2×r=2r.答案:A2.如图所示,已知A为左顶点,F是左焦点,l交OA的延长线于点B,P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是①;②;③;④;⑤.其中正确的是().A.①②B.①③④C.②③⑤D.①②③④⑤解析:①符合离心率定义;②过点Q作QC⊥l于点C,∵QC=FB,∴符合离心率定义;③∵AO=a,BO=,∴,故也是离心率;④∵AF=a-c,AB=-a,∴,∴是离心率;⑤∵FO=c,AO=a,∴是离心率.答案:D2