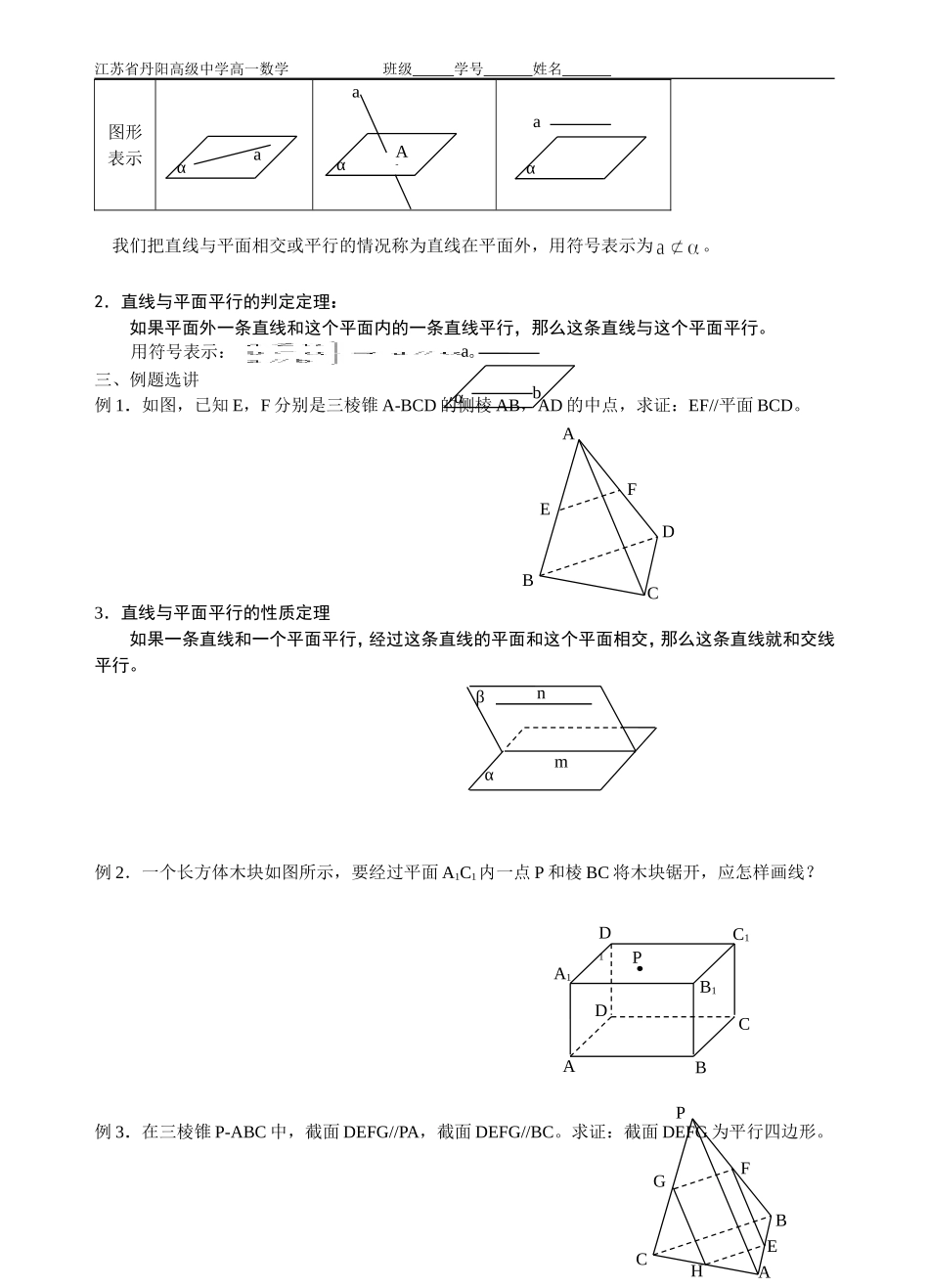
江苏省丹阳高级中学高一数学教(学)案必修②第1章立体几何初步(第9课时)第1章立体几何初步第九课时1.2.3直线与平面的位置关系(1)【教学目标】1.了解直线与平面的位置关系及图形语言和符号语言;2.了解直线与平面平行的定义;3.理解和掌握直线与平面平行的判定定理和性质定理并初步用;4.进一步培养学生的观察发现能力和空间想象能力。【教学重点】直线与平面平行的判定定理,性质定理及应用。【教学难点】直线与平面平行的性质定理的发现和理解。【过程方法】1.通过师生之间、学生之间的互相交流,促使学生的共同学习;2.通过直观感知、操作演示归纳出直线和平面的三种位置关系的概念,明确数学概念的严谨性和科学性;3.通过两个定理解决有关问题,使学生感受到化归的数学思想,培养学生科学地分析问题、解决问题的能力。【教学过程】一、引入新课观察下图正方体,回答下列问题:(1)棱(或)所在直线与平面有几个公共点;(2)对角线(或棱)所在直线与平面有几个公共点;(3)棱所在直线与平面有几个公共点。二、讲授新课1.直线与平面的位置关系如果一条直线a和一个平面α没有公共点,则称直线a与平面α平行。如果一条直线a和一个平面α有且只有一个公共点,则称直线a与平面α相交。如果一条直线a和一个平面α有无数个公共点,则称直线a在平面α内。位置关系直线a在平面α内直线a与平面α相交直线a与平面α平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示-1–ABCDA1B1D1C1江苏省丹阳高级中学高一数学班级学号姓名图形表示我们把直线与平面相交或平行的情况称为直线在平面外,用符号表示为。2.直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线与这个平面平行。用符号表示:。三、例题选讲例1.如图,已知E,F分别是三棱锥A-BCD的侧棱AB,AD的中点,求证:EF//平面BCD。3.直线与平面平行的性质定理如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。例2.一个长方体木块如图所示,要经过平面A1C1内一点P和棱BC将木块锯开,应怎样画线?例3.在三棱锥P-ABC中,截面DEFG//PA,截面DEFG//BC。求证:截面DEFG为平行四边形。αabαaαaAbαaBDCFAEβmαnABCDA1B1D1C1PAEPHFBCG江苏省丹阳高级中学高一数学教(学)案必修②第1章立体几何初步(第9课时)例4.求证:如果三个平面两两相交于三条直线,则三条交线或者相交于一点,或者互相平行。四、课堂练习1.课本P32练习1、2、3、4;2.直线a∥b,,则a与α的位置关系是()A.a∥/αB.a与α相交C.a与α不相交D.aα3.如果a,b是异面直线,且a∥平面α,那么b与α的位置关系是()A.平行B.相交C.直线在平面内D.不确定4.下面给出的四个命题,其中正确的个数是()①若,,则;②若,,则;③若∥,,则∥;④若,,则。A.0B.1C.2D.4【布置作业】1.直线在平面外,则下列说法中,正确的是(1);(2)与至少有一个公共点;(3)与至多有一个公共点;(4)与有且仅有一个公共点。2.若直线都平行于平面,则下列关于位置关系的说法中,正确的是(1)平行;(2)相交;(3)异面;(4)都有可能3下列命题中正确的是。(1)平面,则;(2)则(3)则;(4)则。4.(1)若则与有无数个公共点。(2)若,则与有一个公共点。(3)若,则与没有公共点。(4)与的关系可以分为或两类。上述命题中,正确命题是。5.如图,P为平行四边形ABCD所在平面外一点,过BC的平面与面PAD交于EF,则四边形EFBC是。-3–βαγ1a1b1c1O1βγcαba江苏省丹阳高级中学高一数学班级学号姓名6在正方体中,在上,在上,且求证:平面。7.设有平面,直线若求证。ABCDFEP