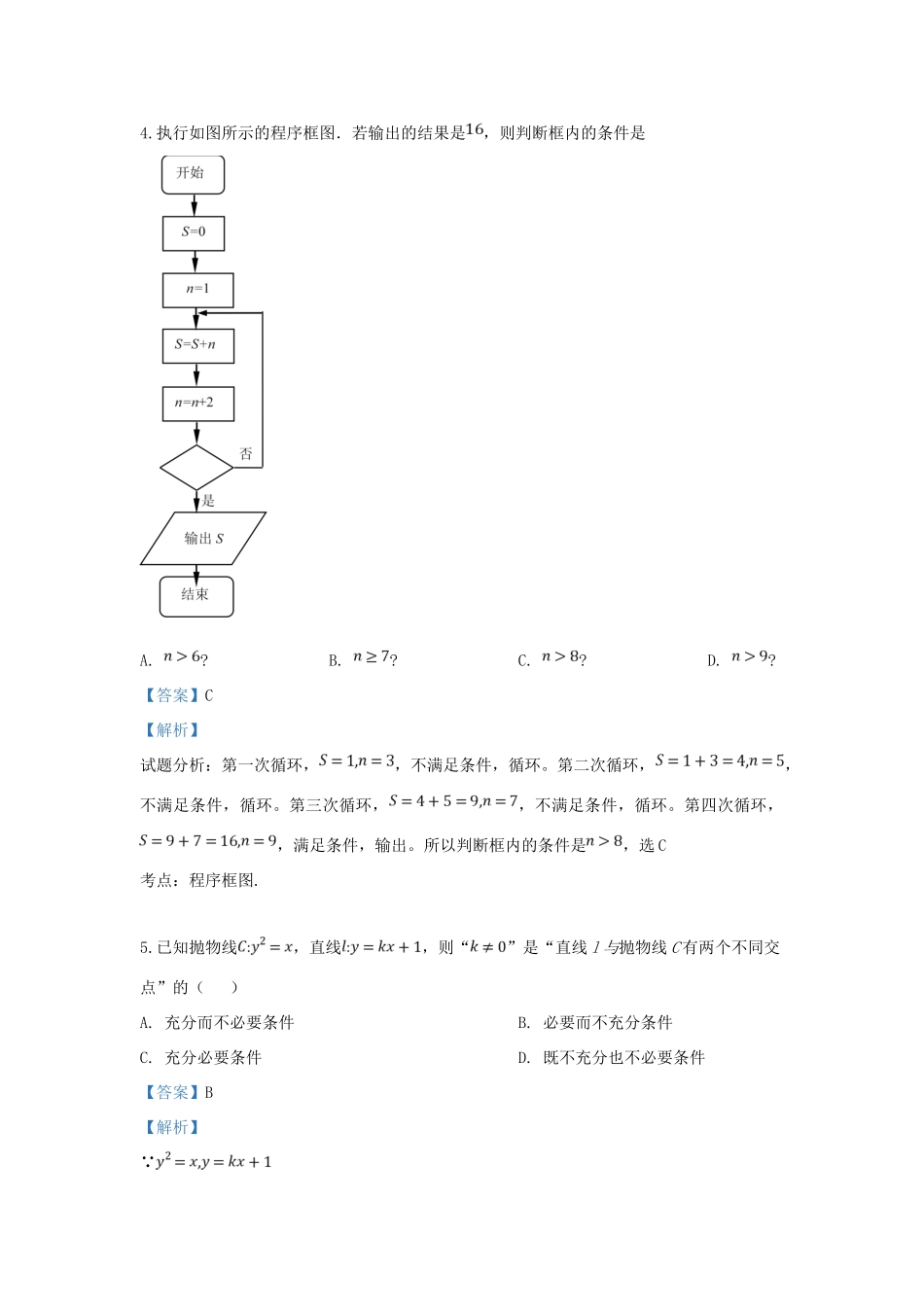
北京市大兴区2018-2019学年度第二学期高三第一次(4月)综合练习数学文科试卷一、选择题。1.已知集合,那么A∩B等于()A.B.C.D.【答案】D【解析】【分析】利用交集定义与运算,即可求解,得到答案.【详解】由题意,集合,根据集合的交集的运算,可得.故选:D.【点睛】本题主要考查了集合的表示方法,以及集合的交集的运算,其中解答中熟记集合的交集的定义域运算是解答的关键,着重考查了运算与求解能力,属于基础题.2.已知,,则()A.B.C.D.【答案】B【解析】【分析】根据指数幂的运算性质和对数运算的性质,求得的取值范围,即可求解.【详解】由题意,根据指数幂的运算性质和对数运算的性质,可得,,,∴.故选:B.【点睛】本题主要考查了指数幂的运算性质和对数的运算性质的应用,其中解答中利用指数幂的运算性质和对数的运算性质,求得的取值范围是解答的关键,着重考查了推理与运算能力,属于基础题.3.若x,y满足则的最大值为()A.B.4C.6D.8【答案】C【解析】【分析】由题得不等式组对应的可行域△ABC区域,设z=2x-y,所以y=2x-z,联立得A(4,2),再利用数形结合分析得到2x-y的最大值.【详解】由题得不等式组对应的可行域为如图所示的△ABC,设z=2x-y,所以y=2x-z,联立得A(4,2),当直线经过点A(4,2)时,直线的纵截距-z最小,z最大,此时z的最大值为=2×4-2=6.故选:C【点睛】本题主要考查利用线性规划求最值,意在考查学生对这些知识的理解掌握水平和数形结合分析推理能力.4.执行如图所示的程序框图.若输出的结果是,则判断框内的条件是A.?B.?C.?D.?【答案】C【解析】试题分析:第一次循环,,不满足条件,循环。第二次循环,,不满足条件,循环。第三次循环,,不满足条件,循环。第四次循环,,满足条件,输出。所以判断框内的条件是,选C考点:程序框图.5.已知抛物线,直线,则“”是“直线l与抛物线C有两个不同交点”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B【解析】 ∴化简可得 直线与抛物线有两个不同交点∴,且∴,且∴推导不出,且,而,且能推导出∴“”是“直线与抛物线有两个不同交点”的必要不充分条件故选B6.已知,,若,则()A.有最小值B.有最小值C.有最大值D.有最大值【答案】A【解析】【分析】根据基本不等式的性质,即可求解有最小值,得到答案.【详解】由题意,可知,,且,因为,则,即,所以,当且仅当时,等号成立,取得最小值,故选:A.【点睛】本题主要考查了基本不等式的应用,其中解答中合理应用基本不等式求解是解答的关键,着重考查了运算与求解能力,属于基础题.7.某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为()A.B.3C.D.【答案】C【解析】【分析】根据三视图,还原出原图,根据几何体的结构特征,利用勾股定理,即可求解,得到答案.【详解】根据题意,该三棱锥的原图为如图的S-ABC,其中SD在俯视图中投成了一个点,故SD⊥平面ABCD(ABCD为俯视图的四个顶点),DE平行于正视的视线,故DE⊥BC,根据题意,知DE=BE=SD=2,所以SB为最长的棱,因为BD⊂ABCD,∴SD⊥BD,∴,则.故选:C.【点睛】本题考查了空间几何体的三视图的应用,以及空间几何体的结构特征,其中解答中由三视图还原原图是解决问题的难点,着重考查了分析问题和解答问题的能力,属于中档题.8.有10名选手参加某项诗词比赛,计分规则如下:比赛共有6道题,对于每一道题,10名选手都必须作答,若恰有n个人答错,则答对的选手该题每人得n分,答错选手该题不得分.比赛结束后,关于选手得分情况有如下结论:①若选手甲答对6道题,选手乙答对5道题,则甲比乙至少多得1分;②若选手甲和选手乙都答对5道题,则甲和乙得分相同;③若选手甲的总分比其他选手都高,则甲最高可得54分④10名选手的总分不超过150分.其中正确结论的个数是()A.4B.3C.2D.1【答案】B【解析】【分析】根据题意,利用题设所给的规则逐项进行判断,即可求解,得到答案.【详解】由题意,①甲全对,得到全部题目分数,乙错一道题,比甲少1题的分数,且这一题至少为1分(至少1人答错),故甲比乙至少多得1分;②若选手甲和选手乙都答对5道题,如...