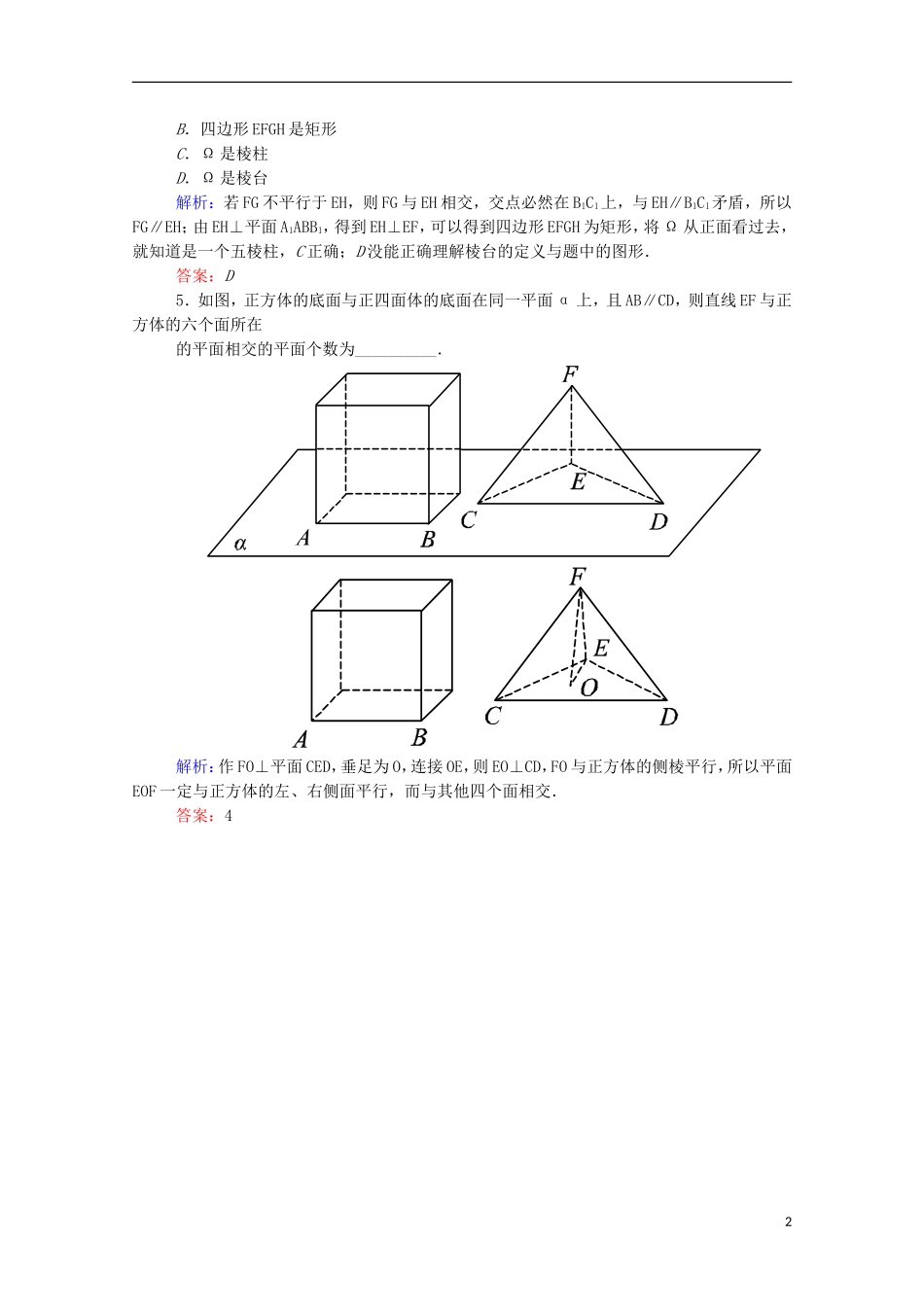
【状元之路】2016届高考数学理一轮总复习第7章立体几何练习3(含解析)新人教A版1.在下列命题中,不是公理的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线解析:由立体几何基本知识知,B项为公理2,C项为公理1,D项为公理3,A项不是公理.答案:A2.下列命题中,真命题的个数为()①两条直线可以确定一个平面②若M∈α,M∈β,α∩β=l,则M∈l③空间中,相交于同一点的三条直线在同一平面内A.1个B.2个C.3个D.0个解析:两异面直线不能确定一个平面,故①不正确;在空间交于一点的三条直线不一定共面(如墙角),故③不正确;据平面的性质可知②正确.答案:A3.以下四个命题中,正确命题的个数是()①不共面的四点中,其中任意三点不共线②若点A、B、C、D共面,点A、B、C、E共面,则A、B、C、D、E共面③若直线a、b共面,直线a、c共面,则直线b、c共面④依次首尾相接的四条线段必共面A.0个B.1个C.2个D.3个解析:①假设其中有三点共线,则该直线和直线外的另一点确定一个平面.这与四点不共面矛盾,故其中任意三点不共线,所以①正确.②从条件看出两平面有三个公共点A、B、C,但是若A、B、C共线,则结论不正确;③不正确;④不正确,因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形.答案:B4.如图,若Ω是长方体ABCDA1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是()A.EH∥FG1B.四边形EFGH是矩形C.Ω是棱柱D.Ω是棱台解析:若FG不平行于EH,则FG与EH相交,交点必然在B1C1上,与EH∥B1C1矛盾,所以FG∥EH;由EH⊥平面A1ABB1,得到EH⊥EF,可以得到四边形EFGH为矩形,将Ω从正面看过去,就知道是一个五棱柱,C正确;D没能正确理解棱台的定义与题中的图形.答案:D5.如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,则直线EF与正方体的六个面所在的平面相交的平面个数为__________.解析:作FO⊥平面CED,垂足为O,连接OE,则EO⊥CD,FO与正方体的侧棱平行,所以平面EOF一定与正方体的左、右侧面平行,而与其他四个面相交.答案:42