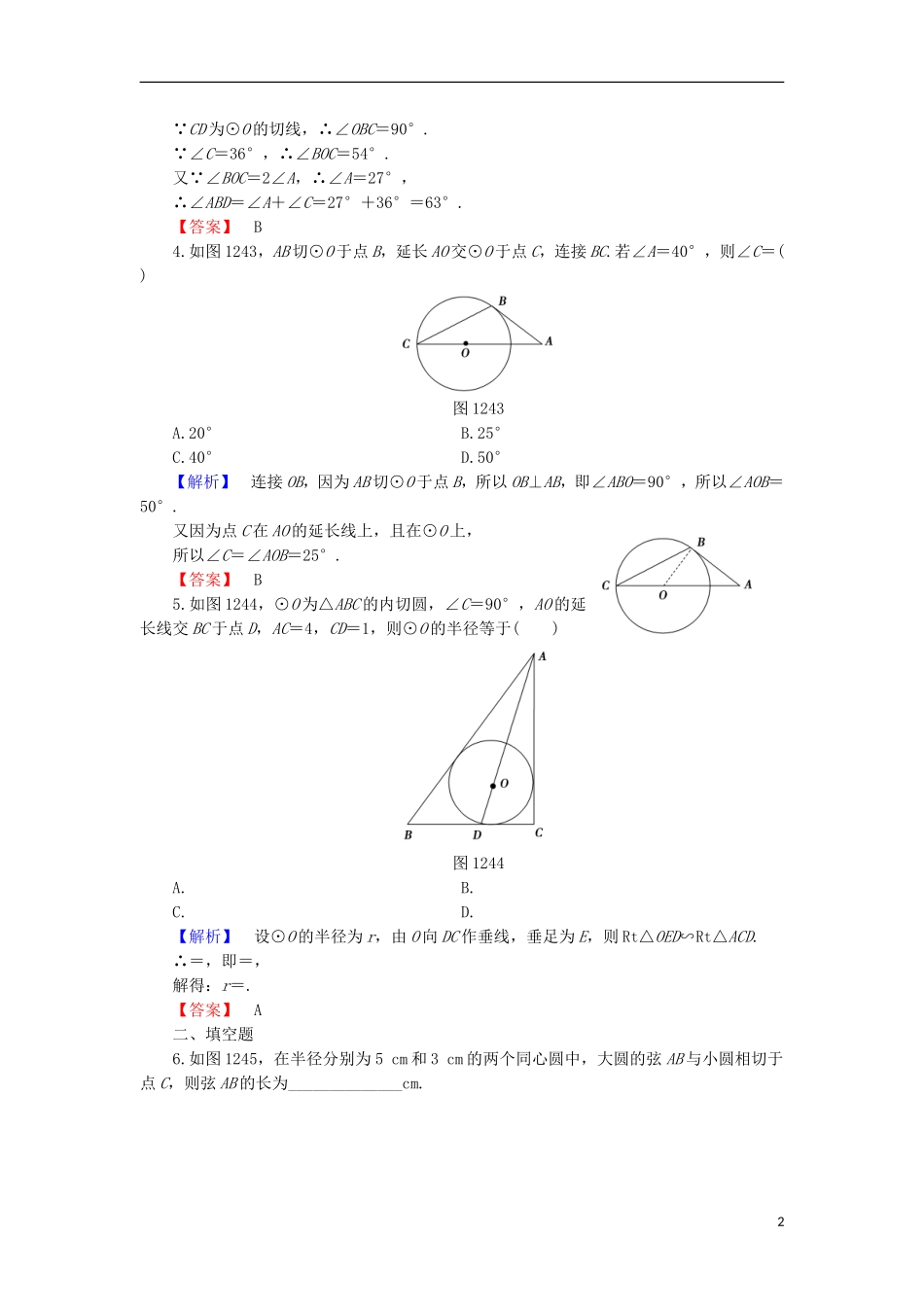
学业分层测评(五)2.2圆的切线的判定和性质(建议用时:45分钟)学业达标]一、选择题1.下列说法:①与圆有公共点的直线是圆的切线;②垂直于圆的半径的直线是圆的切线;③与圆心的距离等于半径的直线是圆的切线;④过直径的端点,垂直于此直径的直线是圆的切线,其中正确的是()A.①②B.②③C.③④D.①④【解析】由圆的切线的定义知①②不正确,③④正确.【答案】C2.如图1241,⊙O的半径为2,点O到直线l的距离为3,点P为直线l上的一个动点,PB切⊙O于点B,则PB的最小值是()图1241A.B.C.D.【解析】 PB切⊙O于点B,∴∠OBP=90°,∴PB2=OP2-OB2,而OB=2,∴PB2=OP2-4,即PB=,当OP最小时,PB最小, 点O到直线l的距离为3,∴OP的最小值为3,∴PB的最小值为=.【答案】A3.如图1242,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是()图1242A.72°B.63°C.54°D.36°【解析】连接OB.1 CD为⊙O的切线,∴∠OBC=90°. ∠C=36°,∴∠BOC=54°.又 ∠BOC=2∠A,∴∠A=27°,∴∠ABD=∠A+∠C=27°+36°=63°.【答案】B4.如图1243,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=()图1243A.20°B.25°C.40°D.50°【解析】连接OB,因为AB切⊙O于点B,所以OB⊥AB,即∠ABO=90°,所以∠AOB=50°.又因为点C在AO的延长线上,且在⊙O上,所以∠C=∠AOB=25°.【答案】B5.如图1244,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于()图1244A.B.C.D.【解析】设⊙O的半径为r,由O向DC作垂线,垂足为E,则Rt△OED∽Rt△ACD.∴=,即=,解得:r=.【答案】A二、填空题6.如图1245,在半径分别为5cm和3cm的两个同心圆中,大圆的弦AB与小圆相切于点C,则弦AB的长为______________cm.2图1245【解析】连接OA,OC, AB是小圆的切线,∴OC⊥AB,∴AC=AB. 在Rt△AOC中,AC==4(cm),∴AB=8cm.【答案】87.如图1246所示,AC切⊙O于D,AO的延长线交⊙O于B,且AB⊥BC,若AD∶AC=1∶2,则AO∶OB=______.【导学号:96990022】图1246【解析】如图所示,连接OD,则OD⊥AC. AC是⊙O的切线,∴OB=OD,OC=OC,∠ODC=∠OBC=90°.∴△CDO≌△CBO.∴BC=DC. =,∴AD=DC.∴BC=AC.又OB⊥BC,∠ABC=90°,∴∠A=30°.∴OB=OD=AO.∴=.【答案】2∶18.圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于点D,E,则∠DAC=__________,DC=__________.【解析】连接OC, OC=OB,∴∠OCB=∠OBC.又∠DCA+∠ACO=90°,∠ACO+∠OCB=90°,∴∠DCA=∠OCB, OC=3,BC=3,∴△OCB是正三角形.∴∠OBC=60°,即∠DCA=60°.∴∠DAC=30°.在Rt△ACB中,AC==3,3DC=ACsin30°=.【答案】30°三、解答题9.如图1247,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,且∠AOD=∠APC.求证:AP是⊙O的切线.图1247【证明】连接OP. PD⊥BE,∴∠OCD=90°.∴∠ODC+∠COD=90°. OD=OP,∴∠ODC=∠OPC. ∠AOD=∠APC,∴∠OPC+∠APC=90°.∴∠APO=90°,即AP⊥PO.∴AP是⊙O的切线.10.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm.(1)求△ABC内切圆的半径;(2)若移动圆心O的位置,使⊙O保持与△ABC的边AC和边BC都相切,求r的取值范围.【解】(1)如图所示,⊙O是Rt△ABC的内切圆,切点分别为D,E,F.连接OD,OE,OF,OB,则OD⊥BC,OE⊥AC,OF⊥AB.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,∴AB=5cm. OE=OD,∠C=90°,∴四边形CEOD是正方形.∴CD=DO. OB=OB,OD=OF,∠ODB=∠OFB=90°,∴△ODB≌△OFB.∴BD=BF.同理可得,AE=AF.∴AC+BC-AB=AE+EC+BD+DC-AF-BF=EC+DC=2OD.∴内切圆的半径r=OD===1cm.(2)如图所示,动⊙O与AC,BC相切的最大的圆与AC,BC的切点分别是A,D,连接OA,OD,则四边形AODC是正方形,此时应有OA=AC=3cm,∴动圆的半径r的范围为(0,3].能力提升]41.AB是⊙O的切线,在下列给出的条件中,能判定AB⊥CD的是()A.AB与⊙O相切于直线CD上的点CB.CD经过圆心OC.CD是直径D.AB与⊙O相切于C,CD过圆心O【解析】圆...