高中数学 一元二次不等式的解法练习 新人教版必修5-新人教版高二必修5数学试题VIP免费

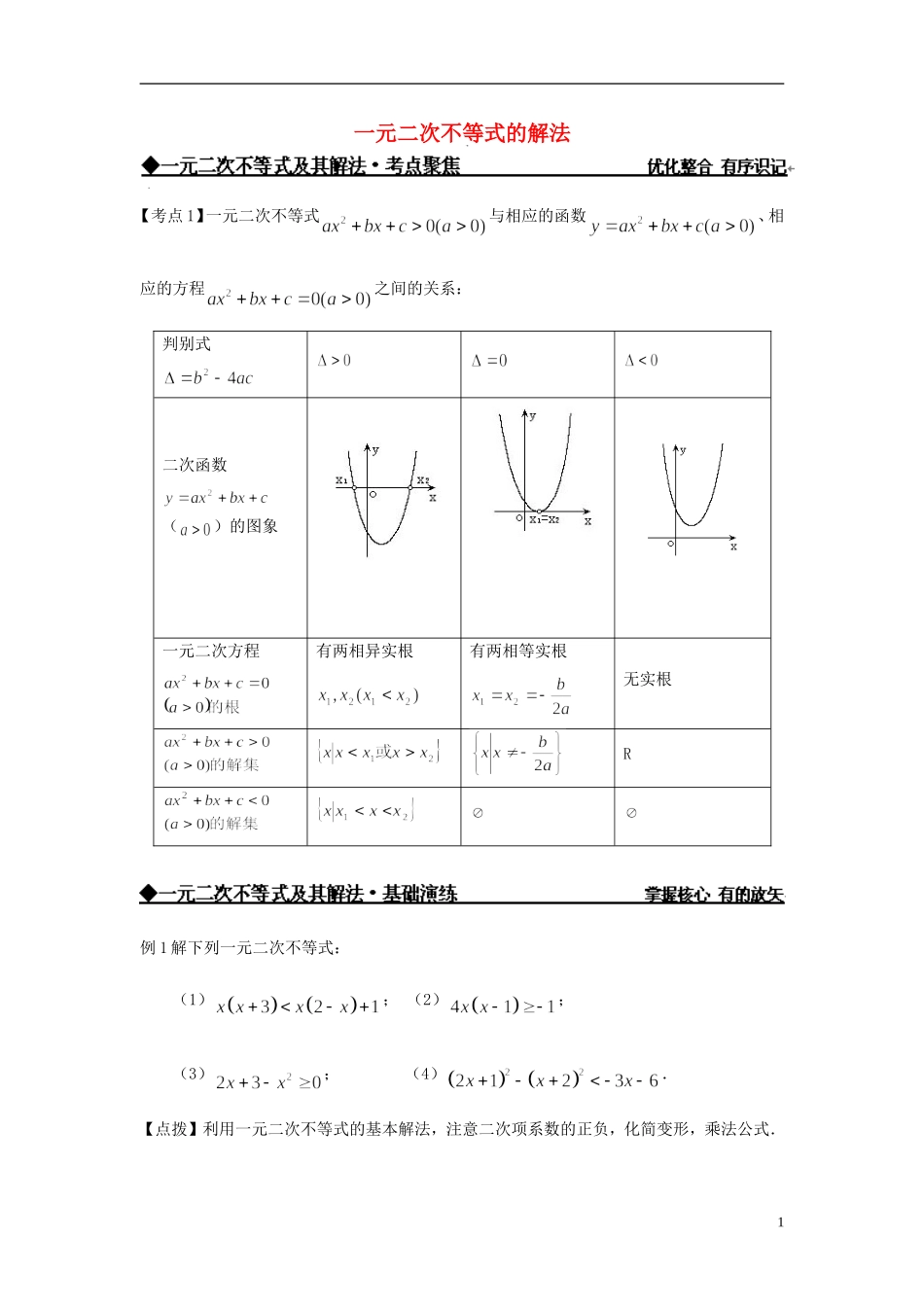
一元二次不等式的解法【考点1】一元二次不等式与相应的函数、相应的方程之间的关系：判别式二次函数（）的图象一元二次方程有两相异实根有两相等实根无实根R例1解下列一元二次不等式：（1）；（2）；（3）；（4）．【点拨】利用一元二次不等式的基本解法，注意二次项系数的正负，化简变形，乘法公式．1【解析】（1）整理得，解集为．（2）整理得，解集为R．（3）整理得，解集为．（4）整理得，解集为．【小结】本题考查一元二次不等式的基本解法．变式1：不等式≤2的解集是．【解析】原不等式可化为≤0，即≤0，即（x+3）（x+8）≥0且,解得：≤-8或．变式2：不等式1)3)(2)(1(xxxx≤0的解集是．【解析】穿根法．【答案】．练习1：不等式0322322xxxx的解集为．【解题过程】【解析】 0322322xxxx0320)32)(23(222xxxxxx20)1)(3(0)1)(3)(2)(1(xxxxxx，∴原不等式的解集为{x|-10的解集；（2）若不等式f（x）＋1>0的解集为（，3），求m的值．【解析】（1）当m＝1时，f（x）>0，即2x2－x>0⇒x（2x－1）>0⇒x<0，或x>．∴此时不等式的解集为（－∞，0）∪（，＋∞）．（2）由f（x）＋1>0，得（m＋1）x2－mx＋m>0． 不等式的解集为（，3），∴和3是方程（m＋1）x2－mx＋m＝0的两个根，且m＋1<0．∴解得m＝－．【答案】（1）（－∞，0）∪（，＋∞）；（2）m＝－．练习2：若不等式的解是2＜x＜3，求不等式的解集．【解题过程】【考点2】解含参数不等式解任意含参数（单参）的一元二次不等式对参数进行分类讨论时只需求出二次项系数等于零和判别式时所得到的参数的值，然后依此进行分类即可．例3解关于的不等式：．【点拨】求判别式时所得到的参数的值，然后依此进行分类．【解析】，3此时两根为，．（1）当时，，解集为（）（）；（2）当时，，解集为（）（）；（3）当时，，解集为；（4）当时，，解集为（）（）；（5）当时，，解集为（）（）．练习3：解关于x的不等式：ax2-（a+1）x+1<0．【解题过程】【解析】（1）当a=0时，原不等式可化为-x+1<0，即x>1；（2）当a≠0时，原不等式可化为a（x-1）<0，①若a<0，则原不等式可化为（x-1）>0，由于<0，则有<1，故解得4x<或x>1；②若a>0，则原不等式可化为（x-1）<0，则有ⅰ．当a>1时，则有<1，故解得1，故解得11}；当a=0时，解集为{x|x>1}；当01时，解集为{x|