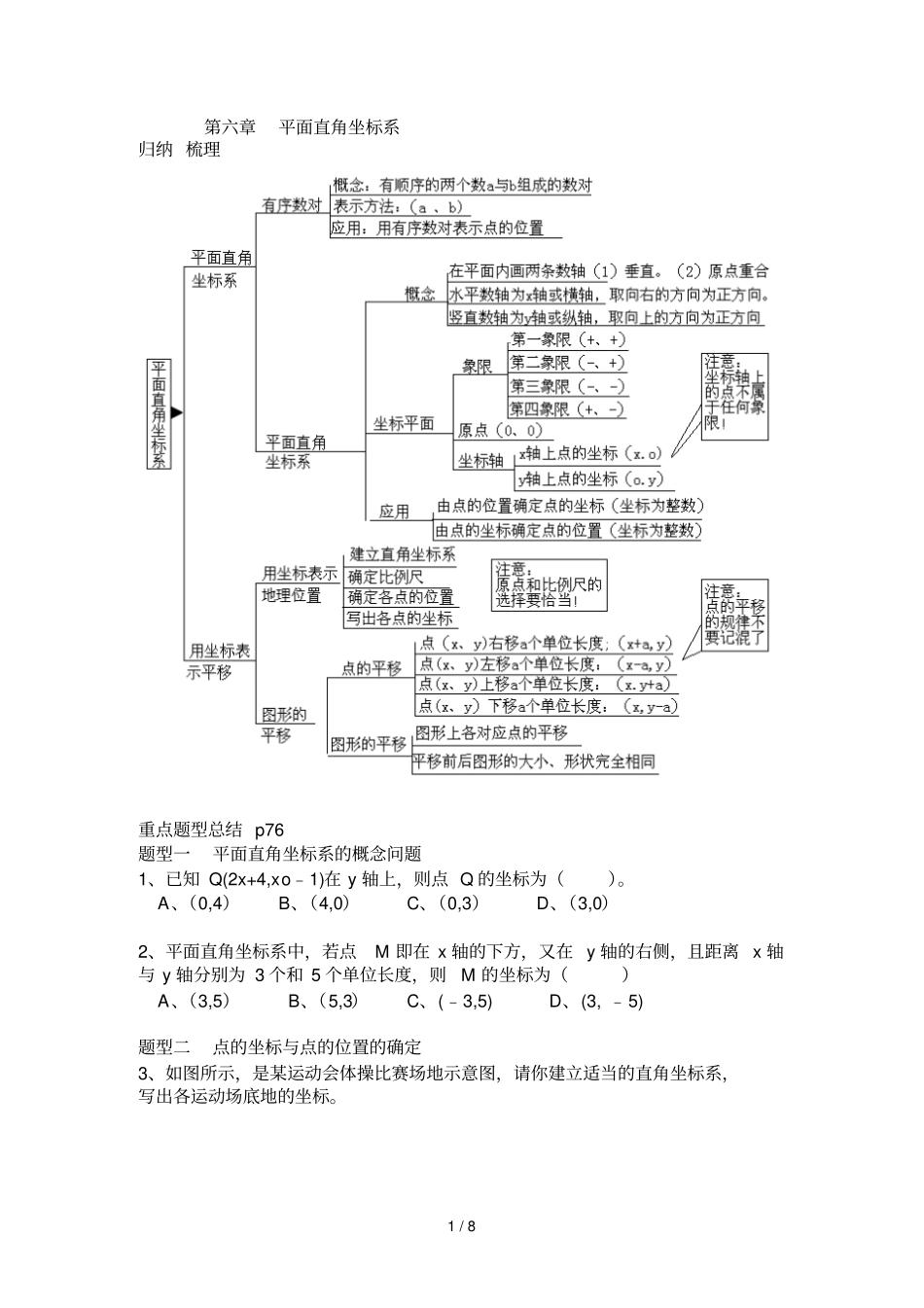
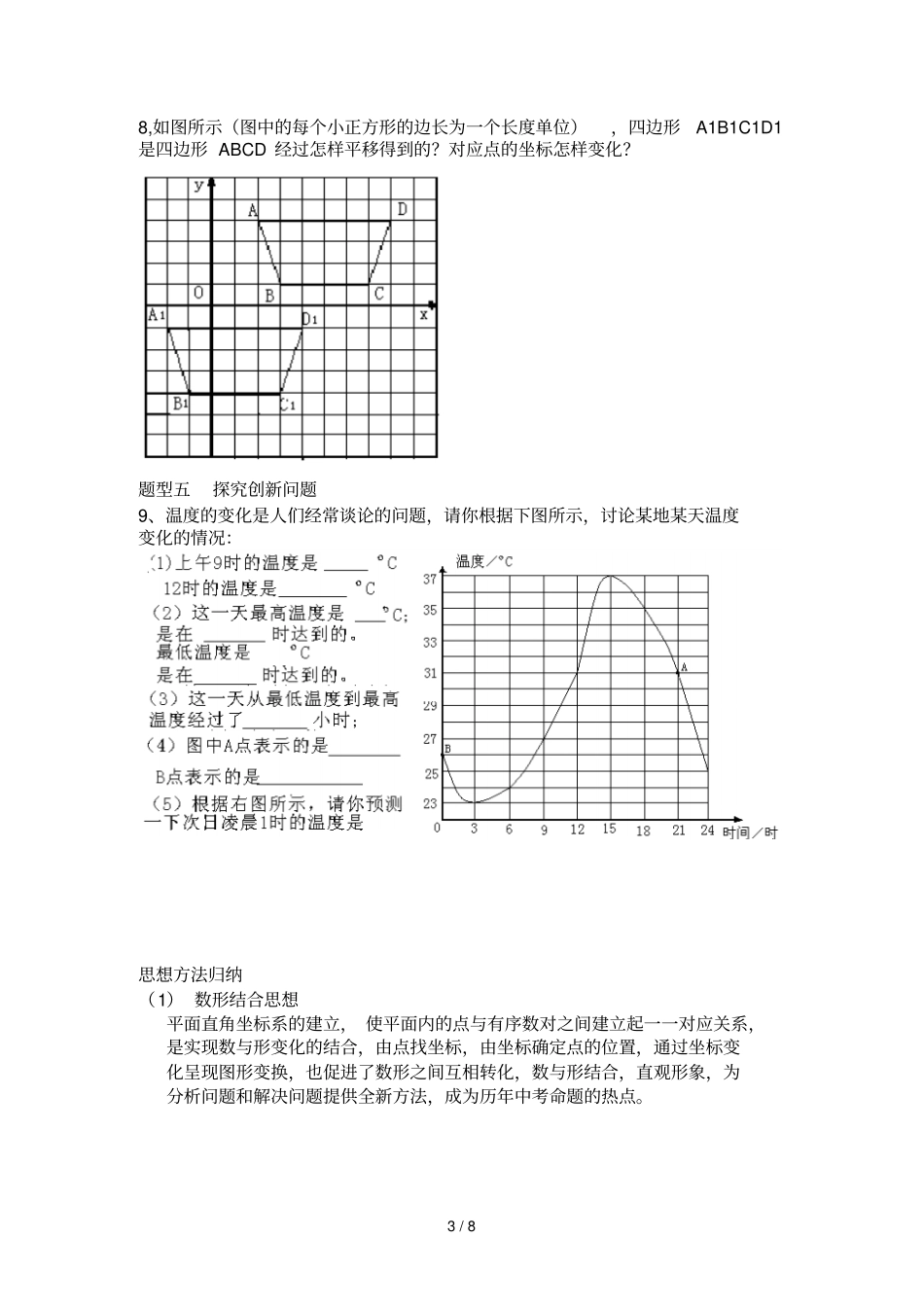
1/8第六章平面直角坐标系归纳梳理重点题型总结p76题型一平面直角坐标系的概念问题1、已知Q(2x+4,xo﹣1)在y轴上,则点Q的坐标为()。A、(0,4)B、(4,0)C、(0,3)D、(3,0)2、平面直角坐标系中,若点M即在x轴的下方,又在y轴的右侧,且距离x轴与y轴分别为3个和5个单位长度,则M的坐标为()A、(3,5)B、(5,3)C、(﹣3,5)D、(3,﹣5)题型二点的坐标与点的位置的确定3、如图所示,是某运动会体操比赛场地示意图,请你建立适当的直角坐标系,写出各运动场底地的坐标。2/84、某地区立体两条交通干线L1与L2互相垂直,并交于O,L1为南北方向,L2为东西方向。现以L2为x轴,L1为y轴,取100km为1个单位长度建立直角坐标系,根据地震监测部门预报,该地区最近将有一次地震,震中位置在P(1,﹣2),影响范围半径为300km.(1)根据题意画出直角坐标系,并标出震中位置。(2)在平面直角坐标系内画出地震影响范围,并判断下列城市是否受到地震影响。城市:O(0,0),A(﹣3,0)B(0,1)C(﹣1.5,﹣4)D(0,﹣4)E(2,﹣4)题型三平面直角坐标系在实际问题中的应用(P79)5、已知点A(0,0),B(3,0),点C在y轴上,且三角形ABC的面积是5,求点C的坐标。6、如图所示的【,平面直角坐标系中,四边形ABCD各定点的坐标分别为A(0,0)B(9,0)C,(7,5)D,(2,7),试确定四边形的面积。题型四图形的平移变换及点的坐标变化(P80)7、三角形A1B1C1是经过三角形ABC平移得到的,三角形ABC中的任意一点P(x0,y0)经过平移后得到的对应点P1的坐标为(x0+3,y0+1),已知三角形ABC三个顶点的坐标分别是A(﹣1,1),B(﹣2,﹣2),C(0,0)则三角形A1B1C1各顶点的坐标分别为。3/88,如图所示(图中的每个小正方形的边长为一个长度单位),四边形A1B1C1D1是四边形ABCD经过怎样平移得到的?对应点的坐标怎样变化?题型五探究创新问题9、温度的变化是人们经常谈论的问题,请你根据下图所示,讨论某地某天温度变化的情况:思想方法归纳(1)数形结合思想平面直角坐标系的建立,使平面内的点与有序数对之间建立起一一对应关系,是实现数与形变化的结合,由点找坐标,由坐标确定点的位置,通过坐标变化呈现图形变换,也促进了数形之间互相转化,数与形结合,直观形象,为分析问题和解决问题提供全新方法,成为历年中考命题的热点。4/8A.将△ABC先向下平移1个单位长度,在向左平移4个单位长度.B.将△ABC先向上平移1个单位长度,在向左平移4个单位长度。C.将△ABC先向右平移4个单位长度,在向上平移1个单位长度。D.将△ABC先向左平移4个单位长度,在向下平移1个单位长度。(2)分类讨论思想在平面直角坐标系中,所研究的问题有时也包括多种情况,因而,必须按可能出现的所有情况来分别讨论,得出各种情况下相应的结论,从而使得复杂问题得以解决。2、长方形ABCD的边长AB=4,BC=6,若将该长方形放在平面直角坐标系中,使点A在坐标为(-1,2)且AB∥x轴,试求点C的坐标。(2)转化思想在解决平面直角坐标系中的问题时,要学会把较生僻、繁琐的问题化归为较为简单熟悉的问题,从而使问题轻而易举地得以解决。3、如图所示,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积。中考考点对接(61)1、(2010.成都)在平面直角坐标系中,点A(1,-3)位于第象限.5/82、(P62)2010(山东潍坊中考)如图6-1-3所示,雷达探测得六个目标A、B、C、D、E、F出现,按照规定的目标表示C、F的位置表示为C(6,120o)、F(5,210o)按照此方法在表示目标A、B、D、E的位置时,其中表示不正确的是().A、A(5,30o)B、B(2,90oC、D(4,240o)D、E(3,60o)中考考点对接中考典题剖析(P72)3、(P72)(2010.珠海中考)在平面直角坐标系中,将点P(﹣2,3)沿x轴方向向右平移3个单位长度得到点Q,则点Q点坐标是().A、(-2,6)B、(-2,0)C、(-5,3)D、(1,3)4、教材54页习题6.2第4题如图6-2-12所示,将三角形向右平移2个单位长度,再向上平移3单位长度,则平移后三个顶点的坐标是()A、(2,2),(3,4),(1,7)B、(-2,2),(4,3),(1,7)C、(-2,2),(3,4),(1,7)D、(2,-2),(3,3),(1,7)5、(2010.山东聊城中考)已知△ABC在平面直...