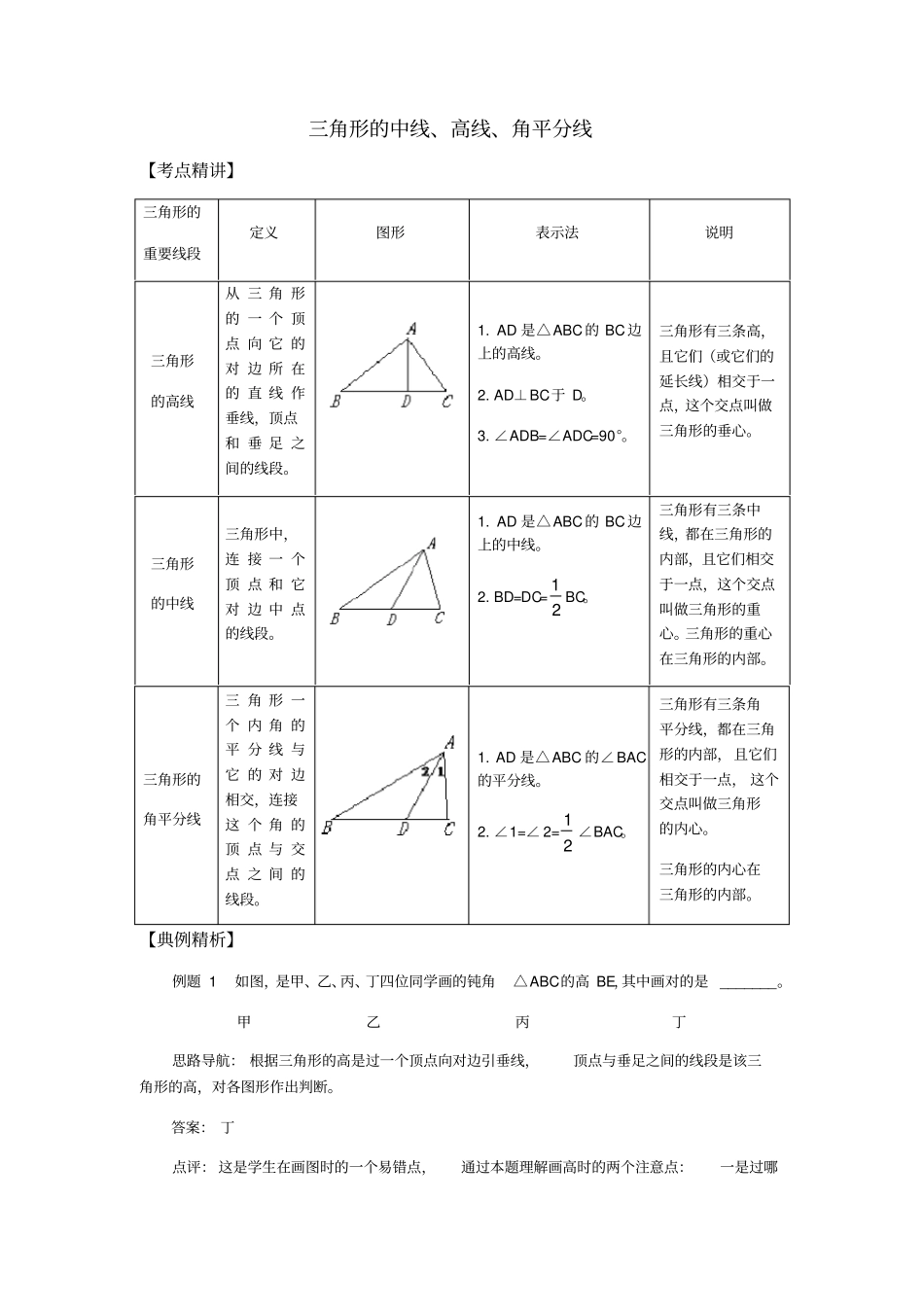
三角形的中线、高线、角平分线【考点精讲】三角形的重要线段定义图形表示法说明三角形的高线从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段。1.AD是△ABC的BC边上的高线。2.AD⊥BC于D。3.∠ADB=∠ADC=90°。三角形有三条高,且它们(或它们的延长线)相交于一点,这个交点叫做三角形的垂心。三角形的中线三角形中,连接一个顶点和它对边中点的线段。1.AD是△ABC的BC边上的中线。2.BD=DC=12BC。三角形有三条中线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形的重心。三角形的重心在三角形的内部。三角形的角平分线三角形一个内角的平分线与它的对边相交,连接这个角的顶点与交点之间的线段。1.AD是△ABC的∠BAC的平分线。2.∠1=∠2=12∠BAC。三角形有三条角平分线,都在三角形的内部,且它们相交于一点,这个交点叫做三角形的内心。三角形的内心在三角形的内部。【典例精析】例题1如图,是甲、乙、丙、丁四位同学画的钝角△ABC的高BE,其中画对的是_______。甲乙丙丁思路导航:根据三角形的高是过一个顶点向对边引垂线,顶点与垂足之间的线段是该三角形的高,对各图形作出判断。答案:丁点评:这是学生在画图时的一个易错点,通过本题理解画高时的两个注意点:一是过哪个点;二是垂直于哪条边。这道题是过B点,垂直于AC边。例题2等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,则这个等腰三角形的底边长是______。思路导航:根据等腰三角形的性质和已知条件求出腰长和底边长,然后根据三边关系进行讨论,即可得出结论。答案:设等腰三角形的腰长是xcm,底边是ycm。根据题意,得:212122xyxx或122212xyxx,解得:178yx或514yx根据三角形的三边关系,知:8,8,17不能组成三角形,应舍去。所以它的底边是5cm。点评:本题考查了等腰三角形的性质;解题中,因为两部分的周长没有明确,所以首先要分两种情况考虑。最后一定要注意检查结果是否符合三角形的三边关系。分类讨论是解题的关键。例题3如图,D为△ABC中BC边上的任意一点(不与B、C重合),AE和AF分别是△ABD和△ACD的角平分线。求证:∠EAF=21∠BAC。思路导航:从三角形的角平分线的定义,你能得到什么呢AE是△ABD的角平分线,得到∠3=∠4=21∠BAD;AF是△ACD的角平分线,得到∠1=∠2=21∠CAD。从需要求证的∠EAF我们想到它等于∠3+∠2,再通过计算,就可以得到结论。答案: AE和AF分别是△ABD和△ACD的角平分线,∴∠3=∠4=21∠BAD,∠1=∠2=21∠CAD,∴∠3+∠2=21∠BAD+21∠CAD=21(∠BAD+∠CAD)=21∠CAB,即∠EAF=21∠BAC。点评:三角形的角平分线和角的平分线的用法是一样的,但是它们的概念本质不一样,三角形的角平分线是一条线段,而角的平分线是一条射线。例题4有一块三角形绿地,现在要把它分成面积相等的四块三角形,请你设计一个可行的方案,并画出示意图。思路导航:根据“等(同)底等(同)高的三角形面积相等”,结合三角形的中线、等分点的定义去设计方案。答案:如图①所示:先找出AC的中点D,再连接DB,再找出DB的中点E,连接AE、CE,就可以把三角形的绿地分成面积相等的四块;如图②所示:先找出AB的中点D,再连接DC,再找出DC的中点E,连接AE,找到BC的中点F,连接DF,就可以把三角形的绿地分成面积相等的四块。图①图②点评:本题属于方案设计类问题。实质是把一个三角形分成面积相等的四个三角形,“等(同)底等(同)高的三角形面积相等”是根本依据,还有很多方案,只要满足条件均可。如下图所示:【总结提升】三角形的高、中线和角平分线是三角形的三种重要线段,它们都分别交于一点,且三角形的三条中线和三条角平分线都分别交于三角形的内部;而锐角三角形三条高线都在三角形的内部且相交于一点;直角三角形有两条高分别与两直角边重合,另一条高在三角形内部,它们交于直角顶点;钝角三角形有两条高在三角形的外部,一条高在三角形的内部,三条高所在直线交于三角形外一点。同步测试三角形的中线、高线、角平分线一、选择题*1.等腰三角形的底边长为5cm,一腰上的中线把原三角形的周长分成两部分,其差为3cm,则腰长为()A.2cmB.8cmC.2cm或...