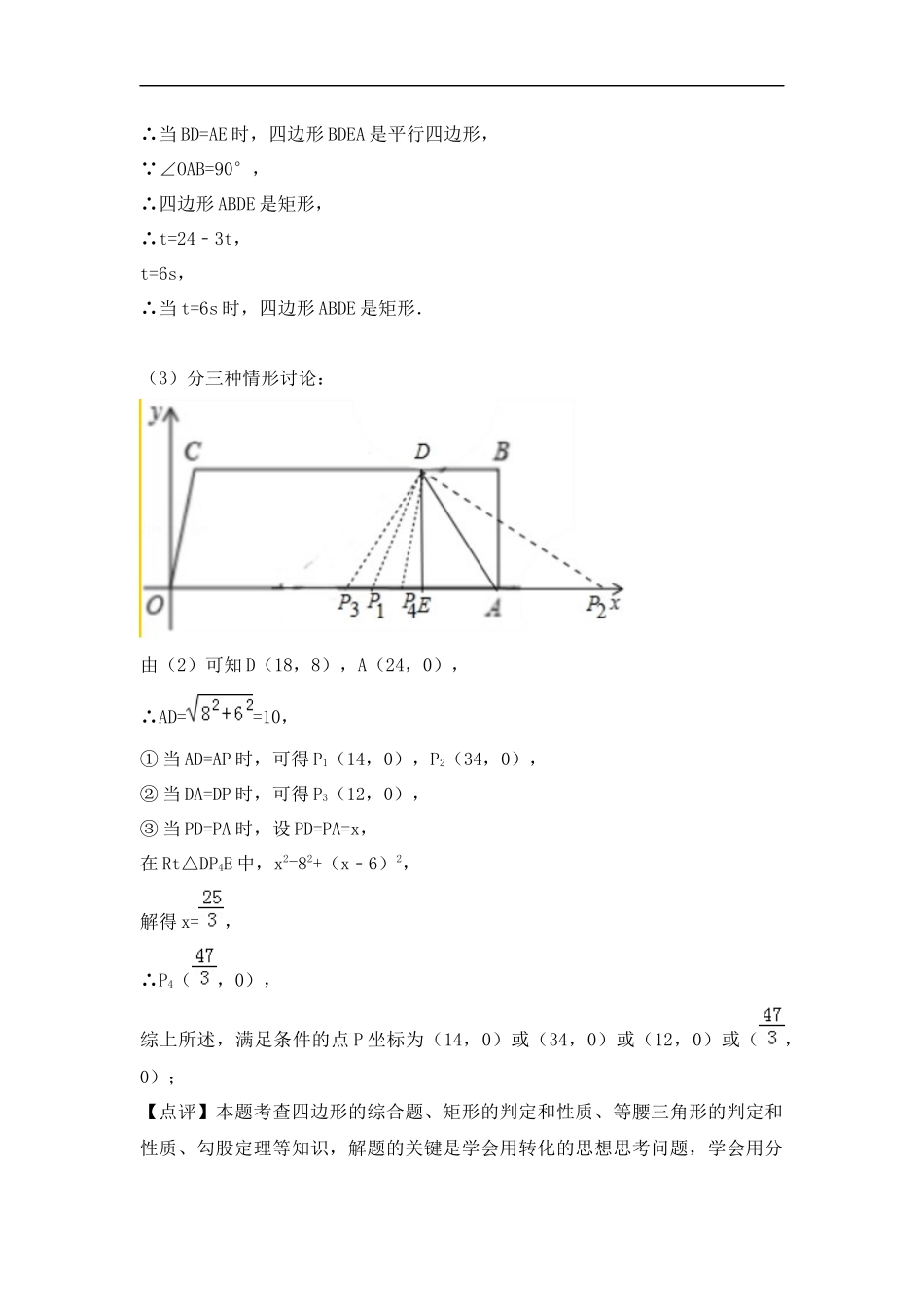
八年级下数学期末压轴题精选1.等腰三角形存在性(2017广西柳州)23.(10分)如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点B的坐标为(24,8),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿OA向A运动,当点E达到点A时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.(1)连接AD,记△ADE得面积为S,求S与t的函数关系式,写出t的取值范围;(2)当t为何值时,四边形ABDE是矩形;(3)在(2)的条件下,当四边形ABDE是矩形,在x轴上找一点P,使得△ADP为等腰三角形,直接写出所有满足要求的P点的坐标.【分析】(1)根据三角形面积公式计算即可;(2)当BD=AE时,四边形ABDE是矩形,由此构建方程即可解决问题;(3)分三种情形:①当AD=AP时,②当DA=DP时,③当PD=PA时,分别求解即可;【解答】解:(1)如图1中,S=×(24﹣3t)×8=﹣12t+96(0≤t≤8).(2) OA∥BD,∴当BD=AE时,四边形BDEA是平行四边形, ∠OAB=90°,∴四边形ABDE是矩形,∴t=24﹣3t,t=6s,∴当t=6s时,四边形ABDE是矩形.(3)分三种情形讨论:由(2)可知D(18,8),A(24,0),∴AD==10,①当AD=AP时,可得P1(14,0),P2(34,0),②当DA=DP时,可得P3(12,0),③当PD=PA时,设PD=PA=x,在Rt△DP4E中,x2=82+(x﹣6)2,解得x=,∴P4(,0),综上所述,满足条件的点P坐标为(14,0)或(34,0)或(12,0)或(,0);【点评】本题考查四边形的综合题、矩形的判定和性质、等腰三角形的判定和性质、勾股定理等知识,解题的关键是学会用转化的思想思考问题,学会用分类讨论的思想解决问题,属于中考压轴题.2.直角三角形存在性(2017深圳新华)如图,在平面直角坐标系中,O是坐标原点,平行四边形的顶点C的坐标为(8,8),顶点A的坐标为(﹣6,0),边AB在x轴上,点E为线段AD的中点,点F在线段DC上,且横坐标为3,直线EF与y轴交于点G,有一动点P以每秒1个单位长度的速度,从点A沿折线A﹣B﹣C﹣F运动,当点P到达点F时停止运动,设点P运动时间为t秒.(1)求直线EF的表达式及点G的坐标;(2)点P在运动的过程中,设△EFP的面积为S(P不与F重合),试求S与t的函数关系式;(3)在运动的过程中,是否存在点P,使得△PGF为直角三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【分析】(1)根据点C的坐标可求出点F的纵坐标,结合题意可得出点F的坐标,过点E作EH⊥x轴于点H,利用△AHE∽△AOD,可求出点E的坐标,从而利用待定系数法可确定直线EF的解析式,令x=0,可得出点G的坐标.(2)延长HE交CD的延长线于点M,讨论点P的位置,①当点P在AB上运动时,②当点P在BC边上运动时,③当点P在CF上运动时,分别利用面积相减法可求出答案.(3)很明显在BC上存在两个点使△PGF为直角三角形,这两点是通过①过点G作GP⊥EF,②过点F作FP⊥EF得出来的.【解答】解:(1) C(8,8),DC∥x轴,点F的横坐标为3,∴OD=CD=8.∴点F的坐标为(3,8), A(﹣6,0),∴OA=6,∴AD=10,过点E作EH⊥x轴于点H,则△AHE∽△AOD.又 E为AD的中点,∴===.∴AH=3,EH=4.∴OH=3.∴点E的坐标为(﹣3,4),设过E、F的直线为y=kx+b,∴∴∴直线EF为y=x+6,令x=0,则y=6,即点G的坐标为(0,6).(2)延长HE交CD的延长线于点M,则EM=EH=4. DF=3,∴S△DEF=×3×4=6,且S平行四边形ABCD=CD•OD=8×8=64.①当点P在AB上运动时,如图3,S=S平行四边形ABCD﹣S△DEF﹣S△APE﹣S四边形PBCF. AP=t,EH=4,∴S△APE=×4t=2t,S四边形PBCF=(5+8﹣t)×8=52﹣4t.∴S=64﹣6﹣2t﹣(52﹣4t),即:S=2t+6.②当点P在BC边上运动时,S=S平行四边形ABCD﹣S△DEF﹣S△PCF﹣S四边形ABPE.过点P作PN⊥CD于点N. ∠C=∠A,sin∠A==,∴sin∠C=. PC=18﹣t,∴PN=PC•sin∠C=(18﹣t). CF=5,∴S△PCF=×5×(18﹣t)=36﹣2t.过点B作BK⊥AD于点K. AB=CD=8,∴BK=AB•sin∠A=8×=. PB=t﹣8,∴S四边形ABPE=(t﹣8+5)×=t﹣.∴S=64﹣6﹣(36﹣2t)﹣(t﹣),即S=﹣t+.(8分)③当点P在CF上运...