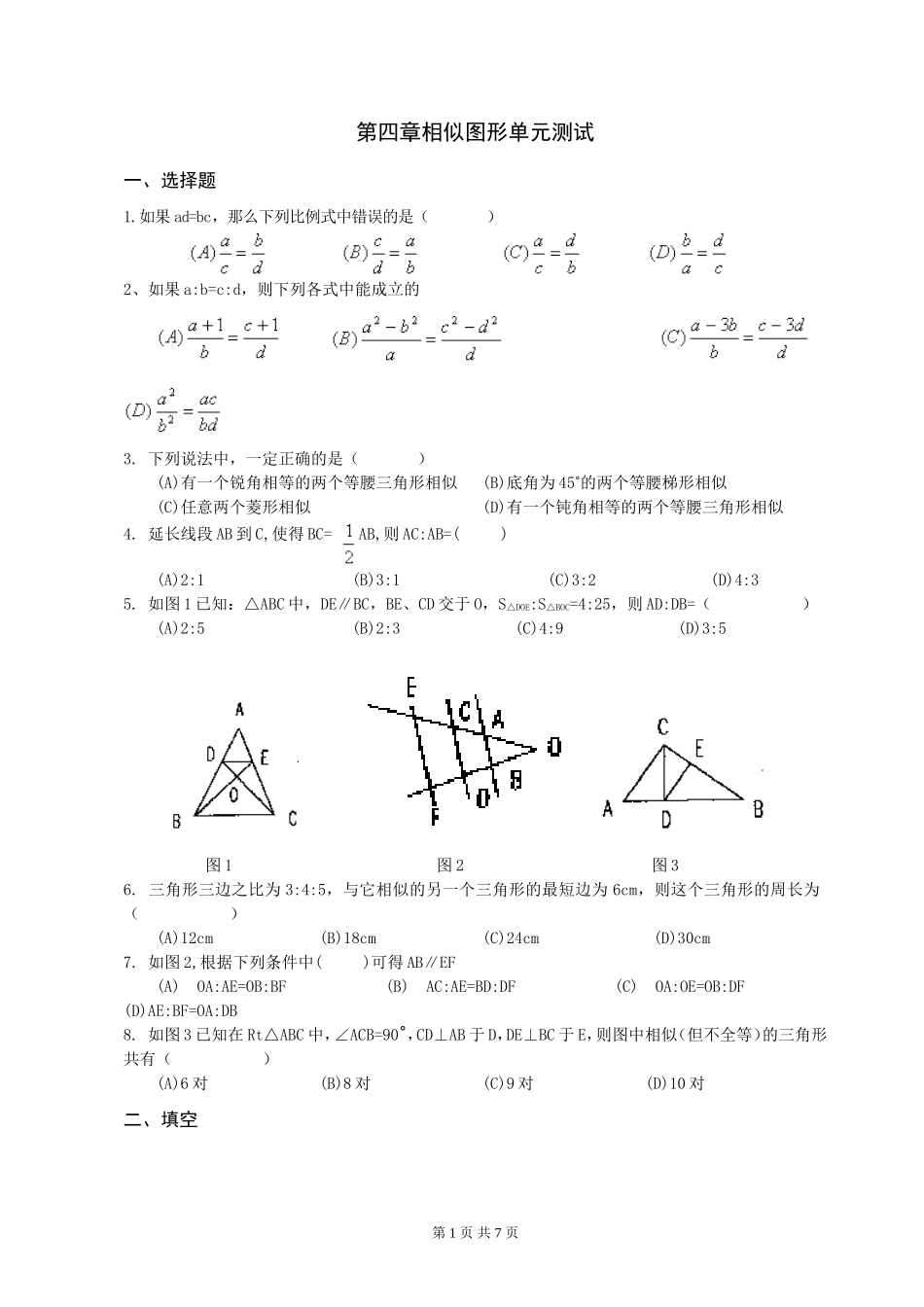
第四章相似图形单元测试一、选择题1.如果ad=bc,那么下列比例式中错误的是()2、如果a:b=c:d,则下列各式中能成立的3.下列说法中,一定正确的是()(A)有一个锐角相等的两个等腰三角形相似(B)底角为45˚的两个等腰梯形相似(C)任意两个菱形相似(D)有一个钝角相等的两个等腰三角形相似4.延长线段AB到C,使得BC=AB,则AC:AB=()(A)2:1(B)3:1(C)3:2(D)4:35.如图1已知:△ABC中,DE∥BC,BE、CD交于O,S△DOE:S△BOC=4:25,则AD:DB=()(A)2:5(B)2:3(C)4:9(D)3:5图1图2图36.三角形三边之比为3:4:5,与它相似的另一个三角形的最短边为6cm,则这个三角形的周长为()(A)12cm(B)18cm(C)24cm(D)30cm7.如图2,根据下列条件中()可得AB∥EF(A)OA:AE=OB:BF(B)AC:AE=BD:DF(C)OA:OE=OB:DF(D)AE:BF=OA:DB8.如图3已知在Rt△ABC中,∠ACB=90˚,CD⊥AB于D,DE⊥BC于E,则图中相似(但不全等)的三角形共有()(A)6对(B)8对(C)9对(D)10对二、填空第1页共7页1.如果,则,。2在比例尺为1:50000的地图上,一图形的周长为20cm,面积为50cm,那么此图形的实际周长为m;实际面积为千米2。3.在比例尺是1:10000的地图上,图距25mm,则实距是;如果实距为500m,其图距为cm4.已知,则5.两个相似多边形面积之比为3:4,则它们的相似比为_____。6.顺次连结三角形三边中点所成的三角形面积与原三角形面积之比为_____。7.直角三角形两直角边的比为2:3,则斜边上的高把斜边分成较长线段与较短线段的比为___。8.两个相似三角形对应高的比为1:√2,则它们的周长之比为________;面积之比为___。9.已知:x:y:z=3:4:5,且x+y-z=6,则:2x-3y+2z=_____10.如果△ABC∽△ADE,且∠C=∠AED,那么它们的对应边的比例式为。11.如图已知:△ABC中,DE∥BC,,则,。12.已知线段c是线段a和x的比例中项,则x=________;如果线段b是线段a、x、x的第四比例项,a=2,b=8,则x________。三、解答题xkb1.com1.如图已知:△ABC中,DE∥BC,DE=8,BC=12,AN⊥BC交DE于M,四边形BCED的面积为90。求:△ADE的面积及AM、AN的长。2.如图已知:△ABC中,F分AC为1:2两部分,D为BF中点,AD的延长线交BC于E.求:BE:EC第2页共7页四、证明题b1.com新课标第一网1.已知:菱形ABCD中,E为BC边上一点,AE交BD于F,交DC的延长线于G。求证:2.△ABC中,D为BC中点,过D的直线交AC于E,交AB的延长线于F。求证:3.△ABC中,D为BC中点,过D的直线交AC于E,交BA的延长线于F.求证:4.已知:求证:(1)(2)第3页共7页参考答案和评分标准一.选择题(本大题共32分)xkb1.com1C2C3D4C5B6C7A8C二.填空题(本大题共12分)新课标第一网1.:10000,12.52.250m,53.4.5.√3:26:1:4,7:9:4,81:√2,1:2981011第4页共7页12c2/a,4三.解答题(本大题共16分)1.:解:DE∥BC,△ADE∽△ABCS△ADE=x,S△ABC=x+90x=72S△ADE=72DE•AM=72AM=12AN=18答:△ADE的面积为72,AM=12,AN=182.:解:过F作FG∥BE交AD于G,则:∠GFD=∠EBDFG/EC=AF/AC=1/3在△BED和△FGD中,∠EBD=∠FGDBD=FD∠BDE=∠FDG△BED≌△FGD(ASA)BE=FGBE/EC=AF/AC=1/3四.证明题(本大题共40分)1.:证明:BE∥AD,∴又 AB∥DG,∴而AB=AD,∴即:2.:证明:在Rt△ABC中,CD⊥AB∴△ADC∽△CDB,∴即CD2=AD•BD ∠E+∠EAD=90˚,∠ABG+∠EAD=90˚∴∠E=∠ABG,即:∠E=∠DBF∴Rt△AED∽Rt△FBD∴,即:ED•FD=AD•BD第5页共7页∴CD2=ED•FD3.:证明:过B作BG∥AC交DF于G,则:∠GBD=∠C在△GBD和△ECD中∠GBD=∠C∠BDG=∠CDEBD=CD∴△GBD≌△ECD(AAS)∴BG=EC,∴4.:证明:过B作BG∥AC,则:∠GBD=∠C在△GBD和△ECD中,∠GBD=∠C(已证)BD=CD(中点性质)∠BDG=∠CDE(对顶角)∴△GBD≌△ECD(ASA)∴BG=EC∴5.:证明:设:则:a=bk,c=dk(1)(2)第6页共7页命题意图说明:《标准》在总体目标中提出“课程内容的学习,强调学生的数学活动,发展学生的数感、符号感、空间观念、统计观念、以及应用意识和推理能力”。数学的核心内容是初中学生应该掌握的学习内容,也是学生进一步发展的基础。因此本次期末评价立足考查学生对数感、符号感的领悟程度,考查学生的基本数学素养。体现基础性:试题题目首先要突出“双基”的考查,严格依据《标准》进行考核,试题的难、中、易比例为1...