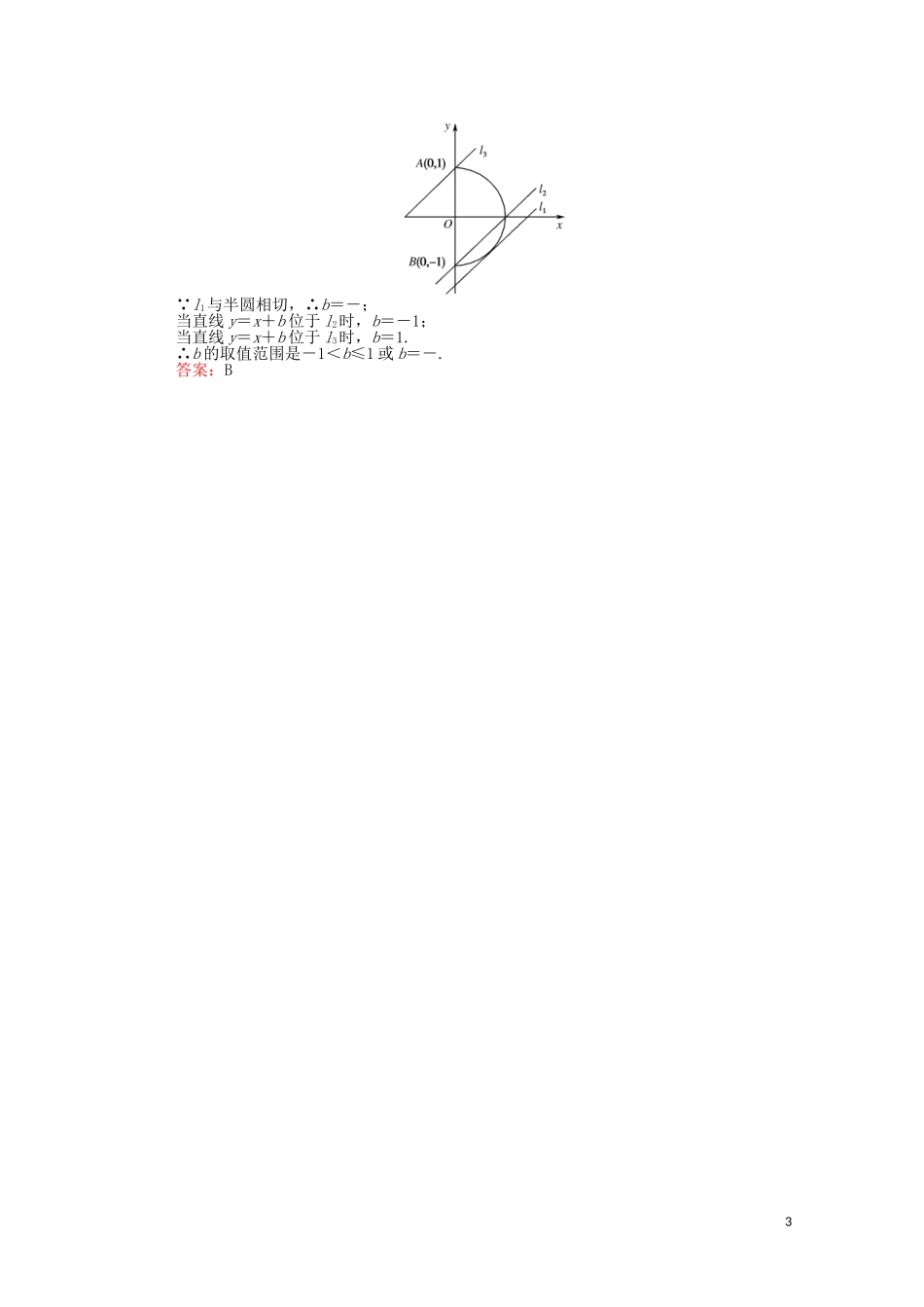
课时作业(十六)直线与圆的位置关系一、选择题1.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是()A.过圆心B.相切C.相离D.相交但不过圆心2.若直线y=x+a与圆x2+y2=1相切,则a的值为()A.B.±C.1D.±13.直线l:y-1=k(x-1)和圆x2+y2-2y=0的关系是()A.相离B.相切或相交C.相交D.相切4.若PQ是圆x2+y2=9的弦,PQ的中点是A(1,2),则直线PQ的方程是()A.x+2y-3=0B.x+2y-5=0C.2x-y+4=0D.2x-y=0二、填空题5.由点P(1,3)引圆x2+y2=9的切线段的长是________.6.若直线x-2y-3=0与圆C:(x-2)2+(y+3)2=9交于E,F两点,则△ECF的面积为________.7.圆x2+y2+2x+4y-3=0上到直线x+y+1=0的距离为的点有________个.三、解答题8.已知圆C:(x-1)2+(y-2)2=2,过点P(2,-1)作圆C的切线,切点为A,B.求直线PA,PB的方程.9.已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点.(1)求圆A的方程;(2)当|MN|=2时,求直线l的方程.[尖子生题库]10.直线y=x+b与曲线x=有且仅有一个公共点,则实数b的取值范围是()A.b=B.-1<b≤1或b=-C.-1≤b≤1D.以上都不正确1课时作业(十六)直线与圆的位置关系1.解析:圆心(1,-1)到直线3x+4y+12=0的距离d==<r.答案:D2.解析:由题意得=1,所以a=±,故选B.答案:B3.解析:l过定点A(1,1),∵12+12-2×1=0,∴点A在圆上,∵直线x=1过点A且为圆的切线,又l斜率存在,∴l与圆一定相交,故选C.答案:C4.解析:结合圆的几何性质知直线PQ过点A(1,2),且和直线OA垂直,故其方程为:y-2=-(x-1),整理得x+2y-5=0.答案:B5.解析:点P到原点O的距离为|PO|=,∵r=3,且P在圆外,∴切线段长为=1.答案:16.解析:圆心C(2,-3)到直线x-2y-3=0的距离为d==,又知圆C的半径长为3,∴|EF|=2=4,∴S△ECF=·|EF|·d=×4×=2.答案:27.解析:圆的方程可化为(x+1)2+(y+2)2=8,所以弦心距为d==.又圆的半径为2,所以到直线x+y+1=0的距离为的点有3个.答案:38.解析:切线的斜率存在,设切线方程为y+1=k(x-2),即kx-y-2k-1=0.圆心到直线的距离等于,即=,∴k2-6k-7=0,解得k=7或k=-1,故所求的切线方程为y+1=7(x-2)或y+1=-(x-2),即7x-y-15=0或x+y-1=0.9.解析:(1)设圆A的半径为r,∵圆A与直线l1:x+2y+7=0相切,∴r==2,∴圆A的方程为(x+1)2+(y-2)2=20.(2)当直线l与x轴垂直时,则直线l的方程x=-2,此时有|MN|=2,即x=-2符合题意.当直线l与x轴不垂直时,设直线l的斜率为k,则直线l的方程为y=k(x+2),即kx-y+2k=0,∵Q是MN的中点,∴AQ⊥MN,∴|AQ|2+2=r2,又∵|MN|=2,r=2,∴|AQ|==1,解方程|AQ|==1,得k=,∴此时直线l的方程为y-0=(x+2),即3x-4y+6=0.综上所述,直线l的方程为x=-2或3x-4y+6=0.10.解析:如图,作半圆的切线l1和经过端点A,B的直线l3,l2,由图可知,当直线y=x+b为直线l1或位于l2和l3之间(包括l3,不包括l2)时,满足题意.2∵l1与半圆相切,∴b=-;当直线y=x+b位于l2时,b=-1;当直线y=x+b位于l3时,b=1.∴b的取值范围是-1<b≤1或b=-.答案:B3