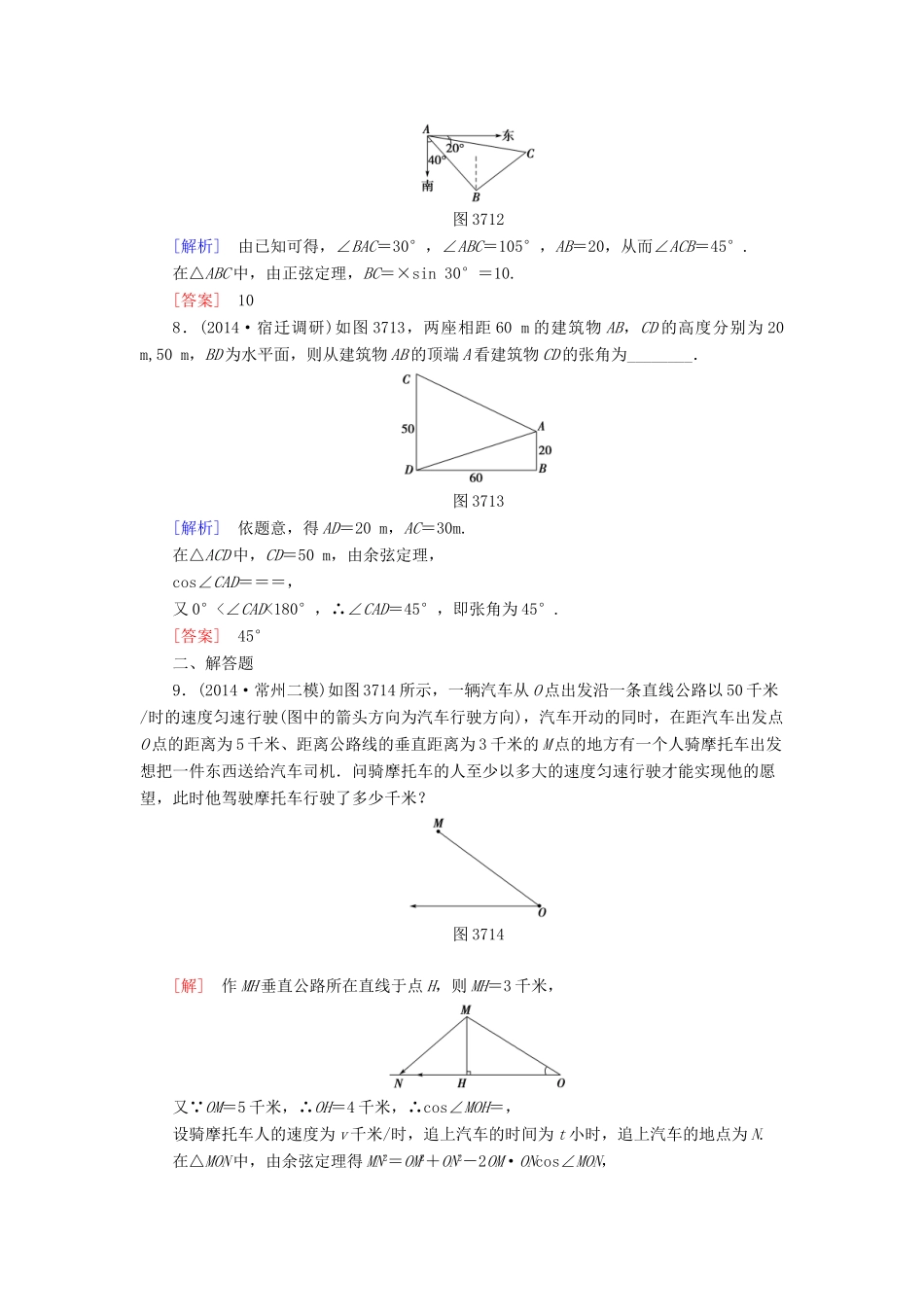
【高考讲坛】2016届高考数学一轮复习第3章第7节正弦定理、余弦定理的应用举例课后限时自测理苏教版[A级基础达标练]一、填空题1.两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站北偏东40°,灯塔B在观察站南偏东60°,则灯塔A在灯塔B的________.①北偏东10°;②北偏西10°;③南偏东10°;④南偏西10°[解析]灯塔A,B的相对位置如图所示,由已知得∠ACB=80°,∠CAB=∠CBA=50°,则α=60°-50°=10°即北偏西10°.[答案]②2.已知两座灯塔A、B与C的距离都是a,灯塔A在C的北偏东20°,灯塔B在C的南偏东40°,则灯塔A与灯塔B的距离为________.[解析]如图所示,由余弦定理可知,AB2=a2+a2-2a·a·cos120°=3a2得AB=a.[答案]a3.三角形的一边长为14,这条边所对的角为60°,另两边长之比为8∶5,则这个三角形的面积为________.[解析]设另两边长为8x与5x,则cos60°=,解得x=2,两边长为16与10,所以此三角形的面积为×16×10sin60°=×16×10×=40.[答案]404.一船向正北方向航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°方向,另一灯塔在船的南偏西75°方向,则这只船的速度是________海里/小时.[解析]如图所示,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10,在直角三角形ABC中,可得AB=5,于是这只船的速度是10海里/小时.[答案]105.(2014·广州调研)如图3711所示,长为3.5m的木棒AB斜靠在石堤旁,木棒的一端A在离堤足C处1.4m的地面上,另一端B在离堤足C处2.8m的石堤上,石堤的倾斜角为α,则坡度值tanα=________m.图3711[解析]由题意,在△ABC中,AB=3.5m,AC=1.4m,BC=2.8m且∠α+∠ACB=π由余弦定理得AB2=AC2+BC2-2AC·BC·cos∠ACB,即3.52=1.42+2.82-2×1.4×2.8×cos(π-α).∴cosα=(计算有技巧:等式两边同除以0.72).∴sinα=,∴tanα==.[答案]6.某人站在60米高的楼顶A处测量电视塔的高度,测得塔顶C的仰角为30°,塔底B的俯角为15°,已知楼底部D和电视塔的底部B在同一水平面上,则电视塔的高度为________米.[解析]如图所示,用AD表示楼高,BC表示塔高,设AE与水平面平行,E在线段BC上,因为∠CAE=30°,∠BAE=15°,AD=BE=60,则AE===120+60,在Rt△AEC中,CE=AE·tan30°=(120+60)×=60+40.所以电视塔的高度为60+40+60=(120+40)米.[答案]120+407.(2014·常州模拟)一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处.在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点距离为________海里.图3712[解析]由已知可得,∠BAC=30°,∠ABC=105°,AB=20,从而∠ACB=45°.在△ABC中,由正弦定理,BC=×sin30°=10.[答案]108.(2014·宿迁调研)如图3713,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角为________.图3713[解析]依题意,得AD=20m,AC=30m.在△ACD中,CD=50m,由余弦定理,cos∠CAD===,又0°<∠CAD<180°,∴∠CAD=45°,即张角为45°.[答案]45°二、解答题9.(2014·常州二模)如图3714所示,一辆汽车从O点出发沿一条直线公路以50千米/时的速度匀速行驶(图中的箭头方向为汽车行驶方向),汽车开动的同时,在距汽车出发点O点的距离为5千米、距离公路线的垂直距离为3千米的M点的地方有一个人骑摩托车出发想把一件东西送给汽车司机.问骑摩托车的人至少以多大的速度匀速行驶才能实现他的愿望,此时他驾驶摩托车行驶了多少千米?图3714[解]作MH垂直公路所在直线于点H,则MH=3千米,又 OM=5千米,∴OH=4千米,∴cos∠MOH=,设骑摩托车人的速度为v千米/时,追上汽车的时间为t小时,追上汽车的地点为N.在△MON中,由余弦定理得MN2=OM2+ON2-2OM·ONcos∠MON,即(vt)2=52+(50t)2-2×5×50t×,∴v2=-+2500=252+900,∴当t=时,v取得最大值30,其行驶距离为vt==千米故骑摩托车的人至少以30千米/时的速度行驶才能实现...