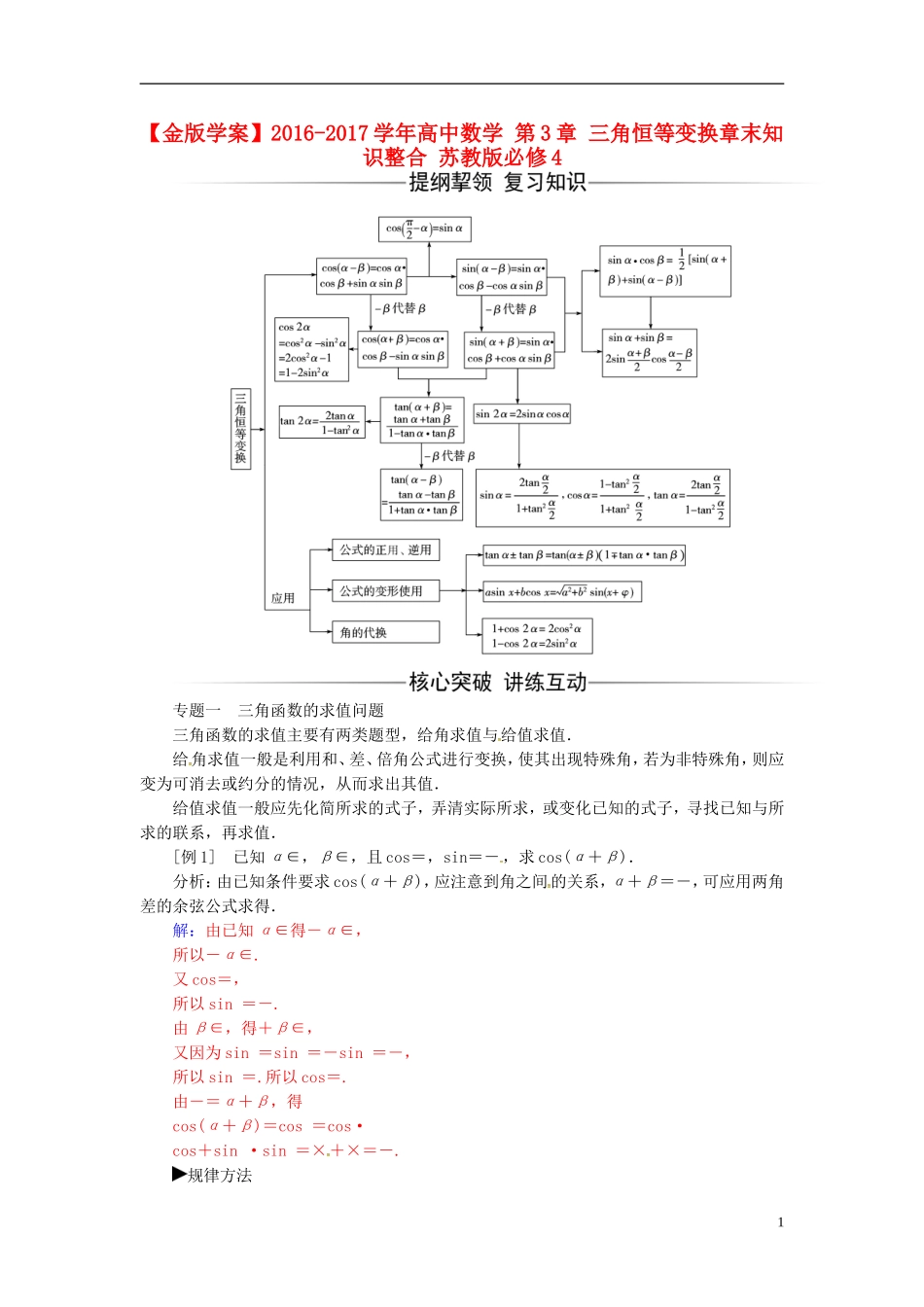
【金版学案】2016-2017学年高中数学第3章三角恒等变换章末知识整合苏教版必修4专题一三角函数的求值问题三角函数的求值主要有两类题型,给角求值与给值求值.给角求值一般是利用和、差、倍角公式进行变换,使其出现特殊角,若为非特殊角,则应变为可消去或约分的情况,从而求出其值.给值求值一般应先化简所求的式子,弄清实际所求,或变化已知的式子,寻找已知与所求的联系,再求值.[例1]已知α∈,β∈,且cos=,sin=-,求cos(α+β).分析:由已知条件要求cos(α+β),应注意到角之间的关系,α+β=-,可应用两角差的余弦公式求得.解:由已知α∈得-α∈,所以-α∈.又cos=,所以sin=-.由β∈,得+β∈,又因为sin=sin=-sin=-,所以sin=.所以cos=.由-=α+β,得cos(α+β)=cos=cos·cos+sin·sin=×+×=-.规律方法1给值求值的关键是找出已知式与欲求式之间的差异,一般可以适当变换已知式,求得另外函数式的值,以备应用,同时也要变换欲求式,便于将已知式求得的函数值代入,从而达到解题的目的.[变式训练]已知cos(α+β)=,cos(α-β)=,求tanα·tanβ的值.解:因为cos(α+β)=cosαcosβ-sinαsinβ=,①cos(α-β)=cosαcosβ+sinαsinβ=,②①+②得cosαcosβ=,②-①得sinαsinβ=-,所以tanαtanβ===-.[典例2]求sin220°+cos280°+sin20°cos80°的值.解:法一:原式=(1-cos40°)+(1+cos160°)+·(sin100°-sin60°)=1+(cos160°-cos40°)+sin100°-=-sin100°sin60°+sin100°=.法二:原式=sin220°+cos2(60°+20°)+sin20°·cos(60°+20°)=sin220°++sin20°·=sin220°+cos220°=.规律方法“给角求值”问题,一般所给出的角都是非特殊角,从表面上看是很难的,但仔细观察非特殊角与特殊角总有一定的关系,解题时,要认真观察,综合三角公式转化为特殊角并且清除非特殊角的三角函数而得解.[变式训练]求的值.解:原式======-4.专题二三角函数的化简三角函数式的化简是三角变换应用的一个重要方面,其基本思想方法是统一角、统一三角函数的名称.在具体实施过程中,应着重抓住“角”的统一.通过观察角、函数名、项的次数等,找到突破口,利用切化弦、升幂、降幂、逆用公式等手段将其化简.最后结果要求:(1)能求值尽量求值;(2)三角函数名称尽量少;(3)项数尽量少;(4)次数尽量低;(5)分母、根号下尽量不含三角函数.[典例3]化简:tan70°cos10°·(tan20°-1).分析:先化切为弦,再利用特殊角的特殊值进行转换.解:tan70°cos10°·(tan20°-1)=·cos10°·=cos10°-cos10°·=cos10°-====-1.规律方法在三角变换中,有时根据需要,可以将一特殊值还原成某一三角函数值,如:=sin=cos;1=tan=sin=cos=sin2α+cos2α等,如果我们在解题时巧妙地加以运用,往往会出奇制胜.[变式训练]化简(0<α<π).解:原式===,又0<α<π,知0<<,所以sin>0.2因此原式==-cosα.专题三三角恒等式的证明三角恒等式的证明主要有两种类型:绝对恒等式与条件恒等式.证明绝对恒等式要根据等式两边的特征,采取化繁为简,左右归一,变更命题等方法,通过三角恒等变换,使等式的两边化异为同.条件恒等式的证明则要认真观察、比较已知条件与求证等式之间的联系,选择适当途径,常用代入法、消去法、两头凑法等.[典例3]tanx-tan=.证明:左边=-====右边.即等式成立.规律方法证明三角恒等式,一般是从左证右或从右证左,或是两边分头化简得同一结果.同时要注意“切割化弦”“化异为同”基本原则的应用.[变式训练]求证:+=.证明:左边=+=+===右边.因此,原等式成立.专题四三角恒等变换的综合应用[典例4]已知函数f(x)=4cosωx·sin(ω>0)的最小正周期为π.(1)求ω的值;(2)讨论f(x)在区间上的单调性.分析:先利用两角和的正弦公式,再利用倍角公式“降次”,进而利用辅助角公式,化为一个角的一种三角函数的形式求解.解:(1)f(x)=4cosωx·sin=2sinωx·cosωx+2cos2ωx=(sin2ωx+cos2ωx)+=2sin+.因为f(x)的最小正周期为...