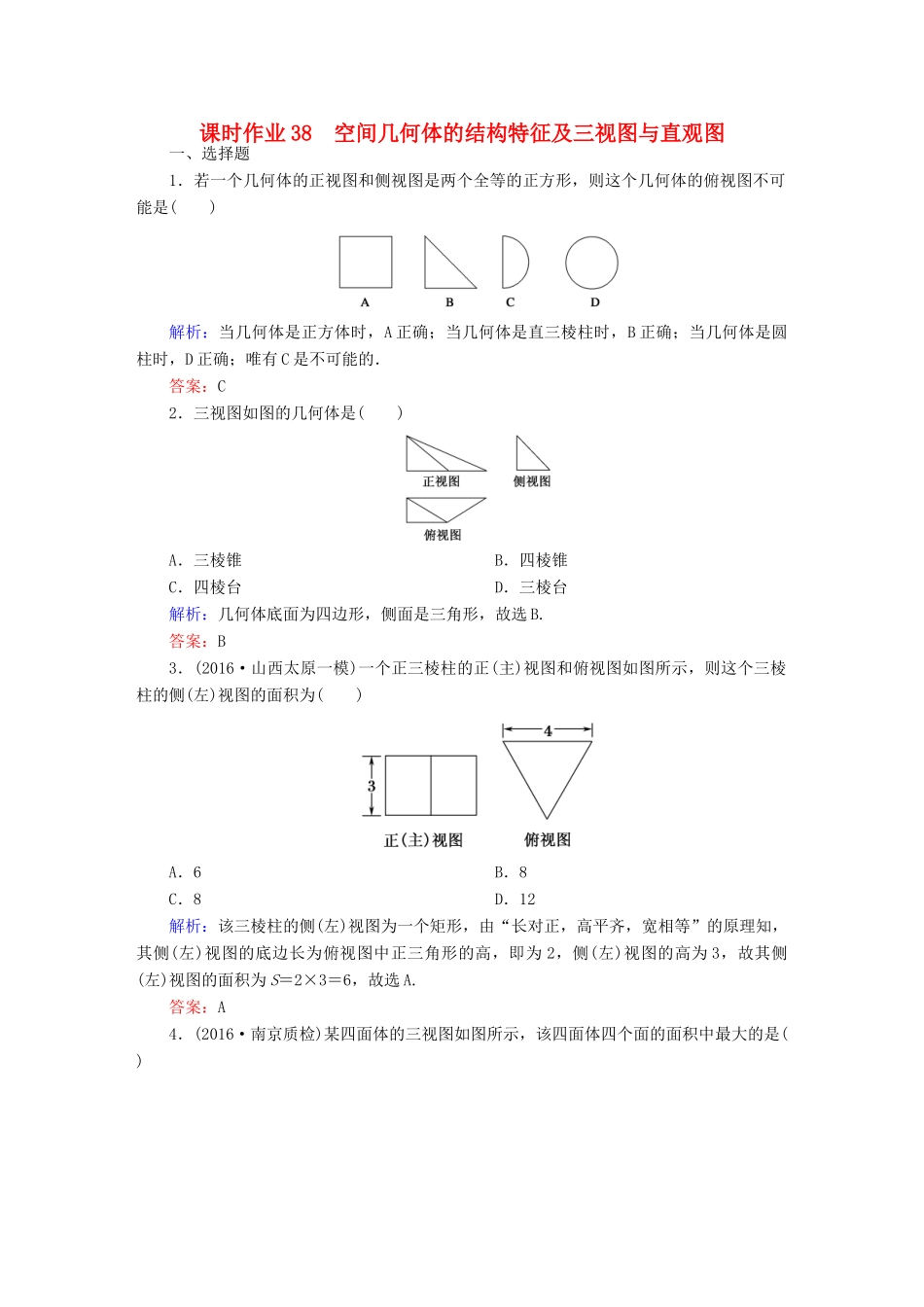
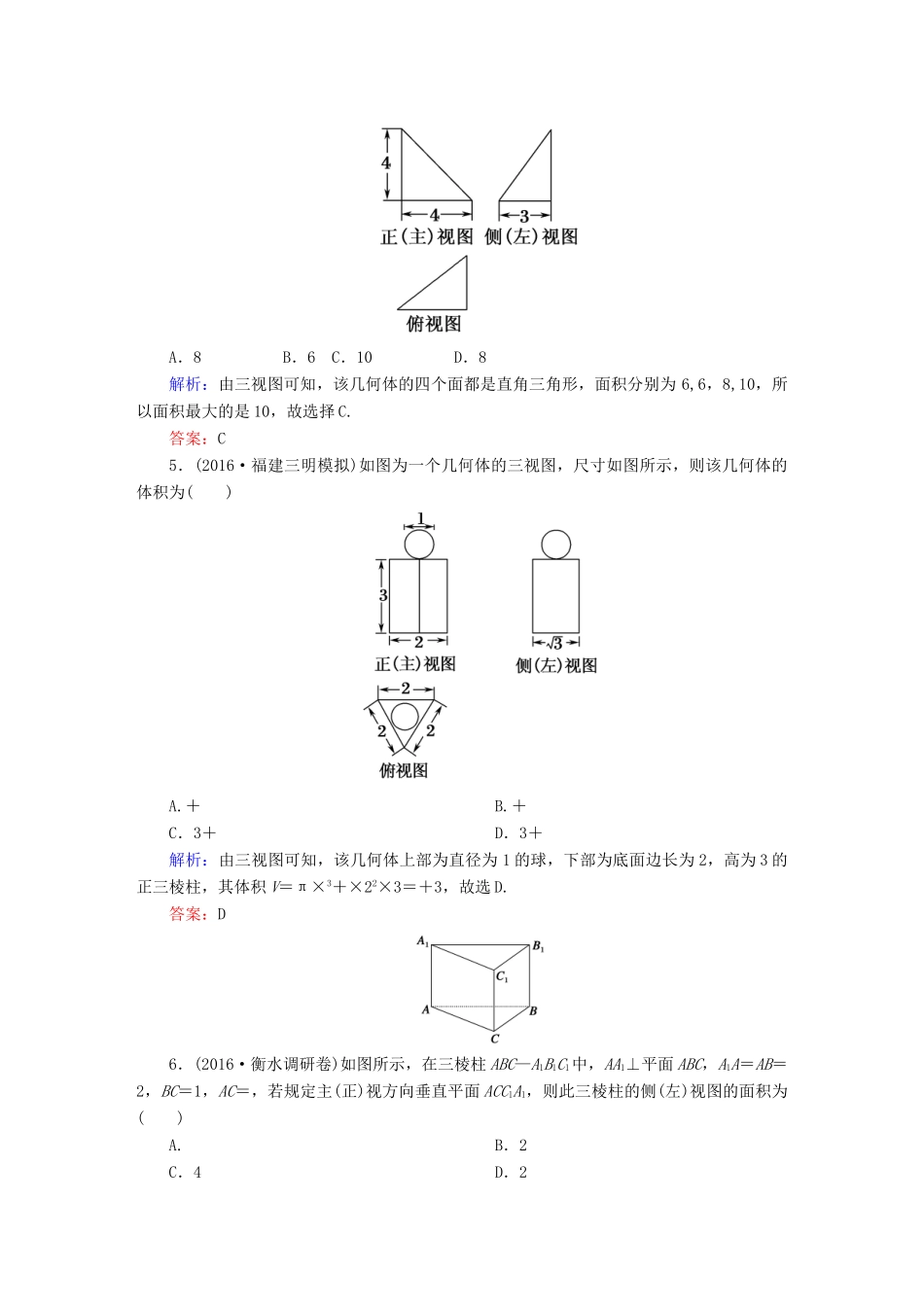
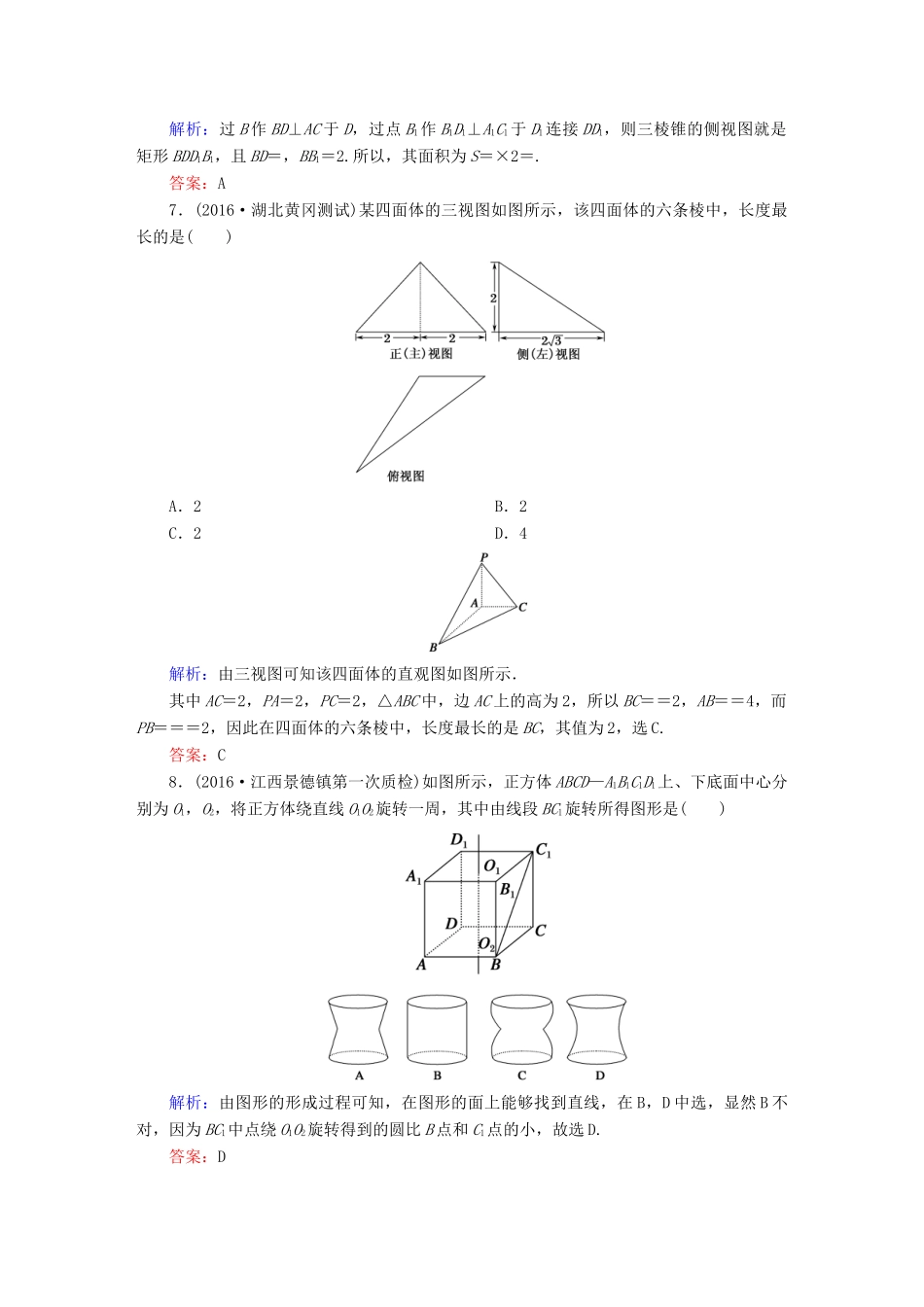
课时作业38空间几何体的结构特征及三视图与直观图一、选择题1.若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是()解析:当几何体是正方体时,A正确;当几何体是直三棱柱时,B正确;当几何体是圆柱时,D正确;唯有C是不可能的.答案:C2.三视图如图的几何体是()A.三棱锥B.四棱锥C.四棱台D.三棱台解析:几何体底面为四边形,侧面是三角形,故选B.答案:B3.(2016·山西太原一模)一个正三棱柱的正(主)视图和俯视图如图所示,则这个三棱柱的侧(左)视图的面积为()A.6B.8C.8D.12解析:该三棱柱的侧(左)视图为一个矩形,由“长对正,高平齐,宽相等”的原理知,其侧(左)视图的底边长为俯视图中正三角形的高,即为2,侧(左)视图的高为3,故其侧(左)视图的面积为S=2×3=6,故选A.答案:A4.(2016·南京质检)某四面体的三视图如图所示,该四面体四个面的面积中最大的是()A.8B.6C.10D.8解析:由三视图可知,该几何体的四个面都是直角三角形,面积分别为6,6,8,10,所以面积最大的是10,故选择C.答案:C5.(2016·福建三明模拟)如图为一个几何体的三视图,尺寸如图所示,则该几何体的体积为()A.+B.+C.3+D.3+解析:由三视图可知,该几何体上部为直径为1的球,下部为底面边长为2,高为3的正三棱柱,其体积V=π×3+×22×3=+3,故选D.答案:D6.(2016·衡水调研卷)如图所示,在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,A1A=AB=2,BC=1,AC=,若规定主(正)视方向垂直平面ACC1A1,则此三棱柱的侧(左)视图的面积为()A.B.2C.4D.2解析:过B作BD⊥AC于D,过点B1作B1D1⊥A1C1于D1连接DD1,则三棱锥的侧视图就是矩形BDD1B1,且BD=,BB1=2.所以,其面积为S=×2=.答案:A7.(2016·湖北黄冈测试)某四面体的三视图如图所示,该四面体的六条棱中,长度最长的是()A.2B.2C.2D.4解析:由三视图可知该四面体的直观图如图所示.其中AC=2,PA=2,PC=2,△ABC中,边AC上的高为2,所以BC==2,AB==4,而PB===2,因此在四面体的六条棱中,长度最长的是BC,其值为2,选C.答案:C8.(2016·江西景德镇第一次质检)如图所示,正方体ABCD—A1B1C1D1上、下底面中心分别为O1,O2,将正方体绕直线O1O2旋转一周,其中由线段BC1旋转所得图形是()解析:由图形的形成过程可知,在图形的面上能够找到直线,在B,D中选,显然B不对,因为BC1中点绕O1O2旋转得到的圆比B点和C1点的小,故选D.答案:D9.(2016·河南郑州质检)某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy的最大值为()A.32B.32C.64D.64解析:由三视图知三棱锥如图所示,底面ABC是直角三角形,AB⊥BC,PA⊥平面ABC,BC=2,PA2+y2=102,(2)2+PA2=x2,因此xy=x=x≤=64,当且仅当x2=128-x2,即x=8时取等号,因此xy的最大值是64,选C.答案:C10.如图所示,在正方体ABCD—A′B′C′D′中,M,E是AB的三等分点,G,N是CD的三等分点,F,H分别是BC,MN的中点,则四棱锥A′—EFGH的侧视图为()解析:注意分清三等分点.可以看出,侧视图中A′E,A′G重合,A′H成为A′M,A′F,A′B重合,侧视图为向左倾斜的三角形,故选C.答案:C11.若一个几何体的三视图如下图所示,则该几何体的体积为()A.2B.1C.D.解析:由三视图知,该几何体是一棱锥,其底面四边形的对角线互相垂直,且长都为2,棱锥高为1,所以,该几何体的体积为V=×2××2×1=.答案:C12.(2016·贵州七校联考)如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)()A.①②⑥B.①②③C.④⑤⑥D.③④⑤解析:正视图应该是相邻两边长为3和4的矩形,其对角线左下到右上是实线,左上到右下是虚线,因此正视图是①;侧视图应该是相邻两边长为5和4的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此侧视图是②;俯视图应该是相邻两边长为3和5的矩形,其对角线左上到右下是实线,左下到右上是虚线,因此俯视图是③,故选B.答案:B二、填空题13.(2016·河北石家庄模拟)如图,矩形O′A′B′C′是水平放置的平面图形OABC的...