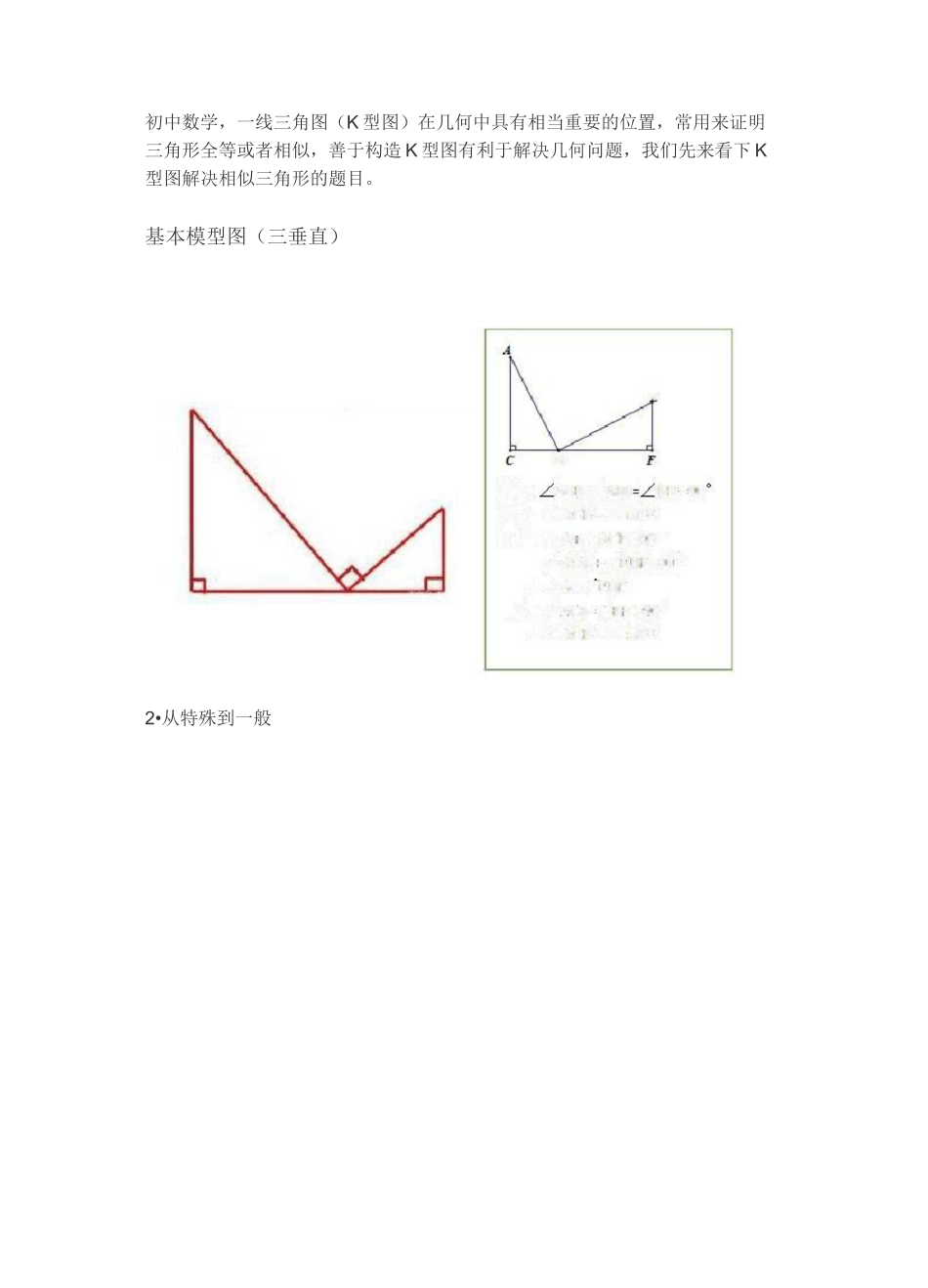
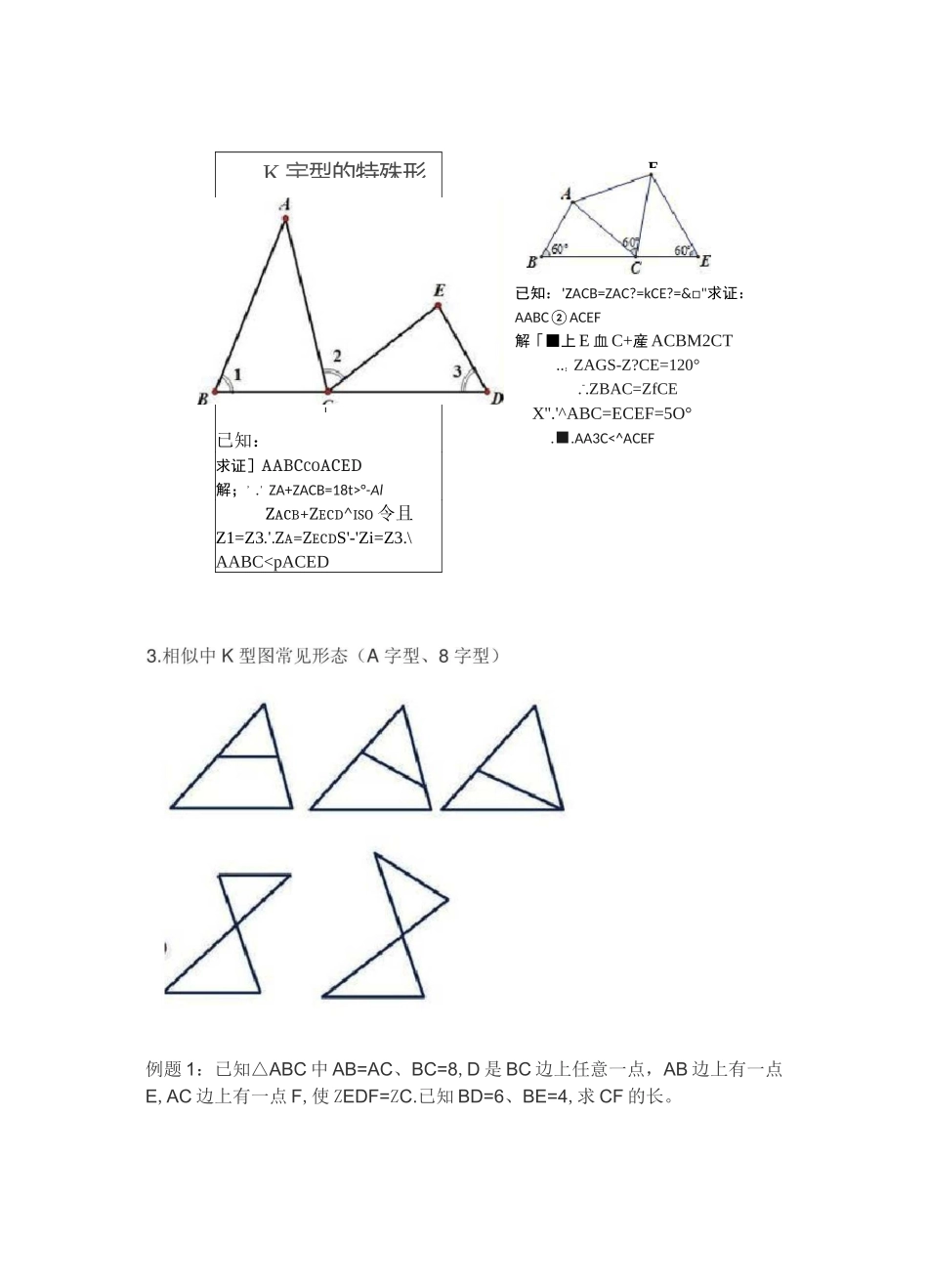
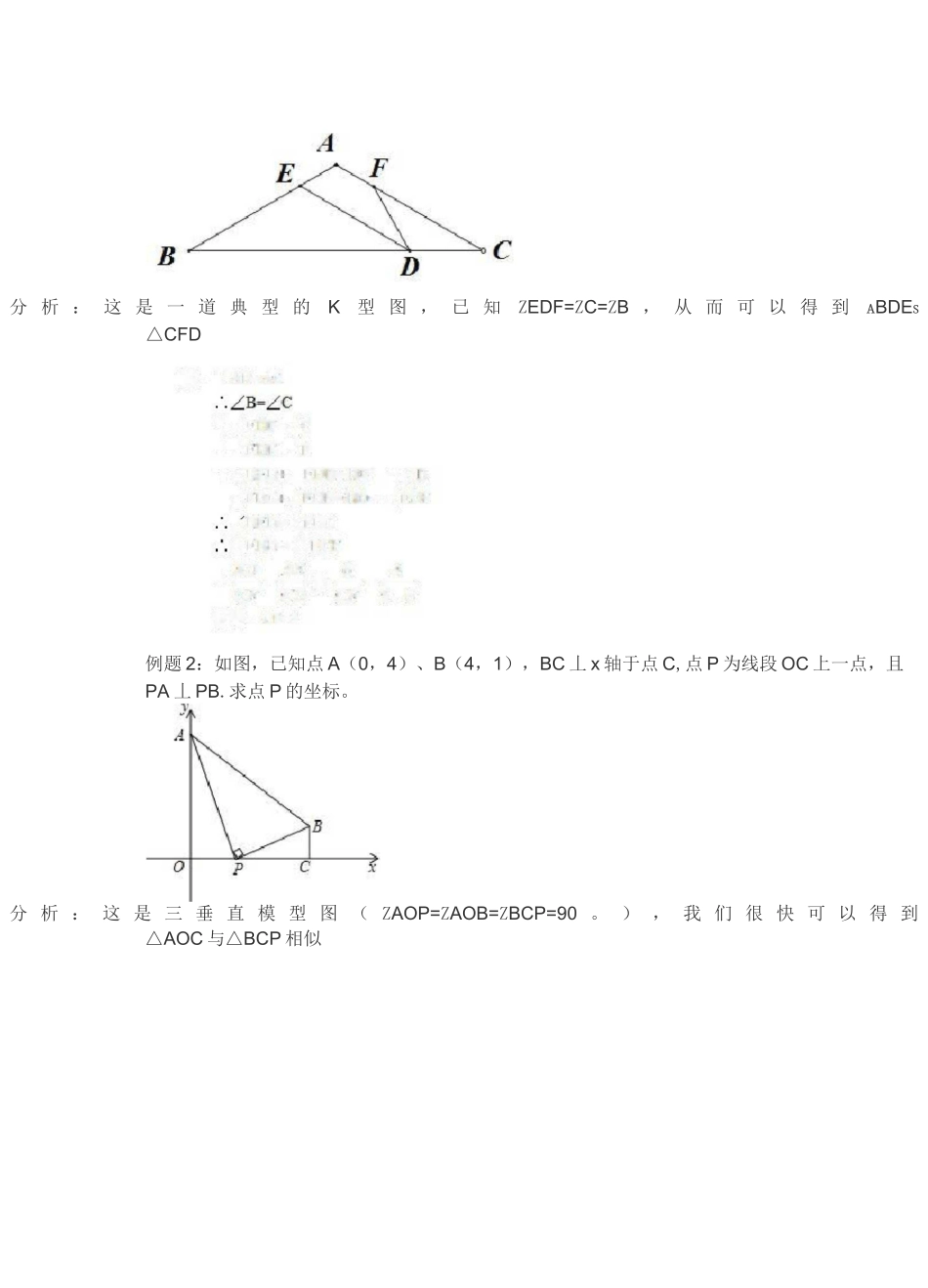
FB已知:.ACB=ZABEBFE^94)隶证:△NCBSZYBFE解;丁産遇一忆ACB-gtr厶CB-NE斑T虑-\ZA=.Z:EBF又■.'.ZACB-ZBFE-90^:..AACB■COABFE初中数学,一线三角图(K型图)在几何中具有相当重要的位置,常用来证明三角形全等或者相似,善于构造K型图有利于解决几何问题,我们先来看下K型图解决相似三角形的题目。基本模型图(三垂直)2•从特殊到一般K宇型的特殊形已知:求证]AABCCOACED解;,.,ZA+ZACB=18t>°-AlZACB+ZECD^ISO令且Z1=Z3.'.ZA=ZECDS'-'Zi=Z3.\AABC
ZFDCAEBIX^ADCF.・.NEDF=T感BEA/EDE=1$IT—ZE嚼哙即詁三;\'AB=A■/ZEDF=ZC分析:这是一道典型的K型图,已知ZEDF=ZC=ZB,从而可以得到ABDES△CFD例题2:如图,已知点A(0,4)、B(4,1),BC丄x轴于点C,点P为线段OC上一点,且PA丄PB.求点P的坐标。分析:这是三垂直模型图(ZAOP=ZAOB=ZBCP=90。),我们很快可以得到△AOC与△BCP相似B3囹OP4解得:0P=2,AP(2;0;如圈i所示iTgA丄P西,\Z2+Z3=90°』TAO丄X釉,.'.Z1=Z2,又\BC丄J(轴,AO丄鮮由,.■.(/BCP=^POA=gO°’t\OPAO■/*A(0,4)iBC4,1)*.+.AO=4,BC=1,OC=4,14-OP21)晋AE_APDP~D解析:由图可知:ZA=ZEPC=ZD=90°,是三垂直模型,可以得到AEAPS^PDC,通过比例式得到x与y的函数关系式,进而求出y的最大值舞:T四边^ABCD是鉅形F:AB-CD-2,=r.'.^AEP+ZAPE=-90DrZAEP-\-ZDPC=90ar3Q・5二牙时F的最大直雳r•■片_»十乞「222例题3:已知矩形ABCD中,CD=2,AD=3,点P是AD上的一个动点,且和点A,D不重合,过点P作PE丄CP,交边AB于点E,设PD=x,AE=y,求y关于x的函数关系式,并求出y的最大值。EECEC5丄.等聘山BS近心g,厶410*琢的中点「小藕皇看含曲箱的透明三角断便30诵的顶点薄在占、比三角転建P点稚轻.CL)如■團召.当三角柯的两边分另咬Afl*AC于点桑F时.求证:ASPECTAcFP;C2)^m:将三雷皈统点F碳话到凰t■惜瞄时,三甬板餉輛边汗囲咬臥的延长线、迪忆于点E、F.01M1:ADFI与妝丹还齟似吧?(只恚写出结论)0採究E:蓬詰EFj3FE£aTE罡否抑卿请说朋理却®设EEL,血肝商面枳为力试用丹的惑式未示a2.已知JE册AKD的一憑边就观特匡鬆A0CD抵鼠使得顶査B藩在CD边上的F点粧・6ESIS2CD忆图片已如折瘪芍边BC交干点4连结會、朋、0A.<0求证:△OCPSKPD们②若皿防与AF加的面积比为If4,求边AE的长$CE)若囲1申朝点.F恰妤罡CDJS的中点」求/豳的戾SL⑶如凰劭程⑴秦潮J愉却?纟緞朗,连结BF・讪点」在瓣殳fiP上■(点H与点T*A不重知「动点N莅线番AB的睡也岂虹■旦测讦片扇聊交冷于点黔作ME丄弱于点匸试I请当小N在移动过程申'综段EF脱農是否岌生凭化¥若愛化,说明理由|着不变,求出结段EF的烁.c471F]已知正方形AECD的边长为4.—于以点止为哂点的暫角端点A旅转”竜囱两边汾别与边眈、X的延畏言汝于占氏F,理接Ehi^CE-a,CF-b.COSG®1-当上EAT視对角线见C平分时.求比D的向⑵当AAEF良直角三甬飛旳卜菠氛b的值:3)如團採慕点AF绕点4庇帏的讨瑋中Xt满足的关系式,并说明理由.4I電读理鮮i如團1,左四边形鮎①的边期上任取一点Et点E不与触氏至合》•分别连接脱酹可以杷四酬呦分廡三个三甬俐山口果耳中育两个三弟飛柏f忙珈il就把E叫做四边形JffiCP的边坨上的“啊脯"、堆果遼三今戸甬形剽目佻搁I]斓巴E叫做四边形阳3的边出上的“强相佩.护.網九何題;⑴如闽厶=4虫磁W,试蒯点E是否是四迪形避口的边伍上的相他点.,并说明理由*(2)如團2,在疫形ABCfrIp,A.B,C.D四梆■瘫正方时网洛〔网格中昌牛小正方形的边长九1)的格点£即曲个沪正方牌的顶点)上,试柱圉2中画出鉅形ABCD的边AB上僦相佩点1⑶如厢典瘠狂昭ABCL沿CH折鼠使点B時在AB也上的点巨处■苦点E恰妊厦匾2(备頁圉①園②團③呈四曲形AK1的边M上的T强相饥审」试摄究扯与號的数量关系1•由“一线三直角”基本图形搭建桥梁可以得到相似三角形。2•学习几何最重要是学会归纳一些简单的基本图形,学会从复杂的图形里提炼基本图形,并将其作为解决问题的手段和方法。3•几何的学习中,要注重图形的运动和变化,总结和发现图形之间的内在联系,探求其规律,帮我们解决繁杂问题