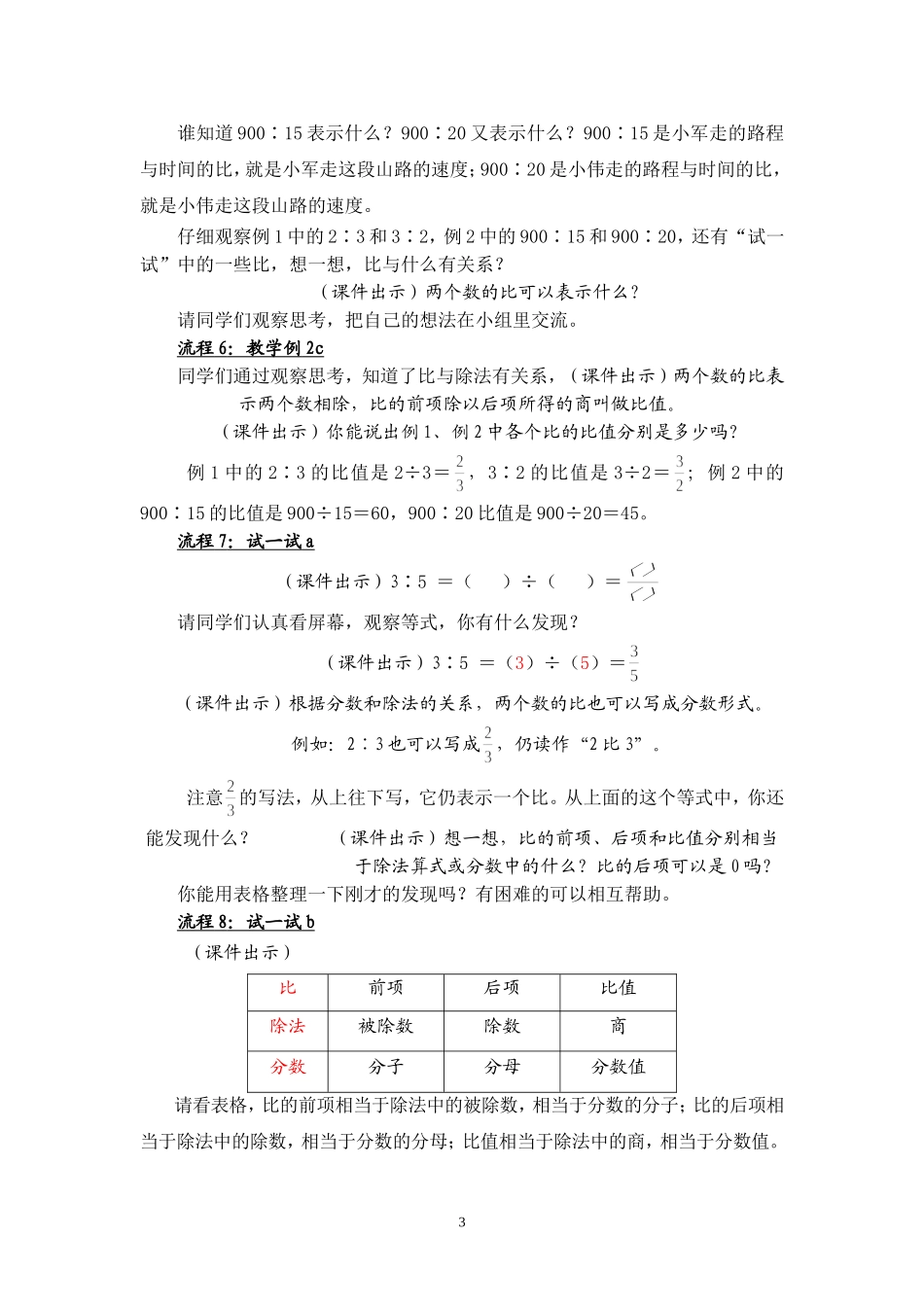
比的意义巢湖市城北小学丁雪松简要提示苏教版小学数学六年级上册,教科书p68-p70例1、例2及相应的“试一试”“练一练“,练习十三第1-5题。这节课通过教学,使学生理解比的意义,学会比的读写法,认识比的各部分名称;掌握求比值的方法,会正确求比值;弄清比同除法、分数的关系,明白比的后项不能是零的道理,同时懂得事物之间是相互联系的。第一段:教学例1、例2和“试一试”师:同学们,妈妈早晨准备了2杯果汁和3杯牛奶,请看屏幕!流程1:教学例1a(课件:图)例1妈妈早晨准备了2杯果汁和3杯牛奶。“2杯果汁”和“3杯牛奶”这两个数量之间有什么样的关系?你会用哪些方法表示它们的关系?(课件出示)可以怎样表示这两个数量之间的关系?表示“2杯果汁”和“3杯牛奶”这两个数量之间的关系,可以这样说:(课件出示)牛奶比果汁多1杯,相差关系果汁的杯数相当于牛奶的,倍数关系果汁比牛奶少1杯。牛奶的杯数相当于果汁的。表示两个数量之间的关系,我们已会用减法比较两个数量之间的相差关系,也会用分数或除法比较两个数量之间的倍比关系。其实,两个数量之间的关系还可以用一种新的方法表示。这就是我们今天要学习的新知识──比。用比怎样表示“2杯果汁”和“3杯牛奶”这两个数量之间的关系呢?请同1学们认真阅读课本第68页图下面的一段话,看谁能独立弄懂这部分内容。流程2:教学例1b(课件:删上2句)这两个数量之间的关系还可以说成:果汁与牛奶杯数的比是2比3;牛奶与果汁杯数的比是3比2。2比3记作2∶3;3比2记作3∶2。“∶”是比号,比号前面的数叫做比的前项,比号后面的数叫做比的后项请同学们注意:两个数的比是有顺序的,颠倒两个数量的位置,就会得出另外一个比,其意义也就不同。因此,要按照叙述的顺序,搞清楚是哪个量与哪个量相比。如“果汁与牛奶杯数的比是2∶3”而“牛奶与果汁杯数的比是3∶2”。其实,比表示的就是两个数量之间的倍数关系,如,果汁与牛奶杯数的比是2∶3,可以理解为果汁有2份,牛奶有3份;也可以理解为果汁的杯数相当于牛奶的,牛奶的杯数相当于果汁的。流程4:教学例2a(课件出示)例2走一段900米长的山路,小军用了15分,小伟用了20分。分别算出他们的速度,填入下表。路程时间速度小军900米15分小伟900米20分请同学们打开书第69页看例2表格,分别填写出小军和小伟的速度。(课件出示)路程时间速度小军900米15分60米/分小伟900米20分45米/分同学们填写表格计算速度,是根据速度=路程÷时间。速度实际上表示了路程和时间的关系,我们也可以用比来表示路程和时间的这种关系。(课件出示)速度=路程÷时间,也可以用比来表示路程和时间的关系你能试着写一写小军和小伟,他们每人所走路程与时间的比吗?有困难的同学可以先看一看课本第69页表格下面的一段话。流程5:教学例2b(课件出示)小军走的路程与时间的比是900∶15;小伟走的路程与时间的比是900∶20。2谁知道900∶15表示什么?900∶20又表示什么?900∶15是小军走的路程与时间的比,就是小军走这段山路的速度;900∶20是小伟走的路程与时间的比,就是小伟走这段山路的速度。仔细观察例1中的2∶3和3∶2,例2中的900∶15和900∶20,还有“试一试”中的一些比,想一想,比与什么有关系?(课件出示)两个数的比可以表示什么?请同学们观察思考,把自己的想法在小组里交流。流程6:教学例2c同学们通过观察思考,知道了比与除法有关系,(课件出示)两个数的比表示两个数相除,比的前项除以后项所得的商叫做比值。(课件出示)你能说出例1、例2中各个比的比值分别是多少吗?例1中的2∶3的比值是2÷3=,3∶2的比值是3÷2=;例2中的900∶15的比值是900÷15=60,900∶20比值是900÷20=45。流程7:试一试a(课件出示)3∶5=()÷()=请同学们认真看屏幕,观察等式,你有什么发现?(课件出示)3∶5=(3)÷(5)=(课件出示)根据分数和除法的关系,两个数的比也可以写成分数形式。例如:2∶3也可以写成,仍读作“2比3”。注意的写法,从上往下写,它仍表示一个比。从上面的这个等式中,你还能发现什么?(课件出示)想一想,比的前项、后项和比值分别相当于除法算式或分数中...