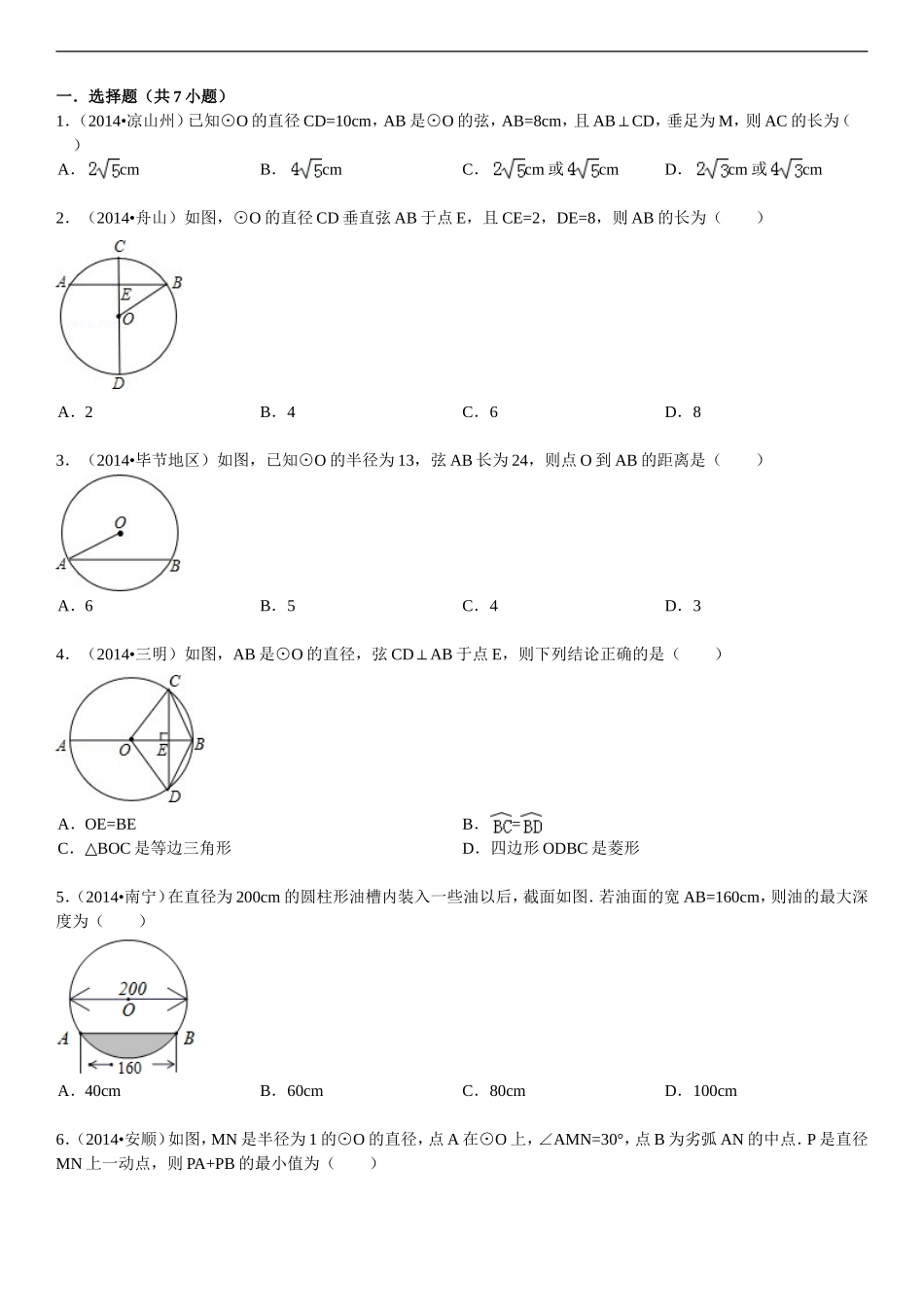
一.选择题(共7小题)1.(2014•凉山州)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且ABCD⊥,垂足为M,则AC的长为()A.cmB.cmC.cm或cmD.cm或cm2.(2014•舟山)如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为()A.2B.4C.6D.83.(2014•毕节地区)如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是()A.6B.5C.4D.34.(2014•三明)如图,AB是⊙O的直径,弦CDAB⊥于点E,则下列结论正确的是()A.OE=BEB.=C.BOC△是等边三角形D.四边形ODBC是菱形5.(2014•南宁)在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为()A.40cmB.60cmC.80cmD.100cm6.(2014•安顺)如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为()A.B.1C.2D.27.(2014•沛县模拟)如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A的坐标是()A.(5,4)B.(4,5)C.(5,3)D.(3,5)二.解答题(共7小题)8.(2014•佛山)如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.9.(2014•盘锦三模)如图,CD为⊙O的直径,CDAB⊥,垂足为点F,AOBC⊥,垂足为E,,(1)求AB的长;(2)求⊙O的半径.10.(2009•长宁区二模)如图,点C在⊙O的弦AB上,COAO⊥,延长CO交⊙O于D.弦DEAB⊥,交AO于F.(1)求证:OC=OF;(2)求证:AB=DE.11.(2009•浦东新区二模)一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.(1)求此时的水深(即阴影部分的弓形高);(2)当水位上升到水面宽为0.8米时,求水面上升的高度.12.(2008•长宁区二模)如图,在△ABC中,AB=AC,⊙O过点B、C,且交边AB、AC于点E、F,已知∠A=ABO∠,连接OE、OF、OB.(1)求证:四边形AEOF为菱形;(2)若BO平分∠ABC,求证:BE=BC.13.(2007•佛山)如图,⊙O是△ABC的外接圆,且AB=AC=13,BC=24,求⊙O的半径.14.(2007•青浦区二模)如图,一条公路的转弯处是一段圆弧(图中的弧AB),点O是这段弧的圆心,点C是弧AB上的一点,OCAB⊥,垂足为D,如AB=60m,CD=10m,求这段弯路的半径.参考答案与试题解析一.选择题(共7小题)1.(2014•凉山州)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且ABCD⊥,垂足为M,则AC的长为()A.cmB.cmC.cm或cmD.cm或cm考点:垂径定理;勾股定理.菁优网版权所有专题:分类讨论.分析:先根据题意画出图形,由于点C的位置不能确定,故应分两种情况进行讨论.解答:解:连接AC,AO,O ⊙的直径CD=10cm,ABCD⊥,AB=8cm,AM=∴AB=×8=4cm,OD=OC=5cm,当C点位置如图1所示时,OA=5cm ,AM=4cm,CDAB⊥,OM=∴==3cm,CM=OC+OM=5+3=8cm∴,AC=∴==4cm;当C点位置如图2所示时,同理可得OM=3cm,OC=5cm ,MC=53=2cm∴﹣,在RtAMC△中,AC===2cm.故选:C.点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.2.(2014•舟山)如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为()A.2B.4C.6D.8考点:垂径定理;勾股定理.菁优网版权所有专题:计算题.分析:根据CE=2,DE=8,得出半径为5,在直角三角形OBE中,由勾股定理得BE,根据垂径定理得出AB的长.解答:解: CE=2,DE=8,OB=5∴,OE=3∴,ABCD ⊥,∴在△OBE中,得BE=4,AB=2BE=8∴.故选:D.点评:本题考查了勾股定理以及垂径定理,是基础知识要熟练掌握.3.(2014•毕节地区)如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是()A.6B.5C.4D.3考点:垂径定理;勾股定理.菁优网版权所有分析:过O作OCAB⊥于C,根据垂径定理求出AC,根据勾股定理求出OC即可.解答:解:过O作OCAB⊥于C,OC 过O,AC=BC=∴AB=12,在RtAOC△中,由勾股定理得:OC==5.故选:B.点评:本题考查了垂径定理和勾股定理的应用,关键是求出OC的长.4.(2014•三明)如图,AB是⊙O的直径,弦CDAB⊥于...