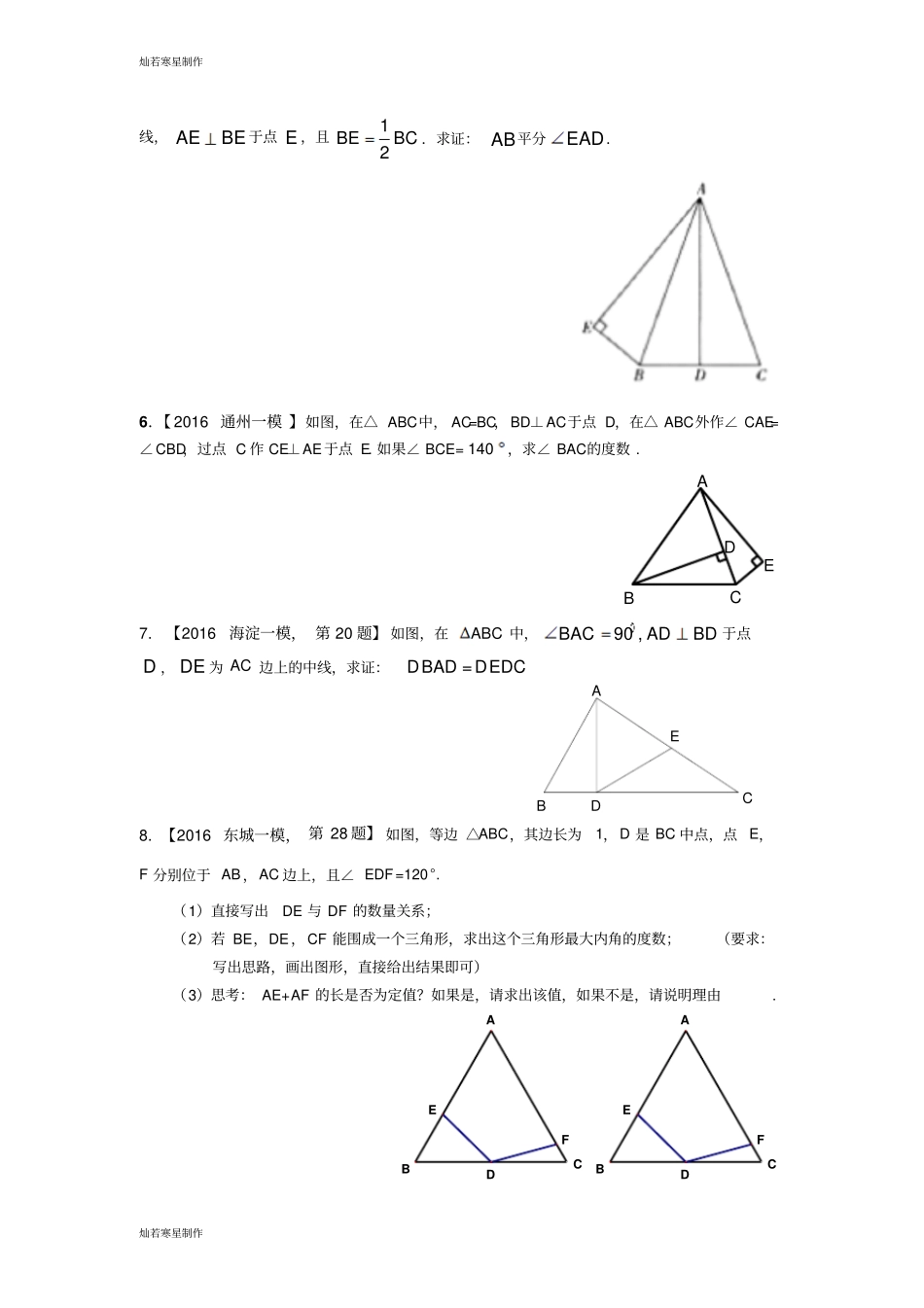
灿若寒星制作灿若寒星制作北京市2016年各区中考一模汇编平面几何之三角形1.【2016东城一模,第20题】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).2.【2016丰台一模,第20题】如图,在ABC中,AD是BC边上的高线,BEAC于点E,∠BAD=∠CBE.求证:ABAC3.【2016平谷一模,第20题】如图,△ABC中,AB=AC,点D是BC上一点,DE⊥AB于E,FD⊥BC于D,G是FC的中点,连接GD.求证:GD⊥DE4321AFBCDEG4.【2016朝阳一模,第20题】如图,E为AC上一点,EF∥AB交AF于点F,且AE=EF.求证:BAC=2∠1.1FECBA5.【2016西城一模,第19题】如图,在ABC中,ABAC,AD是BC边上的中灿若寒星制作灿若寒星制作线,AEBE于点E,且12BEBC.求证:AB平分EAD.6.【2016通州一模】如图,在△ABC中,AC=BC,BD⊥AC于点D,在△ABC外作∠CAE=∠CBD,过点C作CE⊥AE于点E.如果∠BCE=140,求∠BAC的度数.EDABC7.【2016海淀一模,第20题】如图,在ABC中,90,BACADBD于点D,DE为AC边上的中线,求证:DBAD=DEDCABDEC8.【2016东城一模,第28题】如图,等边△ABC,其边长为1,D是BC中点,点E,F分别位于AB,AC边上,且∠EDF=120°.(1)直接写出DE与DF的数量关系;(2)若BE,DE,CF能围成一个三角形,求出这个三角形最大内角的度数;(要求:写出思路,画出图形,直接给出结果即可)(3)思考:AE+AF的长是否为定值?如果是,请求出该值,如果不是,请说明理由.DCABEFDCABEF灿若寒星制作灿若寒星制作灿若寒星制作灿若寒星制作1.【2016东城一模,第20题】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠BAC=40°,请你选择图中现有的一个角并求出它的度数(要求:不添加新的线段,所有给出的条件至少使用一次).解:∠E=35°,或∠EAB=35°,或∠EAC=75°.⋯⋯⋯⋯1分 在△ABC中,AB=AC,∠BAC=40°,∴∠ABC=∠ACB=70°.⋯⋯⋯⋯3分又 BD平分∠ABC,∴∠ABD=∠CBD=35°.⋯⋯⋯⋯4分 AE∥BD,∴∠E=∠EAB=35°.⋯⋯⋯⋯5分∴∠EAC=∠EAB+∠BAC=75°.2.【2016丰台一模,第20题】如图,在ABC中,AD是BC边上的高线,BEAC于点E,∠BAD=∠CBE.求证:ABAC.证明: 在△ABC中,AD是BC边上的高线,BEAC于点E,∴∠ADB=∠BEC=90°.--------2分.∴∠ABC+∠BAD=∠C+∠CBE=90°.又 BADCBE,∴∠ABC=∠C.----------4分∴ABAC.------------5分3.【2016平谷一模,第20题】如图,△ABC中,AB=AC,点D是BC上一点,DE⊥AB于E,FD⊥BC于D,G是FC的中点,连接GD.求证:GD⊥DE.证明: AB=AC,∴∠B=∠C.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 DE⊥AB,FD⊥BC,∴∠BED=∠FDC=90°.∴∠1=∠3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 G是直角三角形FDC的斜边中点,∴GD=GF.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3∴∠2=∠3.∴∠1=∠2. ∠FDC=∠2+∠4=90°,∴∠1+∠4=90°.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4∴∠2+∠FDE=90°.∴GD⊥DE.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯54.【2016朝阳一模,第20题】如图,E为AC上一点,EF∥AB交AF于点F,且AE=EF.求证:BAC=2∠1.证明: EF∥AB,∴∠1=∠FAB.⋯⋯⋯⋯⋯⋯⋯⋯2分 AE=EF,1FECBA4321AFBCDEG灿若寒星制作灿若寒星制作∴∠EAF=∠EFA.⋯⋯⋯⋯⋯⋯3分 ∠1=∠EFA,∴∠EAF=∠1.⋯⋯⋯⋯⋯⋯⋯⋯4分∴∠BAC=2∠1.⋯⋯⋯⋯⋯⋯⋯5分5.【2016西城一模,第19题】如图,在ABC中,ABAC,AD是BC边上的中线,AEBE于点E,且12BEBC.求证:AB平分EAD.6.【2016通州一模】如图,在△ABC中,AC=BC,BD⊥AC于点D,在△ABC外作∠CAE=∠CBD,过点C作CE⊥AE于点E.如果∠BCE=140,求∠BAC的度数.解: BD⊥AC,CE⊥AE,∴90BDCE, ∠CAE=∠CBD,∴△BDC∽△AEC,⋯⋯⋯⋯⋯⋯⋯2分;∴∠BCD=∠ACE, ∠BCE=140,∴∠BCD=∠ACE=70,⋯⋯⋯⋯⋯⋯⋯4分; AC=BC,∴∠ABC=∠BAC=55.⋯⋯⋯⋯⋯⋯⋯5分.7.【2016海淀一模,第20题】如图,在ABC中,90,BACADBD于点D,DE为AC边上的中线,求证:DBAD=DEDCABDECEDABC灿若寒星制作灿若寒...