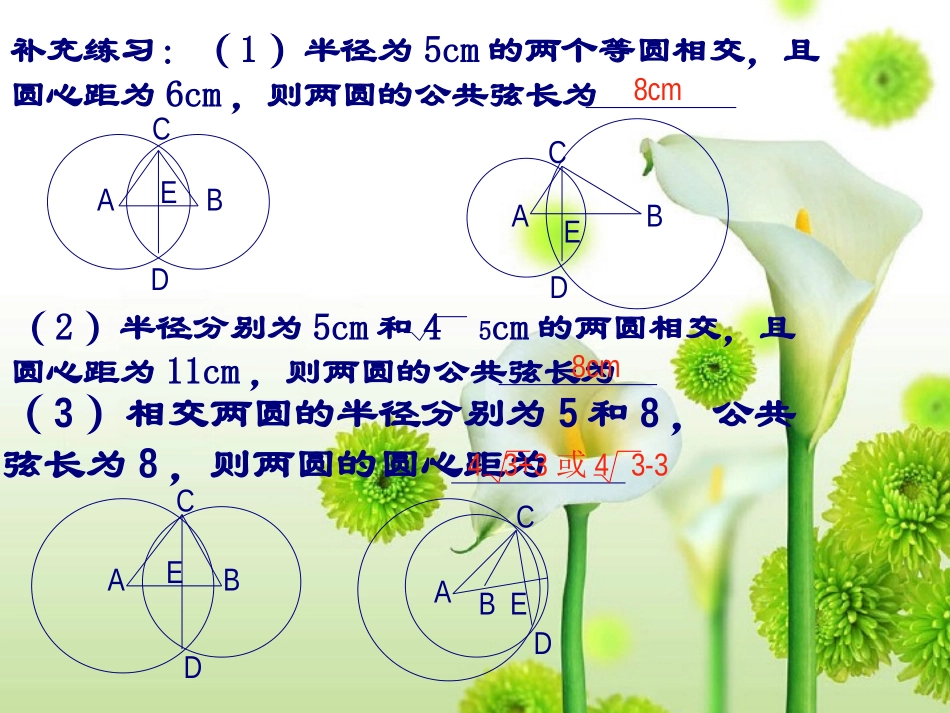
丹徒区宝堰中学胡斌观察思考:O1O2与AB有何数量关系和位置关系?为什么?.O1O2.AB定理1相交两圆的连心线垂直平分公共弦CDO1O2例1已知:如图,圆O1与圆O2相交于A、B,过点A的直线MN⊥AB,分别交两圆于点M、N。求证:MN=2O1O2ABMN注意:弦心距是常添的辅助线,它与弦构成“基本图形”练习:书本P971、2.(与例题比较方法上的相同点)(3)相交两圆的半径分别为5和8,公共弦长为8,则两圆的圆心距为补充练习:(1)半径为5cm的两个等圆相交,且圆心距为6cm,则两圆的公共弦长为ABCDECDABEABCDEABCDE8cm43+3或43-3(2)半径分别为5cm和45cm的两圆相交,且圆心距为11cm,则两圆的公共弦长为8cmo1po2..o2.po1.观察思考:此时的连心线有何特殊性?为什么?定理2相切两圆的连心线经过切点证明:假设点P不在连心线O1O2上,因为连心线O1O2是圆O1和O2的公共对称轴,所以点P的对称点P’也不在O1O2上,又因为点P是两圆的公共点,所以点P’也是两圆的公共点,即圆O1与圆O2有两个公共点,这与已知“圆O1与圆O2相切”矛盾所以切点P必在连心线O1O2上不直接从命题的条件推出结论,而是从结论的反面出发,引出矛盾,从而证明命题成立,这种证明的方法叫做反证法.用反证法证明命题一般有下面三个步骤:1.假设命题的结论不成立;2.从这个假设与已知条件出发,经过推理,得出矛盾;3.由矛盾判定假设不正确,从而肯定命题的结论成立.例4用反证法证明:过同一直线上的三点不能作圆.已知:点A,B,C在同一直线l上求证:过A,B,C三点不能作圆Oll1l2A.B..C练习:课本P98—991、2.课堂作业:课本P99习题6.7第3题