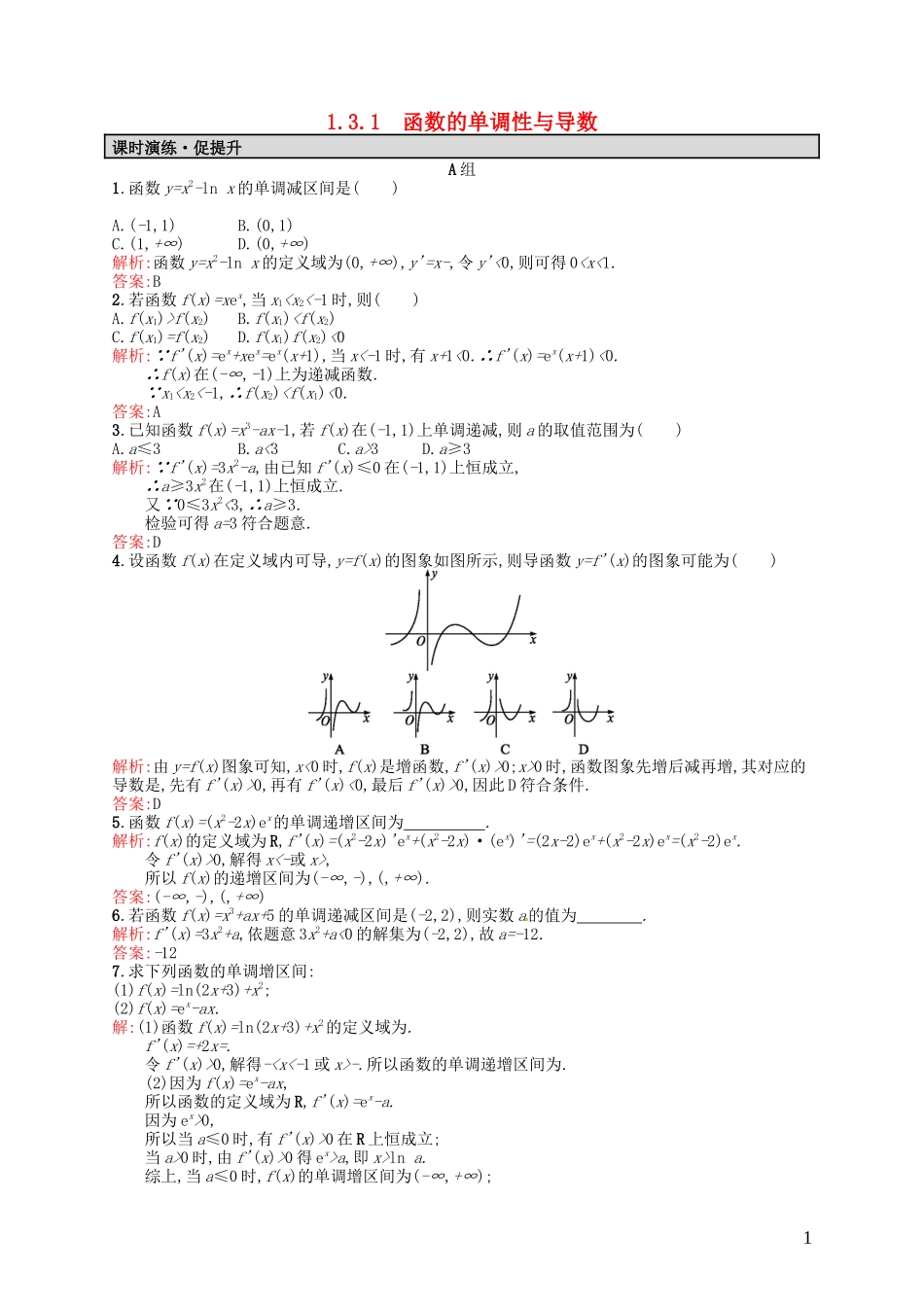
1.3.1函数的单调性与导数课时演练·促提升A组1.函数y=x2-lnx的单调减区间是()A.(-1,1)B.(0,1)C.(1,+∞)D.(0,+∞)解析:函数y=x2-lnx的定义域为(0,+∞),y'=x-,令y'<0,则可得0f(x2)B.f(x1)3D.a≥3解析:∵f'(x)=3x2-a,由已知f'(x)≤0在(-1,1)上恒成立,∴a≥3x2在(-1,1)上恒成立.又∵0≤3x2<3,∴a≥3.检验可得a=3符合题意.答案:D4.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f'(x)的图象可能为()解析:由y=f(x)图象可知,x<0时,f(x)是增函数,f'(x)>0;x>0时,函数图象先增后减再增,其对应的导数是,先有f'(x)>0,再有f'(x)<0,最后f'(x)>0,因此D符合条件.答案:D5.函数f(x)=(x2-2x)ex的单调递增区间为.解析:f(x)的定义域为R,f'(x)=(x2-2x)'ex+(x2-2x)·(ex)'=(2x-2)ex+(x2-2x)ex=(x2-2)ex.令f'(x)>0,解得x<-或x>,所以f(x)的递增区间为(-∞,-),(,+∞).答案:(-∞,-),(,+∞)6.若函数f(x)=x3+ax+5的单调递减区间是(-2,2),则实数a的值为.解析:f'(x)=3x2+a,依题意3x2+a<0的解集为(-2,2),故a=-12.答案:-127.求下列函数的单调增区间:(1)f(x)=ln(2x+3)+x2;(2)f(x)=ex-ax.解:(1)函数f(x)=ln(2x+3)+x2的定义域为.f'(x)=+2x=.令f'(x)>0,解得--.所以函数的单调递增区间为.(2)因为f(x)=ex-ax,所以函数的定义域为R,f'(x)=ex-a.因为ex>0,所以当a≤0时,有f'(x)>0在R上恒成立;当a>0时,由f'(x)>0得ex>a,即x>lna.综上,当a≤0时,f(x)的单调增区间为(-∞,+∞);1当a>0时,f(x)的单调增区间为(lna,+∞).8.已知函数f(x)=x2+(x≠0,常数a∈R).若函数f(x)在x∈[2,+∞)上是单调递增的,求a的取值范围.解:f'(x)=2x-.要使f(x)在[2,+∞)上是单调递增的,则f'(x)≥0在x∈[2,+∞)上恒成立,即≥0在x∈[2,+∞)上恒成立.∵x2>0,∴2x3-a≥0.∴a≤2x3在x∈[2,+∞)上恒成立.∴a小于2x3在定义域内的最小值.∵x∈[2,+∞),y=2x3是单调递增的,∴y=2x3在定义域内的最小值为16,∴a≤16.当a=16时,f'(x)=≥0(x∈[2,+∞))有且只有f'(2)=0,∴a的取值范围是a≤16.B组1.函数f(x)=ax3-x在R上为减函数,则()A.a≤0B.a<1C.a<2D.a≤解析:f'(x)=3ax2-1.∵f(x)在R上为减函数,∴f'(x)≤0在R上恒成立.∴a≤0,经检验a=0符合题意.答案:A2.设f(x),g(x)在[a,b]上可导,且f'(x)>g'(x),则当ag(x)B.f(x)g(x)+f(a)D.f(x)+g(b)>g(x)+f(b)解析:∵f'(x)-g'(x)>0,∴(f(x)-g(x))'>0,∴f(x)-g(x)在[a,b]上是增函数,∴当af(a)-g(a),∴f(x)+g(a)>g(x)+f(a).答案:C3.已知函数f(x)=在(-2,+∞)内单调递减,则实数a的取值范围为.解析:f'(x)=,由题意得f'(x)≤0在(-2,+∞)内恒成立,所以解不等式得a≤,但当a=时,f'(x)=0恒成立,不合题意,应舍去,所以a的取值范围是.答案:4.若函数f(x)=2x2-lnx在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围是.解析:因为f(x)的定义域为(0,+∞),又f'(x)=4x-,由f'(x)=0,得x=.据题意,解得1≤k<.答案:5.求证:当x>1时,x>ln(1+x).证明:设f(x)=x-ln(1+x)(x>1),则f'(x)=1-.∵当x>1时,f'(x)>0,∴f(x)在(1,+∞)上是增函数,∴当x>1时,f(x)=x-ln(1+x)>f(1)=1-ln2>1-lne=0,∴f(x)>0,即x>ln(1+x)(x>1).6.已知函数f(x)=lnx-ax2-2x存在单调递减区间,求a的取值范围.解:由f(x)=lnx-ax2-2x,x∈(0,+∞),所以f'(x)=-ax-2.因为f(x)在(0,+∞)上存在单调递减区间,所以当x∈(0,+∞)时,-ax-2<0有解,即a>有解.设G(x)=,所以只要a>G(x)min即可.而G(x)=-1,所以G(x)min=-1.所以a>-1,即a的取值范围是(-1,+∞).7.已知函数f(x)=mx3+nx2(m,n∈R,m≠0),函数y=f(x)的图象在点(2,f(2))处的切线与x轴平行.(1)用关于m的代数式表示n;2(2)求函数f(x)的单调增区间.解:(1)由已知条件得f'(x)=3mx2+2nx,又f'(2)=0,∴3m+n=0,故n=-3m.(2)∵n=-3m,∴f(x)=mx3-3mx2,∴f'(x)=3mx2-6mx.令f'(x)>0,即3mx2-6mx>0,当m>0时,解得x<0或x>2,则函数f(x)的单调增区间是(-∞,0)和(2,+∞);当m<0时,解得00时,函数f(x)的单调增区间是(-∞,0)和(2,+∞);当m<0时,函数f(x)的单调增区间是(0,2).3