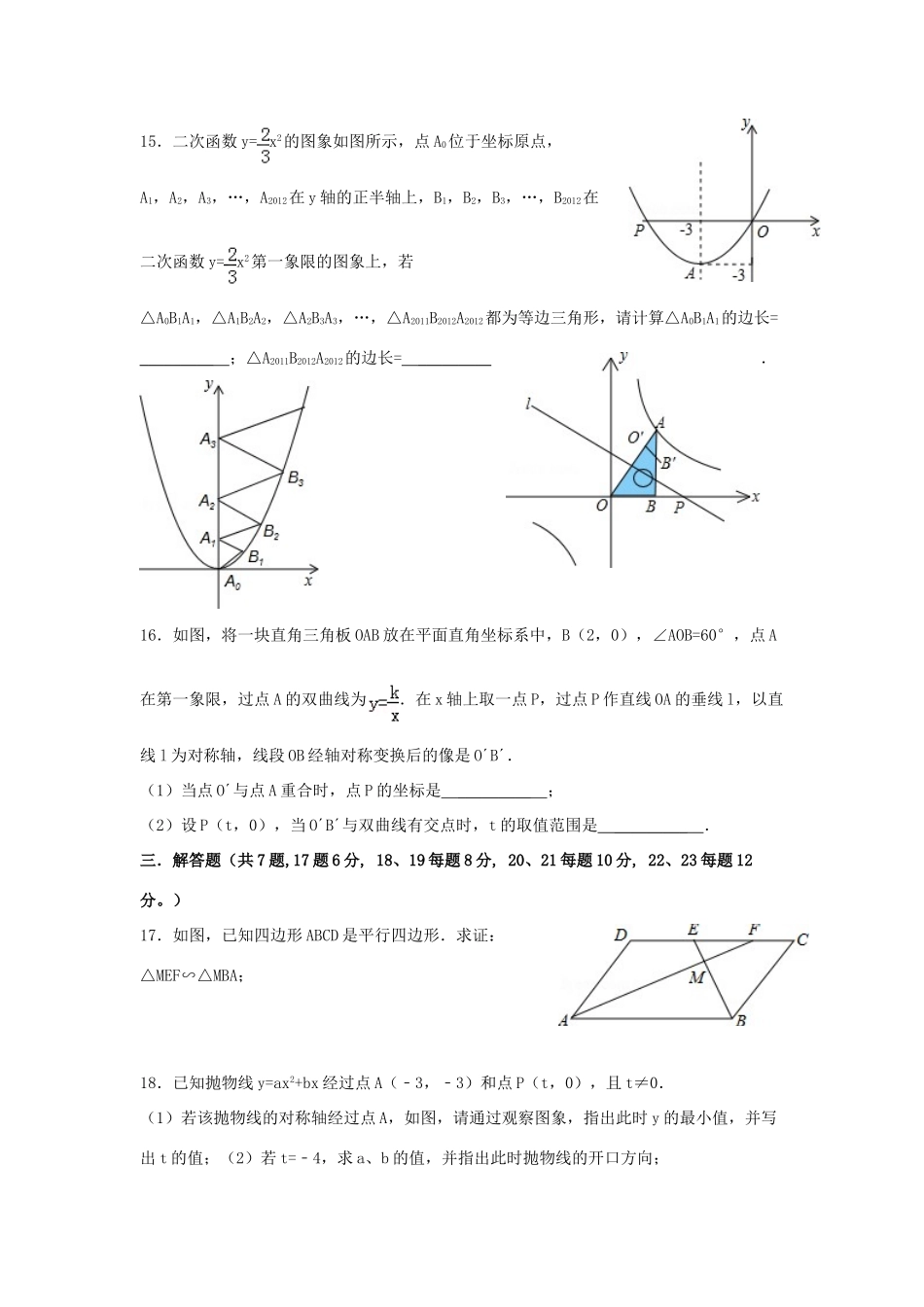
浙江省杭州市2013届九年级数学上学期教学质量检测试题(无答案)湘教版考时:100分钟分值:120分一.选择题(共10小题,每小题3分,共30分)1.若,则=()A.B.C.D.2.如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是()A.∠ABD=∠CB.∠ADB=∠ABCC.D.3.如图,正方形ABOC的边长为2,反比例函数的图象过点A,则k的值是()A.2B.﹣2C.4D.﹣44.如图,在⊙O中,弦AB∥CD,若∠ABC=40°,则∠BOD=()A.20°B.40°C.50°D.80°5.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为()A.πB.C.7πD.6π6.若二次函数y=x2+bx+5配方后为y=(x﹣2)2+k,则b、k的值分别为()A.0,5B.﹣4,1C.﹣4,5D.0,17.下列语句中,正确的有()个.(1)三点确定一个圆(2)平分弦的直径垂直于弦(3)相等的弦所对的弧相等(4)相等的圆心角所对的弧相等.A.0个B.1个C.2个D.3个8.如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连结EB、CA交于点F,则=()A.B.C.D.9.已知函数,并且是方程的两个根,则实数的大小关系可能是()A、B、C、D、10.一个正整数若能表示成两个正整数的平方差,则称这个正整数为“如意数”。例如,就是一个“如意数”。把所有的“如意数”从小到大排列后,第47个“如意数”是()A、97B、95C、65D、64二.填空题(共6小题,每小题4分,共24分)11.在一张比例尺为1:20的图纸上,某矩形零件的面积为12cm2;则这个零件的实际面积为cm2.12.圆锥底面半径为,母线长为2,它的侧面展开图的圆心角是_________.13.抛物线y=﹣x2+bx+c的部分图象如图所示,请写出与其关系式,图象相关的2个正确结论:_________(对称轴方程,图象与x正半轴,y轴交点坐标例外).14.如图,在一场羽毛球比赛中,站在场内M处的运动员林丹把球从N点击到了对方内的B点,已知网高OA=1.52米,OB=4米,OM=5米,则林丹起跳后击球点N离地面的距离NM=_________米.15.二次函数y=x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2012在y轴的正半轴上,B1,B2,B3,…,B2012在二次函数y=x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2011B2012A2012都为等边三角形,请计算△A0B1A1的边长=_________;△A2011B2012A2012的边长=_________.16.如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.(1)当点O´与点A重合时,点P的坐标是_________;(2)设P(t,0),当O´B´与双曲线有交点时,t的取值范围是_________.三.解答题(共7题,17题6分,18、19每题8分,20、21每题10分,22、23每题12分。)17.如图,已知四边形ABCD是平行四边形.求证:△MEF∽△MBA;18.已知抛物线y=ax2+bx经过点A(﹣3,﹣3)和点P(t,0),且t≠0.(1)若该抛物线的对称轴经过点A,如图,请通过观察图象,指出此时y的最小值,并写出t的值;(2)若t=﹣4,求a、b的值,并指出此时抛物线的开口方向;19.如图,水平放置的圆柱形水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(结果保留π)20.(1)在同一个圆中,两条弦相交,被交点分成的两条线段的积有什么关系?请利用左图试着证明.(2)利用(1)的结论,解决右图问题:AB为⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径R.21.如图,Rt△ABO的顶点A是双曲线与直线在第二象限的交点,AB⊥轴于B且.(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A,C的坐标以及△AOC的面积.22.如图,为圆O的直径,为弦,且,垂足为.(1)如果圆O的半径为4,,求的度数;(2)若点为半圆的中点,连结,.求证:平分;(3)在(1)的条件下,圆周上到直线距离为3的点有多少个?并说明理由.23.对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E....