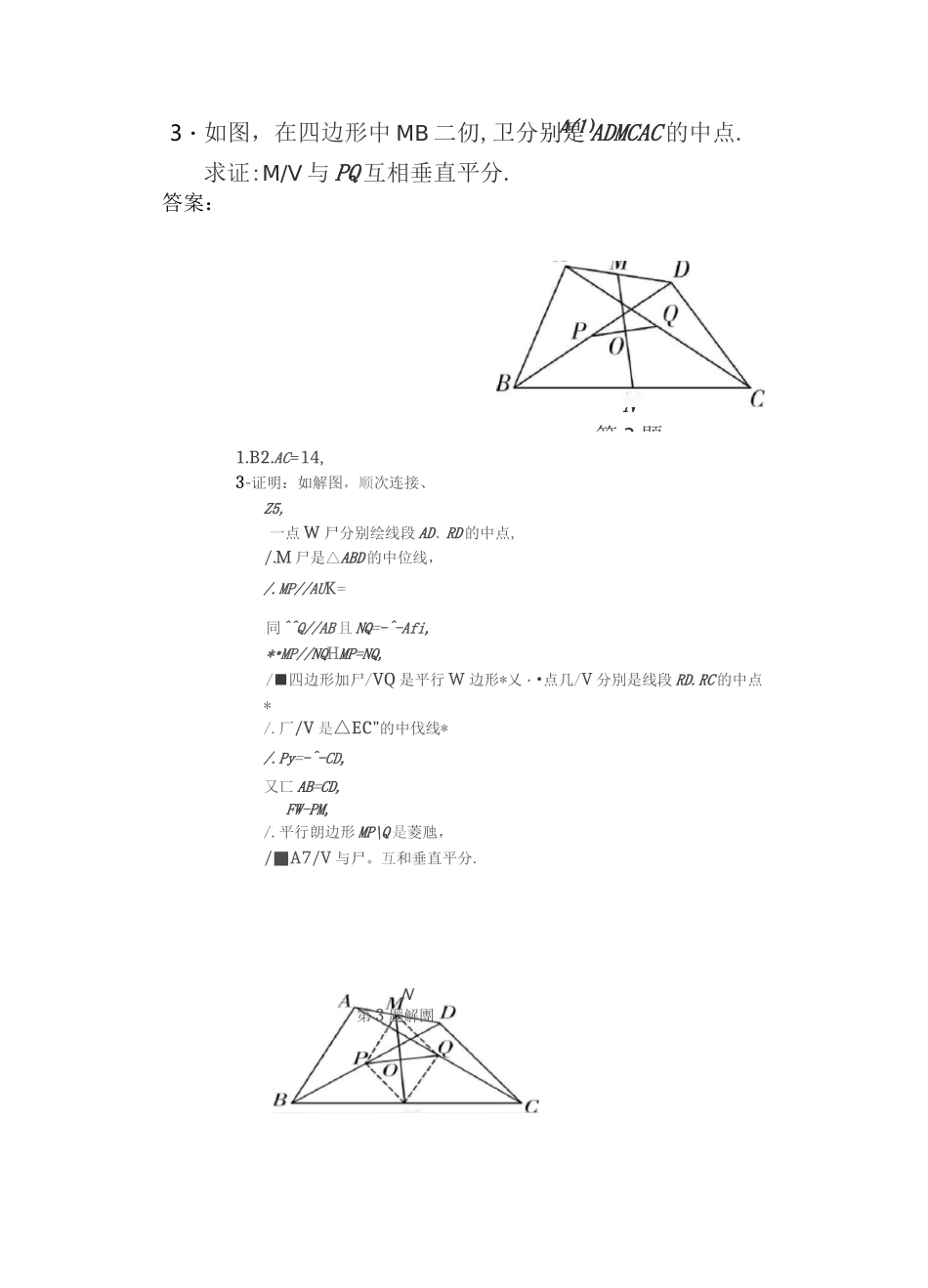
D.20°初中几何“中点问题”七大模型多个中点出现或平行+中点(中点在平行线上)时,常考虑或构造三角形中位线1模型分析I在三角形中■如果有中点•可构造三角形的中位线,利用三角形中位线的性质定理:DE//BC.且DE=-△皿,解决线段之间的相等或比例关系及平行问题.AAD/\E连接处\EX\\RCBC练一练练练1-4ll®,在口仙仞中,对角线AC与RD相交于点O,E是边CD的中点,连接OE,若ABC=60°,ABAC=*0化则zi的度数为乩50°C.30°第1题图2.如图应是△佔C的边BC的中点/TV平分上丄4N于点N,且旳£二呂,M/V=3•求4C的长”第2题图N第3题3・如图,在四边形中MB二仞,卫分别是ADMCAC的中点.求证:M/V与PQ互相垂直平分.答案:1.B2.AC=14,3-证明:如解图,顺次连接、Z5,一点W尸分别绘线段AD、RD的中点,/.M尸是△ABD的中位线,/.MP//AUK=同^^Q//AB且NQ=-^-Afi,*•MP//NQHMP=NQ,/■四边形加尸/VQ是平行W边形*乂・•点几/V分別是线段RD.RC的中点*/.厂/V是△EC"的中伐线*/.Py=-^-CD,又匸AB=CD,FW-PM,/.平行朗边形MP\Q是菱虺,/A7/V■与尸。互和垂直平分.N第3题解團A⑴直角三角形中遇到斜边上的中点,常联想“斜边上DBBC的中线等于斜边的一半”八构造直角三角形U斜边上的中线的中线,利用肆斜边上的中线等于斜边的一半“可得CD^AD^BD^~AB来解题,有吋有直角无中点,要找中点,可简记为“直角+中点,等腰必呈现:此模型作用:①证明线段相等或求线段长;②构造角相等进行等量代换.直角三角形中有斜边中点时*常作斜边上1模型分析练一练%;ADR第4题图4.如图^ACB=9()\D为M的中点,连接DC并延长到E,使CE=yCD.H点B作BF//DE,与AE的延长线交于点F,若前二&求=4*的长度.4,AB=6.5.证明:•••仞丄DB点E为屈的中点,DE=BE=yAB,LABD=LBDE.TDE//BC,LCBD^LBDE,厶ABD=MD,旳平分AABC.老型三等腰三角形中遇到底边上的中点,常联想“三线合•”的性质扌旻nIcL1模型分析|等腰三角形中有底边上的中点时,常作底边的中线,利用等腰三角形底边中线、高线、顶角平分“三线合一^的性质得至\\:ABAD=ZCAD,AD丄込ED二CD.解决线段相等及平行问题、角度之间的相等问题.AA练一AENBRDC第6题图6.如图.AABC中川Z?二M,点D是M的中点上是卫C上一点,且AE二AD*若乙第7题求MEDC的度数7.女II图「在△/!/?C^(SAS),人=90°,人AF丄BF.910B第9题图ABDC第10题图.如图,在周长为20的平行四边形肚仞中.AB^AD.AC.BD相交于点OWE丄加交AD于点E,连接RE.求仏A肚的周长.•如图,/\AI3C中fAD是高,CE是中线*点f;是(:E的中点,必丄C伙点(;为匝足+求证:DCBE.模型四遇到三角形一边垂线过这边中点时,可以考虑用垂直平分线的性质1模型分析I当三角形一边垂线过这边中点时级可以考虑用垂直平分线的性质得到辭二唇证明线段间的数量关系-答案:DEBEDCBEAEG2AB9.AABE的周长为10.10.证明:如解图,连接D&,vG是CE的中点J)G1CE,二DG是CE的垂直平分线,二DE—DC、vAABC中/D是髙,他是中线,二DE是RtA/lPZ?的斜边AB上的屮线,B1)C第10题解图模型五中线等分三角形面积11-在ZUBC中点D,E,F分别为&C9AD,CE的中点,12.如图,在边长为。的正方形ABCD中丄是AE的中点,D&交AC于点F,则△CDF的面积为()第11题图且S△砂=16,则S^OEFA.2B.8A.—a1B.—a2C.—aI),—a4323答案:cBD务S(因为/VlBD与ZUCD是两个等底同高的三角形)1模型分析14D是厶ABC的中线,则S酗叽心练一练练练模型六圆中弦(或弧)的中点,考虑垂径定理及圆周角定(点E是弦AB的中点)(点C是的中点)1模型分析」〈1)圆心。是直径的中点,常与已知中点连接、或过点0作一边的平行线或垂直构造中位线解题;(2)圆中遇到弦的中点,联想“垂径定理=岀现“四中...