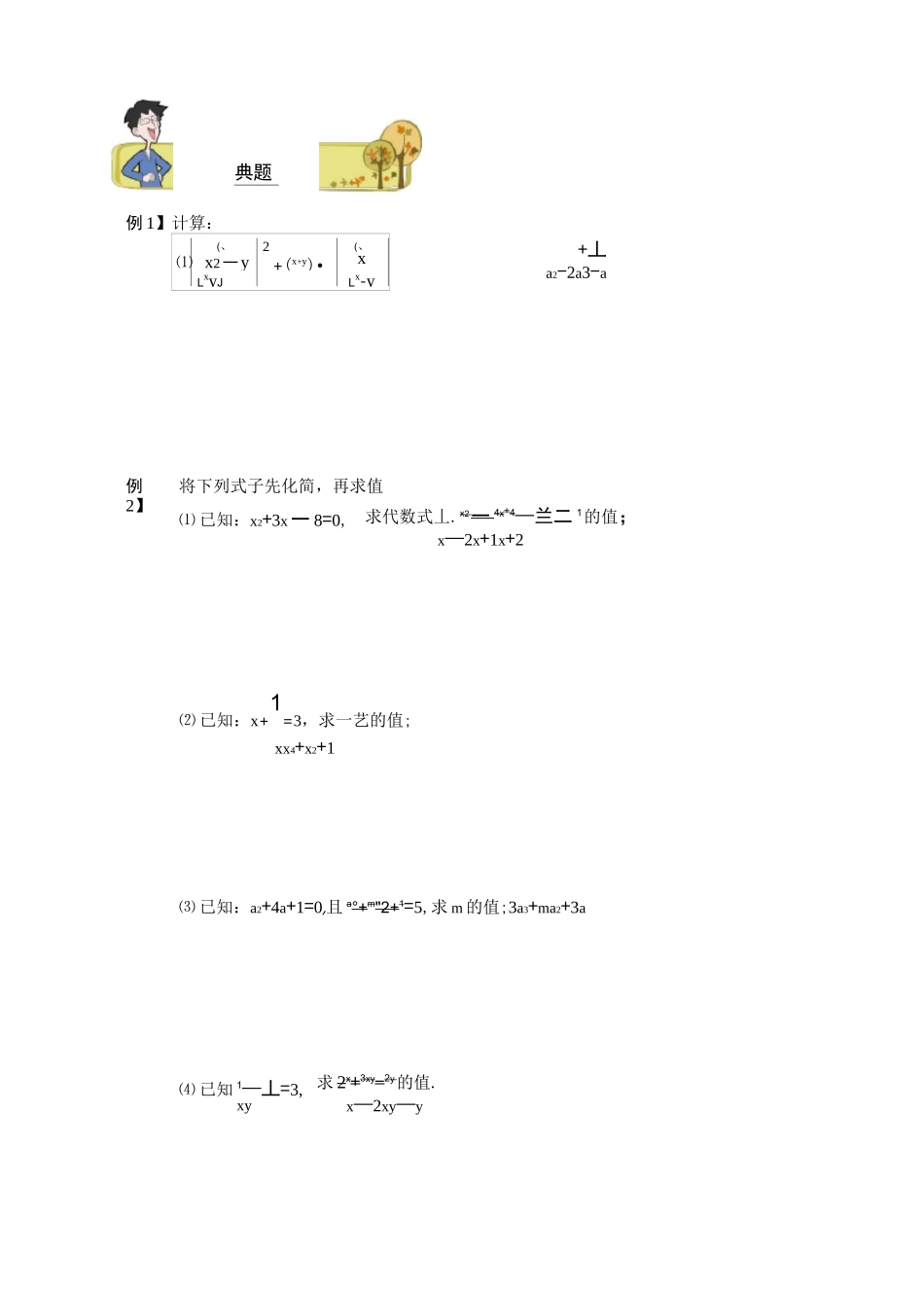
x2例题精讲(x+y22【引例】计算—-——、一—x—y3x丿【解析】原式J—3xx+y3xx+y-(x+y)分式恒等变形W分式的混合运笄与化简求值分式恒等变形分式的恒等变形部分分式与分离常数22x+y2:—-+(x+y3xx+y3xx+y2x知识互联*思路导题型一:分式的混合运算与化简求值于—对于分式的混合运算和化简求值来说,最为重要的就是细心运算,不要跳步.个别的题目要注意是否有简便方法.典题精练例1】计算:例2】⑴(、x2一y2+(x+y)•(、xLxyJLx-y将下列式子先化简,再求值⑴已知:x2+3x一8=0,+丄a2-2a3-a求代数式丄.x2一4x+4—兰二1的值;x—2x+1x+2⑵已知:x+1=3,求一艺的值;xx4+x2+1⑶已知:a2+4a+1=0,且a°+m"2+1=5,求m的值;3a3+ma2+3a⑷已知1—丄=3,xy求2x+3xy-2y的值.x—2xy—y-(a+b)abca+b+c11111=aba+b+cca+bc—a—b—cabc(a+b+c)c(a+b+c)ac+bc+c2=一abab+ac+bc+c2=0..a(b+c)+c(b+c)=0(a+c)(b+c)=0a+c=0或b+c=0②当a+b=0时,即a=—b综上所述c=—a,或a=—b,或b=—c.恒等概念是对两个代数式而言,如果两个代数式里的字母换成任意的数值,这两个代数式的值都相等,就说这两个代数式恒等.表示两个代数式恒等的等式叫做恒等式.将一个代数式换成另一个和它恒等的代数式,叫做恒等变形(或恒等变换).以恒等变形的意义来看,它不过是将一个代数式从一种形式变为另一种形式,但有一个条件要求变形前和变形后的两个代数式是恒等的,就是“形”变“值”不变.1111【解析】1+1+1=1一则丄=ab—1c(a+b+c)【例4】若求证:【例3】若n为自然数,且1+-+-=-一abca+b+ca+b+c=1ab+a+1bc+b+1ca+c+1ab(a+b)x-2(a-b)4x+==—典题精求证:1111++=a2n+1b2n+1C2n+1a2n+1b2n+1C2n+1解x+2x-2x2-4x2-4所以,解得{b=24典题精【例5】已知严-子+2=3+-A+-B,其中A、B为常数,求4A-2B的值.\x—1)\x+1丿x—1x+1【例6】⑴若整数m使为正整数,则m的值为.1+m⑵若x取整数,则使分式6X+3的值为整数的x的值有()•2x-1A.3个B.4个C.6个D.8个突破i【例7】已知亠二丄二丄=k,求k的值.b+ca+ca+b⑵已知分式耳尹的值为零’那么X的值是⑶当Xx—1时,分式X2+5的值为正⑷当x满足时,x±j<0.训练2.⑴(、X2—y22-(x—y)-(、XLxyJLx-y训练3.已知x--=3,求一x2的值.xX4+X2+1a2—5a+2a2—4a2+4a+4,其中训练4.已知22:x=△+-B^_C,其中A、B、C为常数,求A+B+C的值.X2lx—1丿XX2X一1题型一分式的混合运算与化简求值巩固练习练习1】计算:【练习2】若x+y=_4,xy=_3,则式子+的值为.x+1y+1题型二分式的恒等变形巩固练习【练习3】已知x、y、z为三个不相等的实数,且x+-=y+1=z+1,求证:x2y2z2=1.yzx2题型三部分分式与分离常数巩固练习【练习4】若———二土8恒成立,求M、N的值.x+2x—2x2—4【练习5】当x为何值时,分式彳有最小值?最小值是多少?2X2+x+1