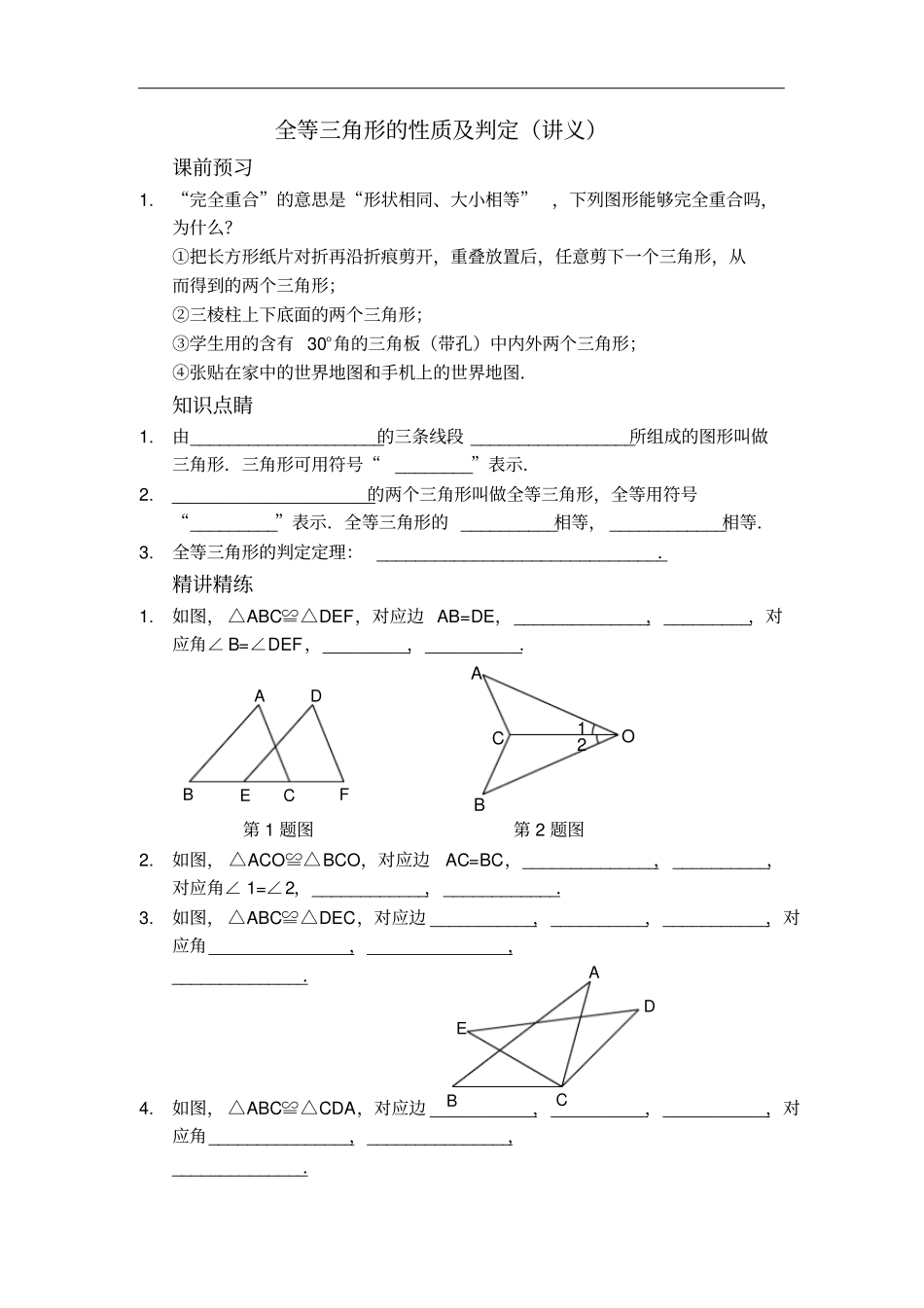
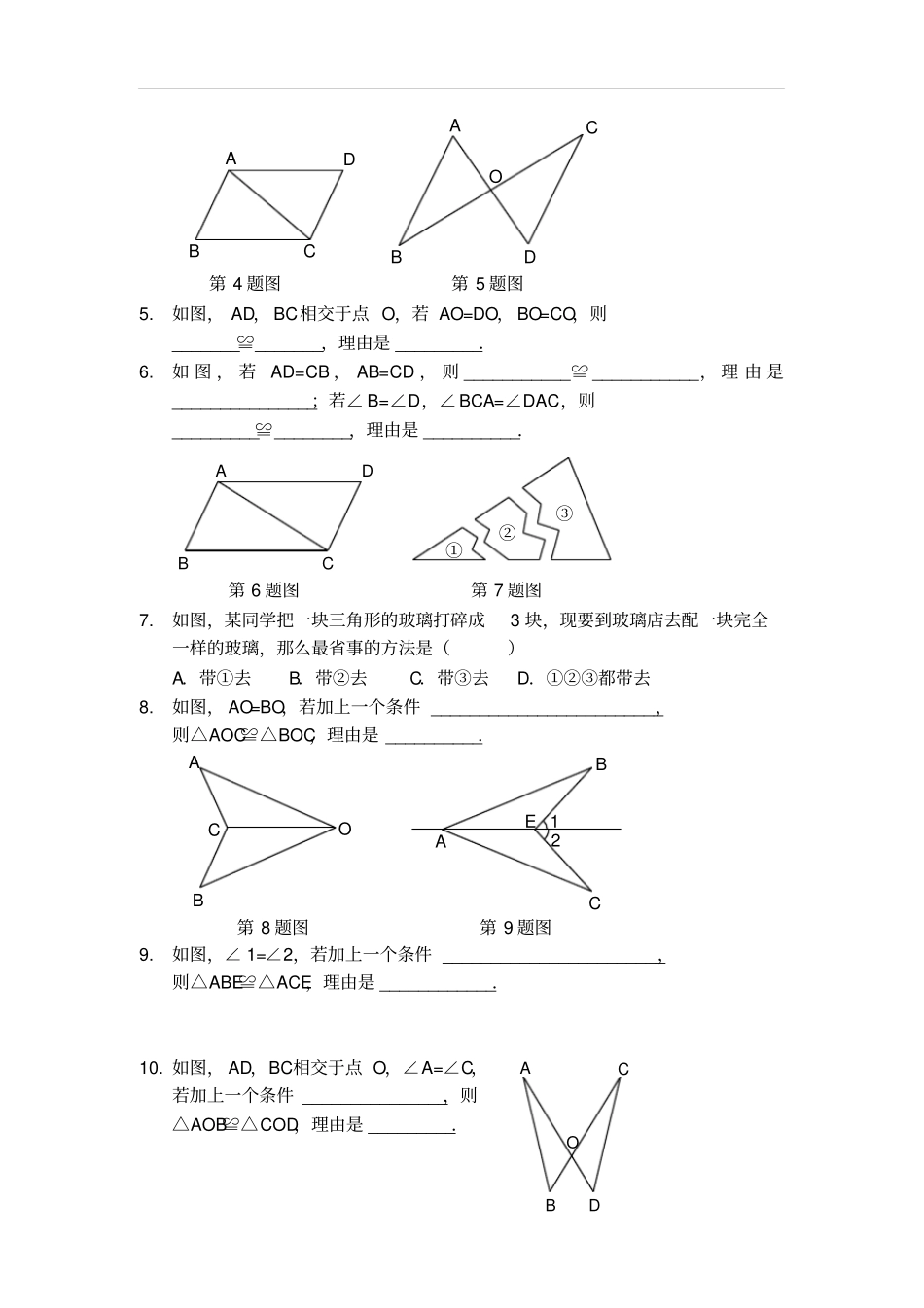
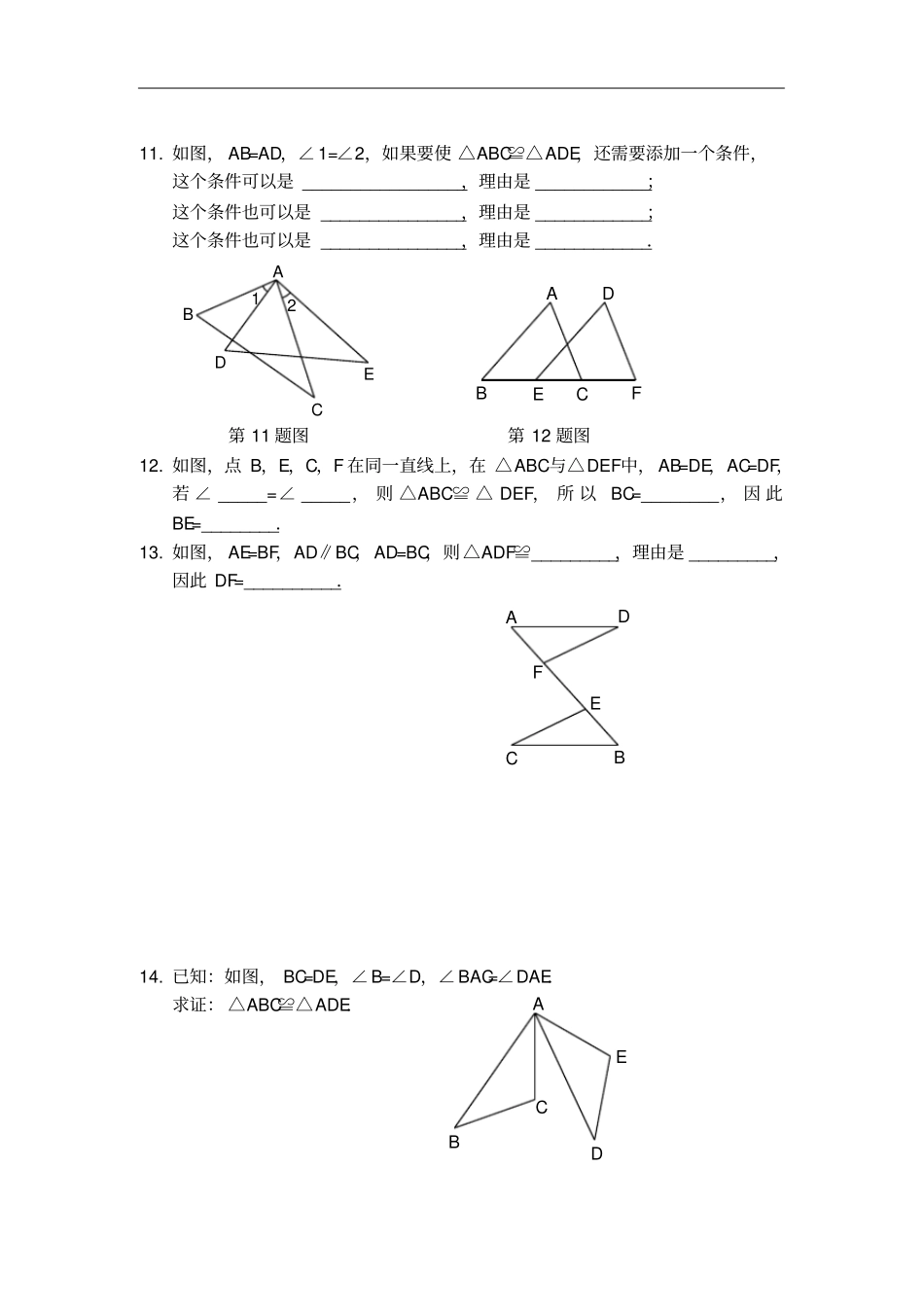
全等三角形的性质及判定(讲义)课前预习1.“完全重合”的意思是“形状相同、大小相等”,下列图形能够完全重合吗,为什么?①把长方形纸片对折再沿折痕剪开,重叠放置后,任意剪下一个三角形,从而得到的两个三角形;②三棱柱上下底面的两个三角形;③学生用的含有30°角的三角板(带孔)中内外两个三角形;④张贴在家中的世界地图和手机上的世界地图.知识点睛1.由____________________的三条线段_________________所组成的图形叫做三角形.三角形可用符号“________”表示.2._____________________的两个三角形叫做全等三角形,全等用符号“_________”表示.全等三角形的__________相等,____________相等.3.全等三角形的判定定理:______________________________.精讲精练1.如图,△ABC≌△DEF,对应边AB=DE,______________,_________,对应角∠B=∠DEF,_________,__________.FEDCBAACB12O第1题图第2题图2.如图,△ACO≌△BCO,对应边AC=BC,______________,__________,对应角∠1=∠2,____________,____________.3.如图,△ABC≌△DEC,对应边___________,__________,___________,对应角_______________,_______________,______________.4.如图,△ABC≌△CDA,对应边___________,__________,___________,对应角_______________,_______________,______________.EDCBADCBAODCBA第4题图第5题图5.如图,AD,BC相交于点O,若AO=DO,BO=CO,则_______≌_______,理由是_________.6.如图,若AD=CB,AB=CD,则___________≌___________,理由是_______________;若∠B=∠D,∠BCA=∠DAC,则_________≌________,理由是__________.ABCD③②①第6题图第7题图7.如图,某同学把一块三角形的玻璃打碎成3块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()A.带①去B.带②去C.带③去D.①②③都带去8.如图,AO=BO,若加上一个条件________________________,则△AOC≌△BOC,理由是__________.OBCA21ECBA第8题图第9题图9.如图,∠1=∠2,若加上一个条件_______________________,则△ABE≌△ACE,理由是____________.10.如图,AD,BC相交于点O,∠A=∠C,若加上一个条件_______________,则△AOB≌△COD,理由是_________.ODCBA11.如图,AB=AD,∠1=∠2,如果要使△ABC≌△ADE,还需要添加一个条件,这个条件可以是_________________,理由是____________;这个条件也可以是_______________,理由是____________;这个条件也可以是_______________,理由是____________.21ECDBAABCDEF第11题图第12题图12.如图,点B,E,C,F在同一直线上,在△ABC与△DEF中,AB=DE,AC=DF,若∠_____=∠_____,则△ABC≌△DEF,所以BC=________,因此BE=________.13.如图,AE=BF,AD∥BC,AD=BC,则△ADF≌_________,理由是_________,因此DF=__________.FEDCBA14.已知:如图,BC=DE,∠B=∠D,∠BAC=∠DAE.求证:△ABC≌△ADE.EDCBA15.已知:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:△ADC≌△AEB.16.已知:如图,AB=CD,AB∥CD.求证:△ABD≌△CDB.DCBAEDCBA【参考答案】课前预习1.①能②能③不能;大小不相等④不能;大小不相等知识点睛1.不在同一直线上,首尾顺次相接,△2.能够完全重合,≌,对应边,对应角3.SAS,SSS,ASA,AAS精讲精练1.AC=DF,BC=EF,∠A=∠D,∠ACB=∠F2.AO=BO,CO=CO,∠A=∠B,∠ACO=∠BCO3.AB=DE,AC=DC,BC=EC∠A=∠D,∠B=∠E,∠ACB=∠DCE4.AB=CD,AC=CA,BC=DA∠B=∠D,∠BAC=∠DCA,∠BCA=∠DAC5.△AOB,△DOC,SAS6.△ABC,△CDA,SSS;△ABC,△CDA,AAS7.C8.AC=BC,SSS(答案不唯一)9.BE=CE,SAS(答案不唯一)10.AB=CD,AAS(答案不唯一)11.AC=AE,SAS;∠B=∠D,ASA;∠C=∠E,AAS12.A,D,EF,CF13.△BCE,SAS,CE14.证明:如图,在△ABC和△ADE中BACDAEBDBCDE(已知)(已知)(已知)∴△ABC≌△ADE(AAS)15.证明:如图,在△ADC和△AEB中AAACABCB(公共角)(已知)(已知)∴△ADC≌△AEB(ASA)16.解:如图,DCBA21∵AB∥CD∴∠1=∠2在△ABD和△CDB中12ABCDBDDB(已知)(已证)(公共边)∴△ABD≌△CDB(SAS)