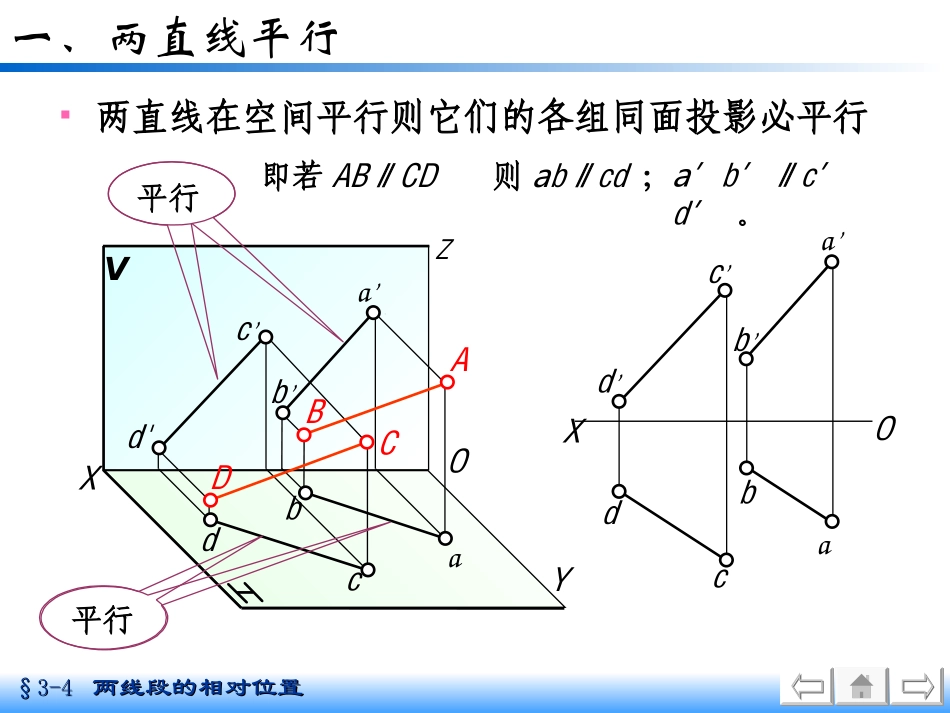
§3-4§3-4两线段的相对位置两线段的相对位置§3-4两直线的相对位置§3-4两直线的相对位置一、两直线平行一、两直线平行二、两直线相交二、两直线相交三、两直线交叉三、两直线交叉§3-4§3-4两线段的相对位置两线段的相对位置VXZYO一、两直线平行两直线在空间平行则它们的各组同面投影必平行a’b’c’d'abcdACBD平行OXabb’a’c’d’dc平行即若AB∥CD则ab∥cd;a’b’∥c’d’。§3-4§3-4两线段的相对位置两线段的相对位置一、两直线平行例1过点E(e、e’)作直线∥AB。OXee’a’b’ba若使EF∥AB,须ef∥ab;e’f’∥a’b’。ff’分析:作图:解题完毕§3-4§3-4两线段的相对位置两线段的相对位置VXZY二、两直线相交空间两直线相交,其同面投影必相交,且交点的投影符合点的投影规律。BCa'bab'OADdd'c'ck'kKOXabb’a’c’d’dckk'§3-4§3-4两线段的相对位置两线段的相对位置VXZY三、两直线交叉DACBc'd'b'a'badcⅣⅠⅡⅢ(2’)1‘3(4)既不平行也不相交的空间两直线称为交叉。投影图上的交点是重影点。OXabb’a’c’d’dc(2’)1‘3(4)4’3’12不符合投影规律O§3-4§3-4两线段的相对位置两线段的相对位置判断两直线的相对位置例1判断AB、EF两直线的相对位置。相交OXabb’a’f’e’efk’k’b’a’分析:判断方法:方法一作第三投影(略)方法二按定比性。k由于a’k’:k’b’=ak:kb结论:所以AB、EF相交。解题完毕§3-4§3-4两线段的相对位置两线段的相对位置判断两直线的相对位置例2判断AB、CD两直线的相对位置。交叉OXabb’a’c’d’dc分析:判断方法:方法一作第三投影(略)方法二按定比性。(略)方法三:假定AB、CD平行,则ABCD共面,AD和BC必相交,AB、CD两交叉直线。结论:平行?交叉?作图:§3-4§3-4两线段的相对位置两线段的相对位置本节结束