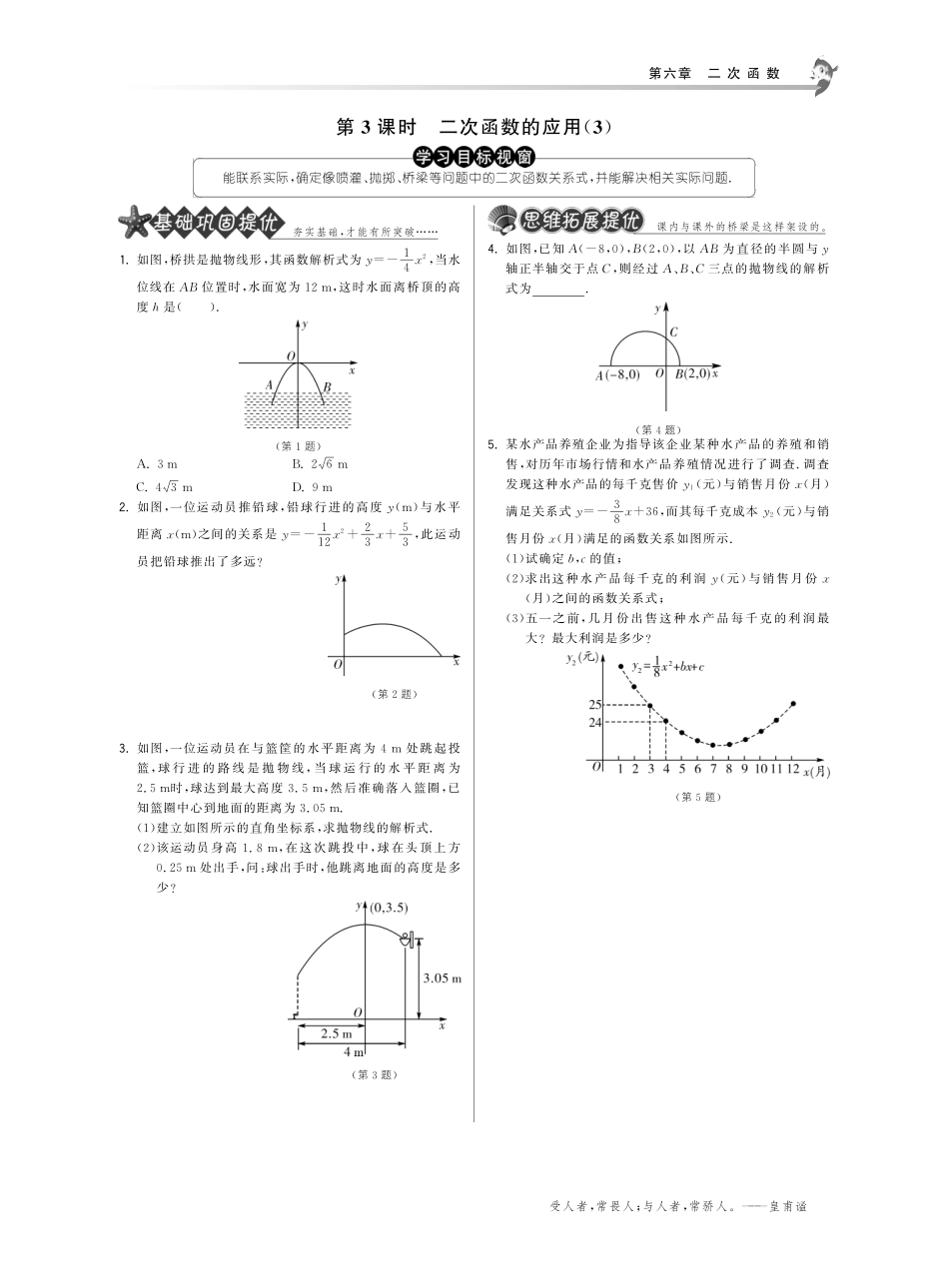
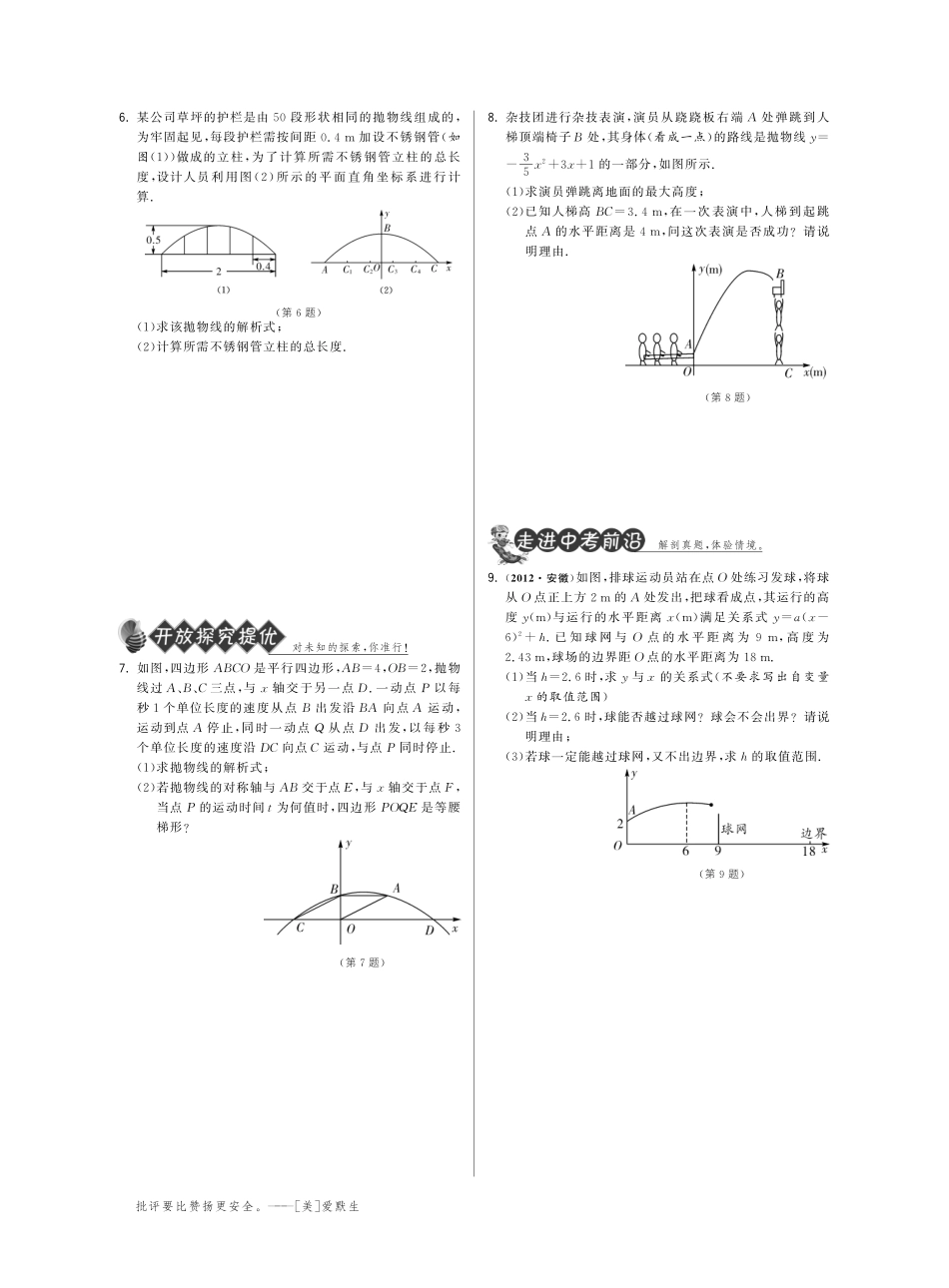
第六章二次函数受人者,常畏人;与人者,常骄人.———皇甫谧第3课时二次函数的应用(3)能联系实际,确定像喷灌、抛掷、桥梁等问题中的二次函数关系式,并能解决相关实际问题.夯实基础,才能有所突破1.如图,桥拱是抛物线形,其函数解析式为y=-14x2,当水位线在AB位置时,水面宽为12m,这时水面离桥顶的高度h是().(第1题)A.3mB.26mC.43mD.9m2.如图,一位运动员推铅球,铅球行进的高度y(m)与水平距离x(m)之间的关系是y=-112x2+23x+53,此运动员把铅球推出了多远?(第2题)3.如图,一位运动员在与篮筐的水平距离为4m处跳起投篮,球行进的路线是抛物线,当球运行的水平距离为2.5m时,球达到最大高度3.5m,然后准确落入篮圈,已知篮圈中心到地面的距离为3.05m.(1)建立如图所示的直角坐标系,求抛物线的解析式.(2)该运动员身高1.8m,在这次跳投中,球在头顶上方0.25m处出手,问:球出手时,他跳离地面的高度是多少?(第3题)课内与课外的桥梁是这样架设的.4.如图,已知A(-8,0),B(2,0),以AB为直径的半圆与y轴正半轴交于点C,则经过A、B、C三点的抛物线的解析式为.(第4题)5.某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价y1(元)与销售月份x(月)满足关系式y=-38x+36,而其每千克成本y2(元)与销售月份x(月)满足的函数关系如图所示.(1)试确定b,c的值;(2)求出这种水产品每千克的利润y(元)与销售月份x(月)之间的函数关系式;(3)五一之前,几月份出售这种水产品每千克的利润最大?最大利润是多少?(第5题)批评要比赞扬更安全.———[美]爱默生6.某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图(1))做成的立柱,为了计算所需不锈钢管立柱的总长度,设计人员利用图(2)所示的平面直角坐标系进行计算.(第6题)(1)求该抛物线的解析式;(2)计算所需不锈钢管立柱的总长度.对未知的探索,你准行!7.如图,四边形ABCO是平行四边形,AB=4,OB=2,抛物线过A、B、C三点,与x轴交于另一点D.一动点P以每秒1个单位长度的速度从点B出发沿BA向点A运动,运动到点A停止,同时一动点Q从点D出发,以每秒3个单位长度的速度沿DC向点C运动,与点P同时停止.(1)求抛物线的解析式;(2)若抛物线的对称轴与AB交于点E,与x轴交于点F,当点P的运动时间t为何值时,四边形POQE是等腰梯形?(第7题)8.杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-35x2+3x+1的一部分,如图所示.(1)求演员弹跳离地面的最大高度;(2)已知人梯高BC=3.4m,在一次表演中,人梯到起跳点A的水平距离是4m,问这次表演是否成功?请说明理由.(第8题)解剖真题,体验情境.9.(2012安徽)如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h的取值范围.(第9题)第3课时二次函数的应用(3)1.D2.铅球落在x轴上,则y=0.因此,-112x2+23x+53=0.解得x1=10,x2=-2(不合题意,舍去).所以此运动员把铅球推出了10m.3.(1)由题意,知抛物线顶点坐标为(0,3.5)且抛物线过点(1.5,3.05).设y=a(x-0)2+3.5,即y=ax2+3.5.将(1.5,3.05)代入上式,得3.05=2.25a+3.5,a=-15,故y=-15x2+3.5.(2)当x=-2.5时,y=-0.2×(-2.5)2+3.5=2.25,他跳离地面的高度是2.25-1.8-0.25=0.20(m).4.y=-14(x+8)(x-2)5.(1)由题意,得25=18×32+3b+c,24=18×42+4b+c,{解得b=-178,c=2912.{(2)y=...