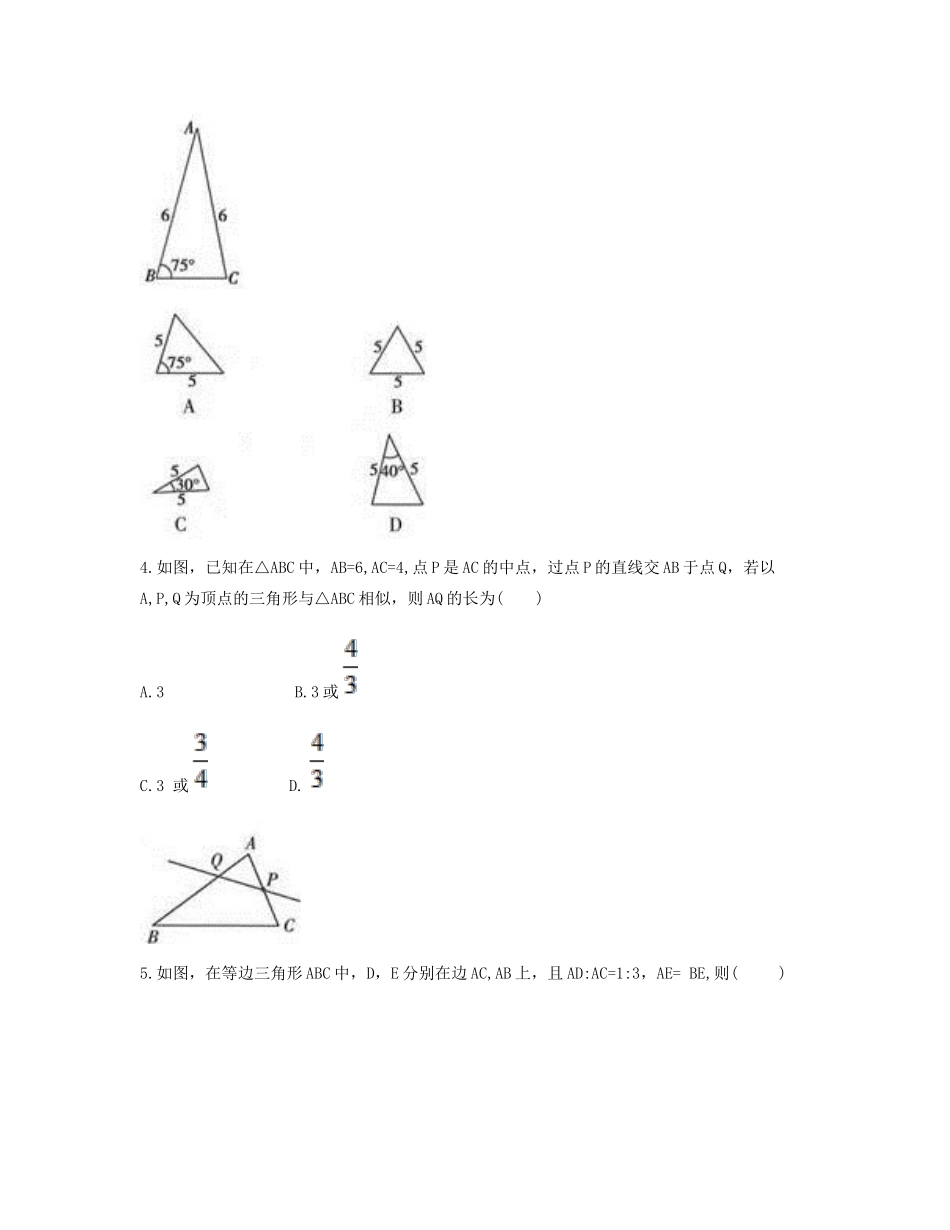
《利用两边和夹角判定三角形相似定理》A卷一、单项选择题(共5题,共45分)1.下列能判定△ABC∽△DEF的条件是()A.B.,∠A=∠FC.,∠B=∠ED.,∠A=∠D2.如图,四边形ABCD的对角线AC,BD相交于点O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是()A.①和②相似B.①和③相似C.①和④相似D.③和④相似3.如图,下列四个三角形中,与△ABC相似的是()4.如图,已知在△ABC中,AB=6,AC=4,点P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形与△ABC相似,则AQ的长为()A.3B.3或C.3或D.5.如图,在等边三角形ABC中,D,E分别在边AC,AB上,且AD:AC=1:3,AE=BE,则()A.△AED∽△BEDB.△AED∽△CBDC.△AED∽△ABDD.△BAD∽△BCD二、填空题(共1题,共10分)1.如图,在等边三角形ABC中,D为BC边上一点,E为AC边上一点,且AB=6,BD=2,当CE=________时,△ABD∽△DCE.三、解答题(共5题,共45分)1.如图,已知P为△ABC的中线AD上一点,且BD2=PD·AD.求证:△ADC∽△CDP.2.如图,已知在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=7,求AD的长.3.如图,已知在正方形ABCD中,Q为DC的中点,BP=3PC,求证:△CPQ∽△DQA.4.如图,在△ABC中,CD是边AB上的高,且.(1)求证:△ACD∽△CBD(2)求∠ACB的度数.5.如图,已知,∠DAC=40°.(1)求∠EAC的度数;(2)求证:△ABD∽△ACE.