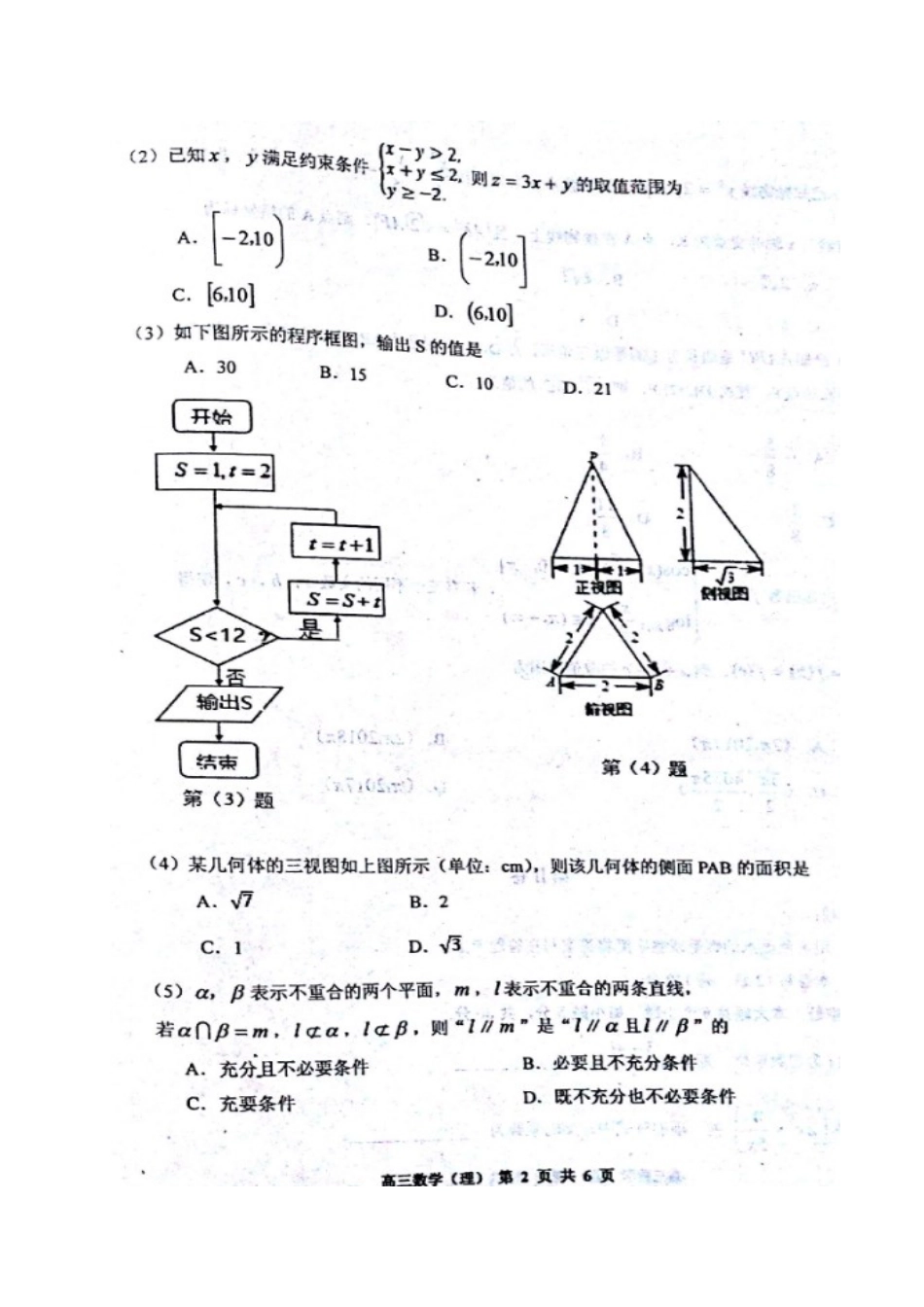
天津市红桥区2017届高三数学一模试题理(扫描版)高三数学(理)(1703)一、选择题(每小题5分,共40分)题号12345678答案CBBACDCB二、填空题(每小题5分,共30分)9.10.11.12.13.①②④⑤14.(0,4)三、解答题(本大题共6小题,共80分)(15)(本小题满分13分)(Ⅰ)......4所以的最小正周期.........................6由,得,所以的单调递减区间为,....................8(Ⅱ)由得故所以,因此,的最大为,最小值是..................................................13(16)(本小题满分13分)(Ⅰ)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡设事件为"采访该团3人中,恰有1人持金卡且持银卡者少于2人",事件为"采访该团人中,人持金卡,人持银卡",事件为"采访该团人中,人持金卡,人持银卡".由此可知所以在该团中随机采访人,恰有人持金卡且持银卡者少于人的概率是............6(Ⅱ)由题知的所有可能取值为,,,.............................7所以的分布列为所以..............11......................................................13(17)(本小题满分13分)(Ⅰ)设中点为G,连结,.ABCDEPyzx因为//,且,,所以//且,所以四边形为平行四边形.所以//,且.因为正方形,所以//,,所以//,且.所以四边形为平行四边形.所以//.因为平面,平面,所以//平面.……………………4(Ⅱ)如图建立空间坐标系,则,,,,,所以,,.设平面的一个法向量为,所以.令,则,所以.设与平面所成角为,ABCDEPyzxF则.所以与平面所成角的正弦值是.……………………8(Ⅲ)依题意,可设,则,.设平面的一个法向量为,则.令,则,所以.因为平面平面,所以,即,所以,点.所以.……………………13(18)(本小题满分13分)(Ⅰ)由已知①,②,①②得,即.又因为,所以.因为,所以,所以,所以,所以...............................................6(Ⅱ)由(Ⅰ)知所以设,则,两式相减得,整理得,所以.......................................13(19)(本小题满分14分)(Ⅰ)函数的定义域为..........................1...........................................................3令,得,其判别式.当,即时,,此时,在上单调递增.(2)当,即时,方程的两根为,.若,则,则时,,时,.此时,在上单调递减,在上单调递增.若,则,则时,,时,,时,.此时,上单调递增,在上单调递减,在上单调递增.综上所述,当时,函数在(0,)上单调递减,在上单调递增;当时,函数在(0,)上单调递增,在(,)上单调递减,在上单调递增;当时,函数上单调递增.........................................................7(Ⅱ)①由(Ⅰ)可知,函数有两个极值点,,等价于方程在有两不等实根,故...........................................9②证明:(Ⅰ)得,,且,.令,则.由于,则,故在上单调递减.故.所以所以................................................14(20)(本小题满分14分)(Ⅰ)由已知,所以,因为点在椭圆上,所以,解得,.所以所求椭圆方程为...............................................4(Ⅱ)设,,因为的垂直平分线过点,所以的斜率存在.当直线的斜率时,所以,,所以,当且仅当时取"",所以时,,..........6当直线的斜率时,设.所以消去得,由得①所以,,所以,,所以的中点为,...........................................8由直线的垂直关系有,化简得②由①②得,所以,......................................10又到直线的距离为,,,所以时,.由,所以,解得.即时,.综上,...................................................14