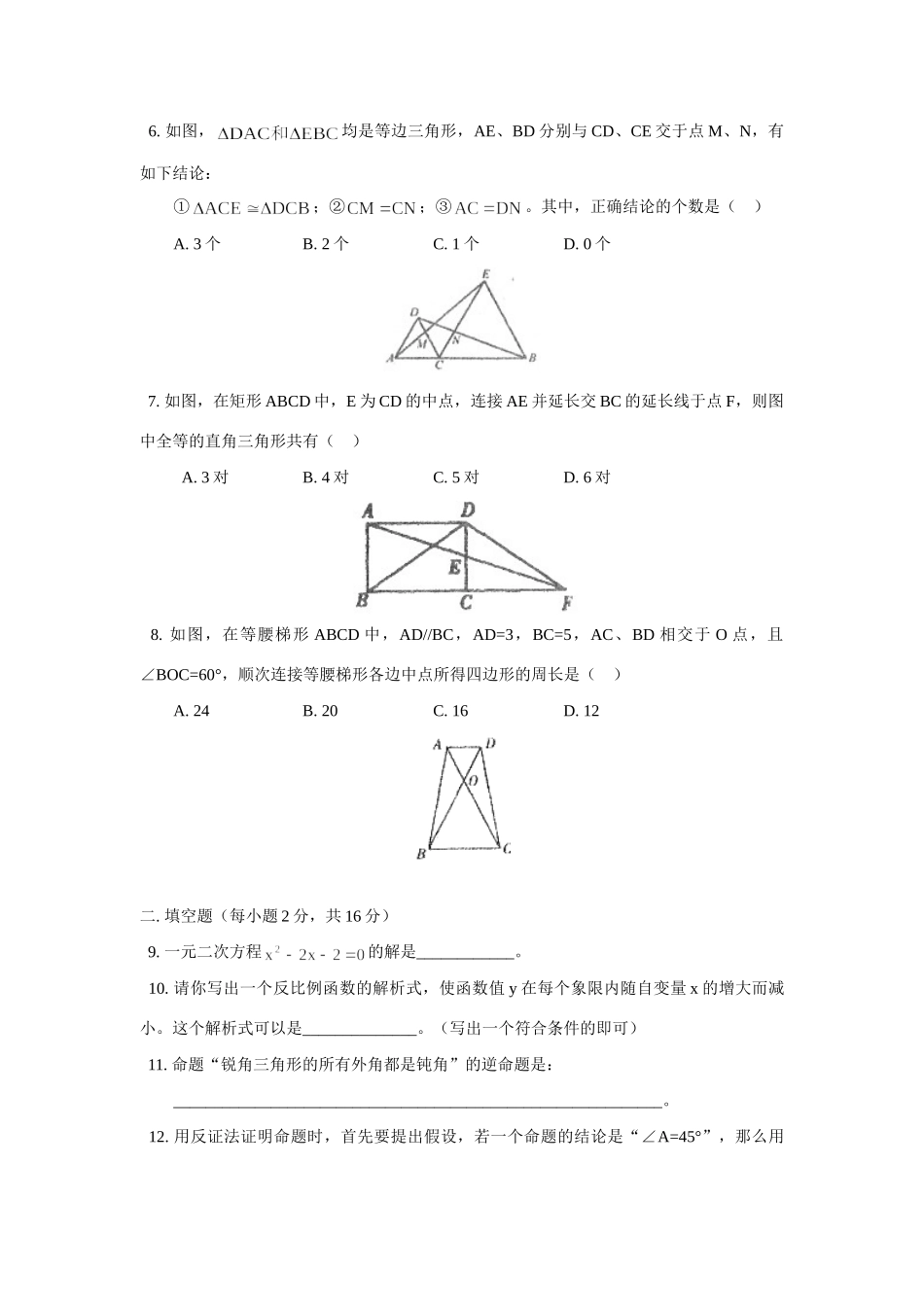
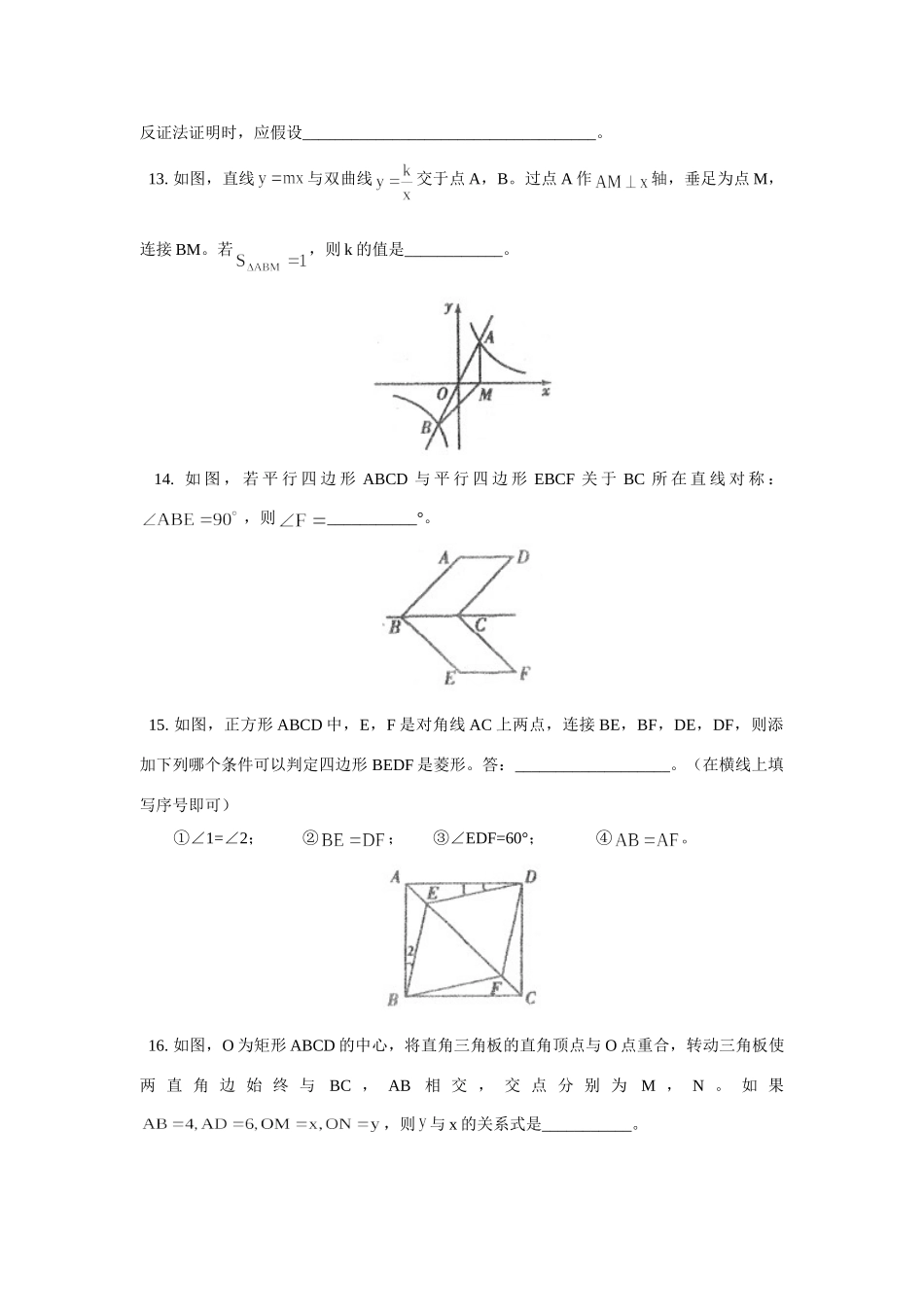
初三数学期中试卷北师大版【本讲教育信息】一.教学内容:期中试卷【模拟试题】(答卷可以使用计算器,考试时间90分钟,满分100分)一、选择题(每小题2分,共16分)1.一元二次方程的根是()A.B.C.D.2.一个三角形的两边长为8和6,第三边的边长是方程的根,则这个三角形的周长是()A.16B.16或18C.18D.243.已知反比例函数,则其图象在平面直角坐标系中可能是()4.已知点A(),,C(3,c)都在反比例函数的图象上,则a,b,c的大小关系为()A.B.C.D.5.如图,小芳和爸爸正在散步,爸爸身高1.8m,她在地面上的影长为2.1m。若小芳比爸爸矮0.3m,则她的影长为()A.1.3mB.1.65mC.1.75mD.1.8m6.如图,均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①;②;③。其中,正确结论的个数是()A.3个B.2个C.1个D.0个7.如图,在矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,则图中全等的直角三角形共有()A.3对B.4对C.5对D.6对8.如图,在等腰梯形ABCD中,AD//BC,AD=3,BC=5,AC、BD相交于O点,且∠BOC=60°,顺次连接等腰梯形各边中点所得四边形的周长是()A.24B.20C.16D.12二.填空题(每小题2分,共16分)9.一元二次方程的解是____________。10.请你写出一个反比例函数的解析式,使函数值y在每个象限内随自变量x的增大而减小。这个解析式可以是______________。(写出一个符合条件的即可)11.命题“锐角三角形的所有外角都是钝角”的逆命题是:____________________________________________________________。12.用反证法证明命题时,首先要提出假设,若一个命题的结论是“∠A=45°”,那么用反证法证明时,应假设____________________________________。13.如图,直线与双曲线交于点A,B。过点A作轴,垂足为点M,连接BM。若,则k的值是____________。14.如图,若平行四边形ABCD与平行四边形EBCF关于BC所在直线对称:,则___________°。15.如图,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪个条件可以判定四边形BEDF是菱形。答:___________________。(在横线上填写序号即可)①∠1=∠2;②;③∠EDF=60°;④。16.如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N。如果,则与x的关系式是___________。三.(每小题5分,共10分)17.用配方法解方程:18.如图,求作点P,使PA=PB,并使P点到∠MON的两边的距离相等。(保留作图痕迹,不必写出作法)四.(第19小题6分,第20小题8分,共14分)19.如图,BD为平行四边形ABCD的对角线,O为BD的中点,于点O,与AD、BC分别交于点E、F。求证:。20.如图,是等边三角形,过AC边上的点D作DG//BC,交AB于点G,在GD的延长线上取点E,使,连接AE、BD。(1)求证:;(2)过点E作EF//DB,交BC于点F,连接AF,求∠AFE的度数。五.(第21小题6分,第22小题8分,共14分)21.画出下面几何体的三种视图。22.商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件。据此规律,请回答:(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少元?(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?(提示:盈利=售价-进价)六.(本题满分8分)23.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律。如图,在同一时间,身高为1.6m的小明(AB)的影子BC长是3m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得。(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;(2)求路灯灯泡的垂直高度GH;(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点处时,其影子的长为;当小明继续走剩下路程的到处时,其影子的长为;当小明继续走剩下路程的到处时,……按此规律继续走下去,当小明走剩下路程的到处时,其影子的长为________________m。(直接用含n的代数式表示)七.(本题满分10分)24.已知正...