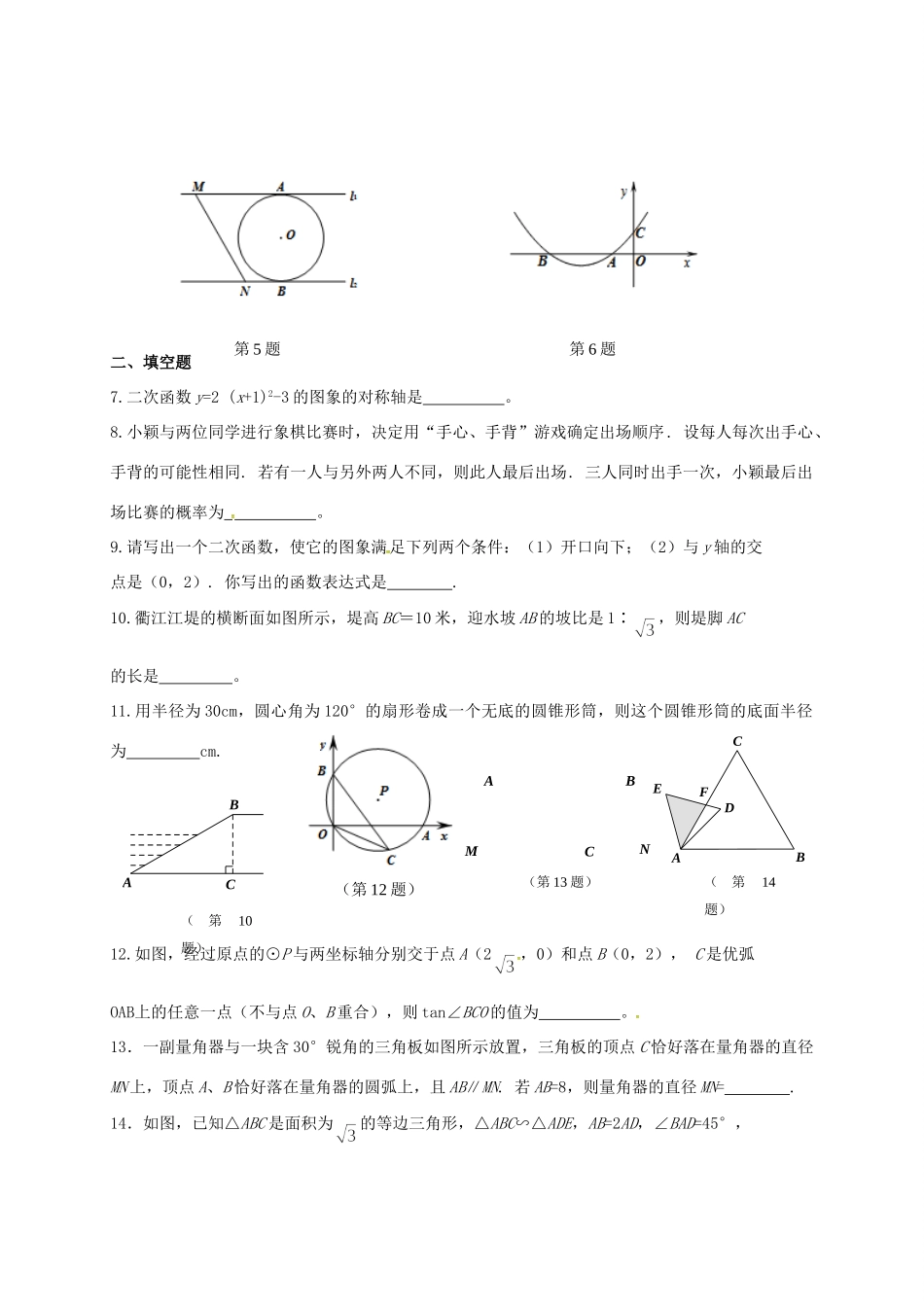
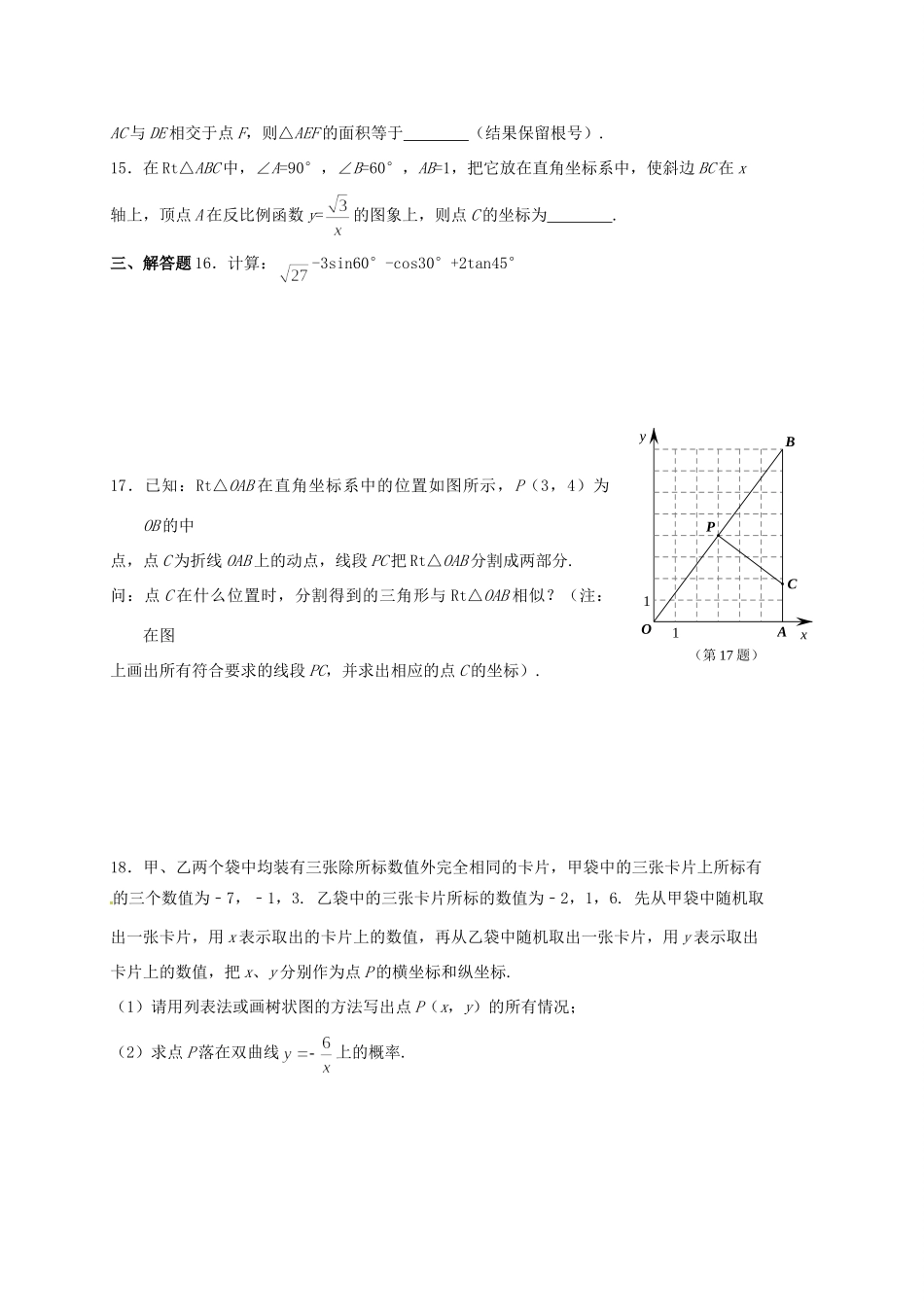
a第二次对折第一次对折b(第4题)(第3题)新港城中学九年级数学双休日作业(3.14-3.15)一、选择题1.反比例函数的图象经过点(-1,2),则这个函数的图象位于()A.第一、二象限B.第三、四象限C.第一、三象限D.第二、四象限2.已知,则代数式的值为()A.B.C.D.3.如右图的空心钢管的主视图画法正确的是()A.B.C.D.4.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是()A.a=bB.a=2bC.a=2bD.a=4b5.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.若⊙O的半径为1,∠AMN=60°,则下列结论不正确的是()A.MN=B.当MN与⊙O相切时,AM=C.l1和l2的距离为2D.当∠MON=90°时,MN与⊙O相切6.如图,抛物线y=ax2+bx+c与x轴的负半轴交于点A,B(点A在点B的右边),与y轴的正半轴交于点C,且OA=OC=1,则下列关系中正确的是()A.a+b=1B.b<2aC.a-b=-1D.ac<0NMCBA(第13题)FEDCBA(第14题)二、填空题7.二次函数y=2(x+1)2-3的图象的对称轴是。8.小颖与两位同学进行象棋比赛时,决定用“手心、手背”游戏确定出场顺序.设每人每次出手心、手背的可能性相同.若有一人与另外两人不同,则此人最后出场.三人同时出手一次,小颖最后出场比赛的概率为。9.请写出一个二次函数,使它的图象满足下列两个条件:(1)开口向下;(2)与y轴的交点是(0,2).你写出的函数表达式是.10.衢江江堤的横断面如图所示,堤高BC=10米,迎水坡AB的坡比是1∶,则堤脚AC的长是。11.用半径为30cm,圆心角为120°的扇形卷成一个无底的圆锥形筒,则这个圆锥形筒的底面半径为cm.12.如图,经过原点的⊙P与两坐标轴分别交于点A(2,0)和点B(0,2),C是优弧OAB上的任意一点(不与点O、B重合),则tan∠BCO的值为。13.一副量角器与一块含30°锐角的三角板如图所示放置,三角板的顶点C恰好落在量角器的直径MN上,顶点A、B恰好落在量角器的圆弧上,且AB∥MN.若AB=8,则量角器的直径MN=.14.如图,已知△ABC是面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,CBA(第10题)第5题第6题(第12题)(第17题)11yxPCBAOAC与DE相交于点F,则△AEF的面积等于(结果保留根号).15.在Rt△ABC中,∠A=90°,∠B=60°,AB=1,把它放在直角坐标系中,使斜边BC在x轴上,顶点A在反比例函数y=的图象上,则点C的坐标为.三、解答题16.计算:-3sin60°-cos30°+2tan45°17.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.问:点C在什么位置时,分割得到的三角形与Rt△OAB相似?(注:在图上画出所有符合要求的线段PC,并求出相应的点C的坐标).18.甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点P的横坐标和纵坐标.(1)请用列表法或画树状图的方法写出点P(x,y)的所有情况;(2)求点P落在双曲线上的概率.PCBOA(第19题)EDCBA图(1)图(2)19.已知:如图,P是⊙O的直径AB延长线上的一点,点C在⊙O上,AC=PC,∠ACP=120°.(1)求证:CP是⊙O的切线;(2)若AB=4cm,求图中阴影部分的面积.20.为倡导健康出行,衢州市道路运输管理局自2013年11月25日起向市民提供一种公共自行车作为代步工具,如图(1)所示是一辆自行车的实物图.车架档AC与CD的长分别为45.0cm,60.0cm,且它们互相垂直,∠CAB=76°,AD∥BC,如图(2).(1)求车架档AD的长;(2)求车链横档AB的长.(结果精确到0.1cm.参考数据:sin76°≈0.97,cos76°≈0.24,tan76≈4.00)21.某区政府大力扶持大学生创业.李刚在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:(第22题)FEPDCBAy=-10x+500.(1)设李刚...