九年级数学上学期期中试卷(五四制)试卷VIP专享VIP免费

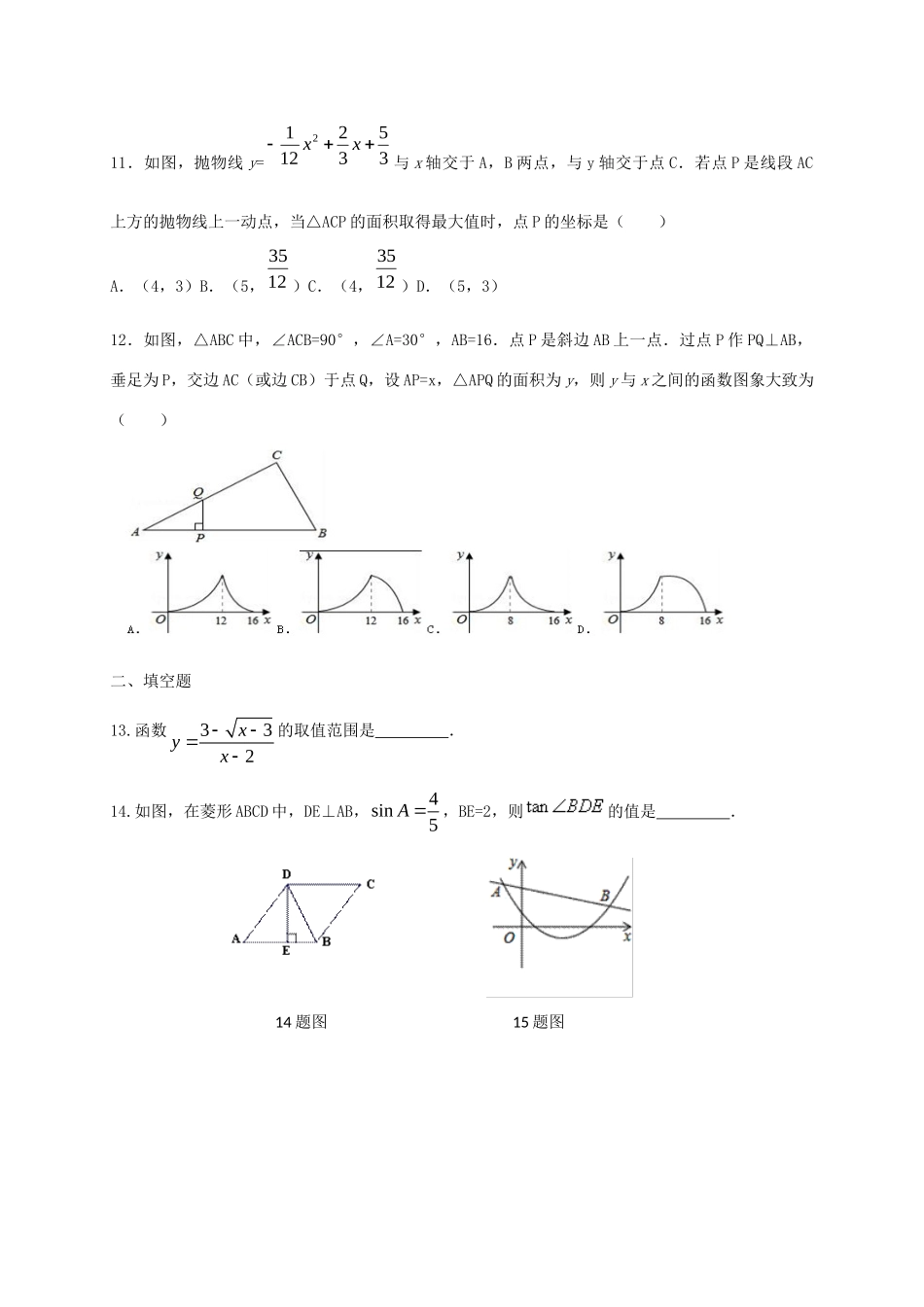
山东省威海经济技术开发区2017届九年级数学上学期期中试题一、选择题1．在Rt△ABC中，∠A=90°，如果把这个直角三角形的各边长都扩大2倍，那么所得到的直角三角形中，∠B的正切值（）A．扩大2倍B．缩小2倍C．扩大4倍D．大小不变2．把二次函数y=ax2+bx+c的图象向左平移4个单位或向右平移1个单位后都会经过原点，则二次函数图象的对称轴与x轴的交点是（）A．（﹣2.5，0）B．（2.5，0）C．（﹣1.5，0）D．（1.5，0）3．在△ABC中,若213sintan023AB,则∠C的度数为（）A．30°B．60°C．90°D．120°4．函数y＝ax－2(a≠0)与y＝ax2(a≠0)在同一平面直角坐标系中的图象可能是（）5．如图，△ABC中，AC﹦5，cosB=22，sinC=53，则△ABC的面积为（）A．221B．12C．14D．21第（5）题第（6）题第（7）题yyyA.B.C.D.xxxxy6．二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（）A．﹣3B．3C．﹣6D．97．已知抛物线y=ax2+bx+3在坐标系中的位置如上图所示，它与x，y轴的交点分别为A，B，P是其对称轴x=1上的动点，根据图中提供的信息，给出以下结论：①2a+b=0，②x=3是ax2+bx+3=0的一个根，③△PAB周长的最小值是+3．其中正确的是（）A．①②③B．仅有①②C．仅有①③D．仅有②③8．已知抛物线223yxx与x轴交于A、B两点，将这条抛物线的顶点记为C，连接AC、BC，则tan∠CAB的值为（）A．12B．55C．255D．29．若A（﹣，y1），B（，y2），C（，y3）为二次函数y=x2+4x+k的图象上的三点，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y1＜y3＜y210．轮船从B处以每小时25海里的速度沿南偏东30°方向匀速航行，在B处观测灯塔A位于南偏东75°方向上，轮船航行1小时到达C处，在C处观测灯塔A位于北偏东60°方向上，则C处于灯塔A的距离是（）海里．A．25B．25C．25D．50第（10）题第（11）题11．如图，抛物线y=35321212xx与x轴交于A，B两点，与y轴交于点C．若点P是线段AC上方的抛物线上一动点，当△ACP的面积取得最大值时，点P的坐标是（）A．（4，3）B．（5，1235）C．（4，1235）D．（5，3）12．如图，△ABC中，∠ACB=90°，∠A=30°，AB=16．点P是斜边AB上一点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（）二、填空题13.函数332xyx的取值范围是．14.如图，在菱形ABCD中，DE⊥AB，4sin5A，BE=2，则的值是．14题图15题图15.如图，已知二次函数2yaxbxc与一次函数ykxm的图像相交于点A（-3,5），B（7，2），则关于x的不等式2()0axbkxcm的解集是．．16.如图，在RT△BAD中，延长斜边BD到点C，使DC=12BD，连接AC，若tanB=，则tan∠CAD的值．17.平行于x轴的直线AC分别交抛物线21yx（x≥0）与223xy（x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则DEAB=．18.如图是二次函数y=a2x+bx+c（a≠0）图象的一部分，x=﹣1是对称轴，有下列判断：①b﹣2a=0；②4a﹣2b+c＜0；③a﹣b+c=﹣9a；④若（﹣3，1y），（32，2y）是抛物线上两点，则1y＞2y，其中正确的序号是．三、解答题19.（1）计算：222sin604cos30sin45tan60(cos60tan30)16题图17题图18题图（2）已知是锐角，且计算：101sin()(3.14)233tan22320.（8分）某小区为解决“停车难”问题，拟建造一个地下停车库．如图是该地下停车库坡道入口的设计示意图，其中水平线AB=10m，BD⊥AB，∠BAD=20°，点C在BD上，BC=1m．根据规定，地下停车库坡道入口上方要张贴限高标志，以提醒驾驶员所驾车辆能否安全驶入．李建认为CD的长度就是限制的高度，而孙杰认为应该以CE的长度作为限制的高度．李建和孙杰谁说的对？请你判断并计算出限制高度．（结果精确到0.1m，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）21.（8分）如图，小华站在河岸上的G点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船C的俯角是∠FDC=30°，若小华的眼睛与地面的距离是1.6米，BG=0.7米，BG平行于AC所在的...