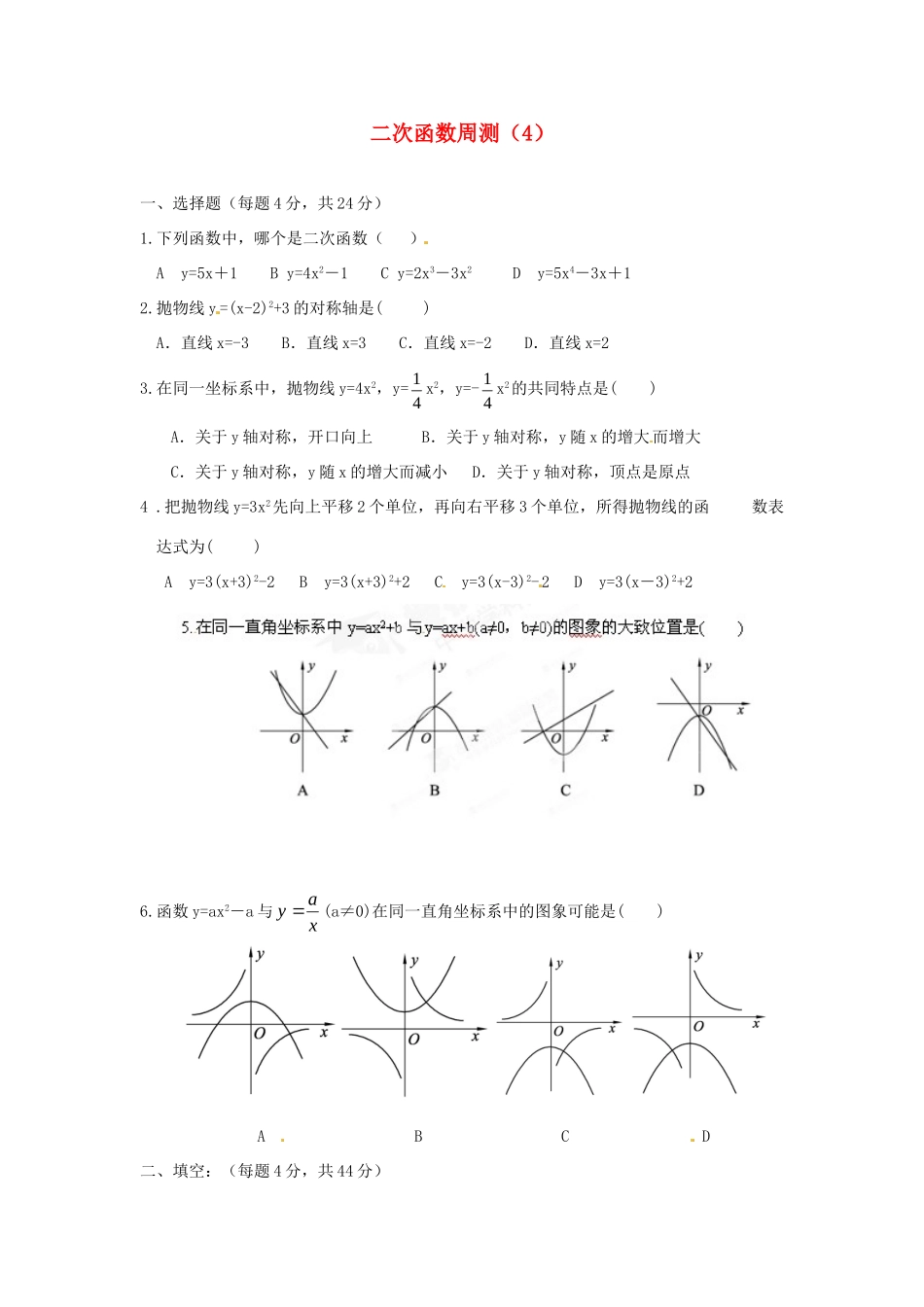
二次函数周测(4)一、选择题(每题4分,共24分)1.下列函数中,哪个是二次函数()Ay=5x+1By=4x2-1Cy=2x3-3x2Dy=5x4-3x+12.抛物线y=(x-2)2+3的对称轴是()A.直线x=-3B.直线x=3C.直线x=-2D.直线x=23.在同一坐标系中,抛物线y=4x2,y=14x2,y=-14x2的共同特点是()A.关于y轴对称,开口向上B.关于y轴对称,y随x的增大而增大C.关于y轴对称,y随x的增大而减小D.关于y轴对称,顶点是原点4.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得抛物线的函数表达式为()Ay=3(x+3)2-2By=3(x+3)2+2Cy=3(x-3)2-2Dy=3(x-3)2+26.函数y=ax2-a与xay(a≠0)在同一直角坐标系中的图象可能是()ABCD二、填空:(每题4分,共44分)7.已知抛物线的解析式为y=(x-2)2+1,则抛物线的顶点坐标是。8.二次函数y=3(x-1)2+2的最小值是。9.函数y=2(x+1)2是由y=2x2向_____平移_____个单位得到的.10.函数y=-3(x-1)2+1是由y=3x2向_____平移_____个单位,再向_____平移_____个单位得到的.11.函数y=3(x-2)2的对称轴是_____,顶点坐标是_____,图象开口向_____,当x_____时y随x的增大而减小,当x_______时,函数y有最_______值,是_______.12.函数y=-(x+5)2+7的对称轴是_______,顶点坐标是_______,图象开口向_______,当x_______时,y随x的增大而减小,当_______时,函数y有最_______值,是_______.13、二次函数y=ax2+4x+a的最大值是3,则a=_______.14、已知点P(5,25)在抛物线y=ax2上,则当x=1时,y的值为__________.15、函数y=x2+2x-8与x轴的交点坐标是_________.16.写出一个开口向上,顶点坐标是(2,-3)的函数解析式_______。17、已知一个直角三角形的两条直角边长的和是10cm。设这个直角三角形的面积为Scm2,其中一条直角边为xcm,求S关于x的函数关系式_________________________三、解答题18.通过配方,写出抛物线的开口方向、对称轴和顶点坐标。(5分4=20分)(1)y=x2+4x;(2)y=-x2+2x(3)y=-2x2+8x-6(4)y=x2-4x+319.把抛物线y=x2+bx+c向上平移2个单位,再向左平移4个单位,得到抛物线y=x2。(1)求b、c的值.(6分)(2)画出y=x2+bx+c的图像。(注意列表、描点、连线三个步骤。自己在下面的空白处建立坐标系)(6分)