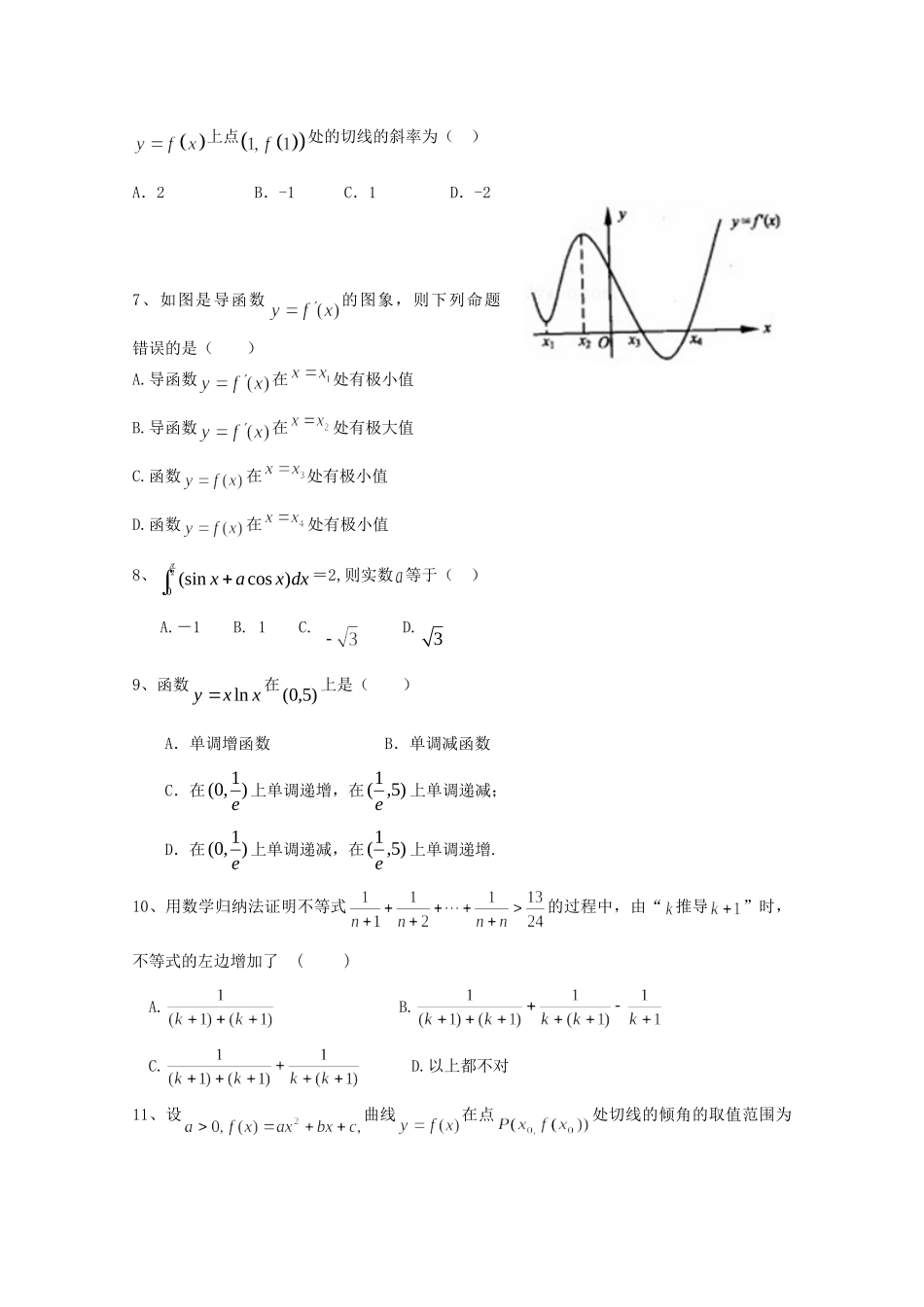
山东省青岛二中2012-2013学年高二数学下学期第三次模块(期中)试题理本试卷分第Ⅰ卷和第Ⅱ卷两部分.满分150分.考试用时120分钟.第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设,“”是“复数是纯虚数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分又不必要条件2、下面是关于复数的四个命题,其中的真命题为()的共轭复数为的虚部为A.B.C.D.3、因为指数函数是增函数(大前提),而是指数函数(小前提),所以是增函数(结论)上面推理的错误是()A.大前提错导致结论错B.小前提错导致结论错C.推理形式错导致结论错D.大前提和小前提错都导致结论错4、已知函数,则()A.B.C.D.5、若曲线处的切线分别为,且的值为()A.B.2C.D.6、设函数为可导函数,且满足关系式,则过曲线上点处的切线的斜率为()A.2B.-1C.1D.-27、如图是导函数的图象,则下列命题错误的是()A.导函数在处有极小值B.导函数在处有极大值C.函数在处有极小值D.函数在处有极小值8、20(sincos)xaxdx=2,则实数等于()A.-1B.1C.D.39、函数xxyln在)5,0(上是()A.单调增函数B.单调减函数C.在)1,0(e上单调递增,在)5,1(e上单调递减;D.在)1,0(e上单调递减,在)5,1(e上单调递增.10、用数学归纳法证明不等式的过程中,由“推导”时,不等式的左边增加了()A.B.C.D.以上都不对11、设曲线在点处切线的倾角的取值范围为,则P点到曲线对称轴距离的取值范围为()12、已知函数yfx是定义在实数集R上连续的奇函数,且当0,0xfxxfx(其中fx的导函数是fx),设1122log4log4,22,afbf,则的大小关系是()A.cabB.cbaC.abcD.第Ⅱ卷(共100分)二、填空题:本大题共4小题,每小题4分,共16分.13.若为复数,且,则z.14.由曲线围成区域面积为.15.德国数学家莱布尼兹发现了下面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前5行的规律,写出第6行第3个数是16.已知矩形的两个顶点位于轴上,另两个顶点位于抛物线在轴上方的曲线上,则矩形的面积最大为.三、解答题:本大题共6个小题,共74分.17.(本小题满分12分)(Ⅰ)已知zC,且i=z23iz(为虚数单位),求复数2iz的虚部.(Ⅱ)已知(为虚数单位),且为纯虚数,求实数的值.18.(本小题满分12分)已知函数(Ⅰ)若函数的图象在处的切线方程为,求的值;(Ⅱ)若函数在为增函数,求的取值范围.19.(本小题满分12分)已知是互不相等的非零实数,用反证法证明三个方程,,至少有一个方程有两个相异实根.20.(本小题满分12分)已知等差数列na和等比数列nb,.(I)求na、nb;(II)对于Nn,试比较na、nb的大小并用数学归纳法证明你的结论.21.(本小题满分12分)设函数.(Ⅰ)求函数)(xf的单调递增区间;(Ⅱ)若关于x的方程在区间内恰有两个相异的实根,求实数a的取值范围.22.(本小题满分14分)函数,其中.(Ⅰ)试讨论函数的单调性;(Ⅱ)已知当(其中是自然对数的底数)时,在上至少存在一点,使成立,求的取值范围;(Ⅲ)求证:当时,对任意,,有.附加题:(本小题满分10分)定义在R上的函数满足函数xaxxfln)(2在[1,2]上为增函数,xaxxg)(在(0,1)为减函数.(Ⅰ)求的解析式;(Ⅱ)当时,若212)(xbxxf在]1,0(x内恒成立,求的取值范围.