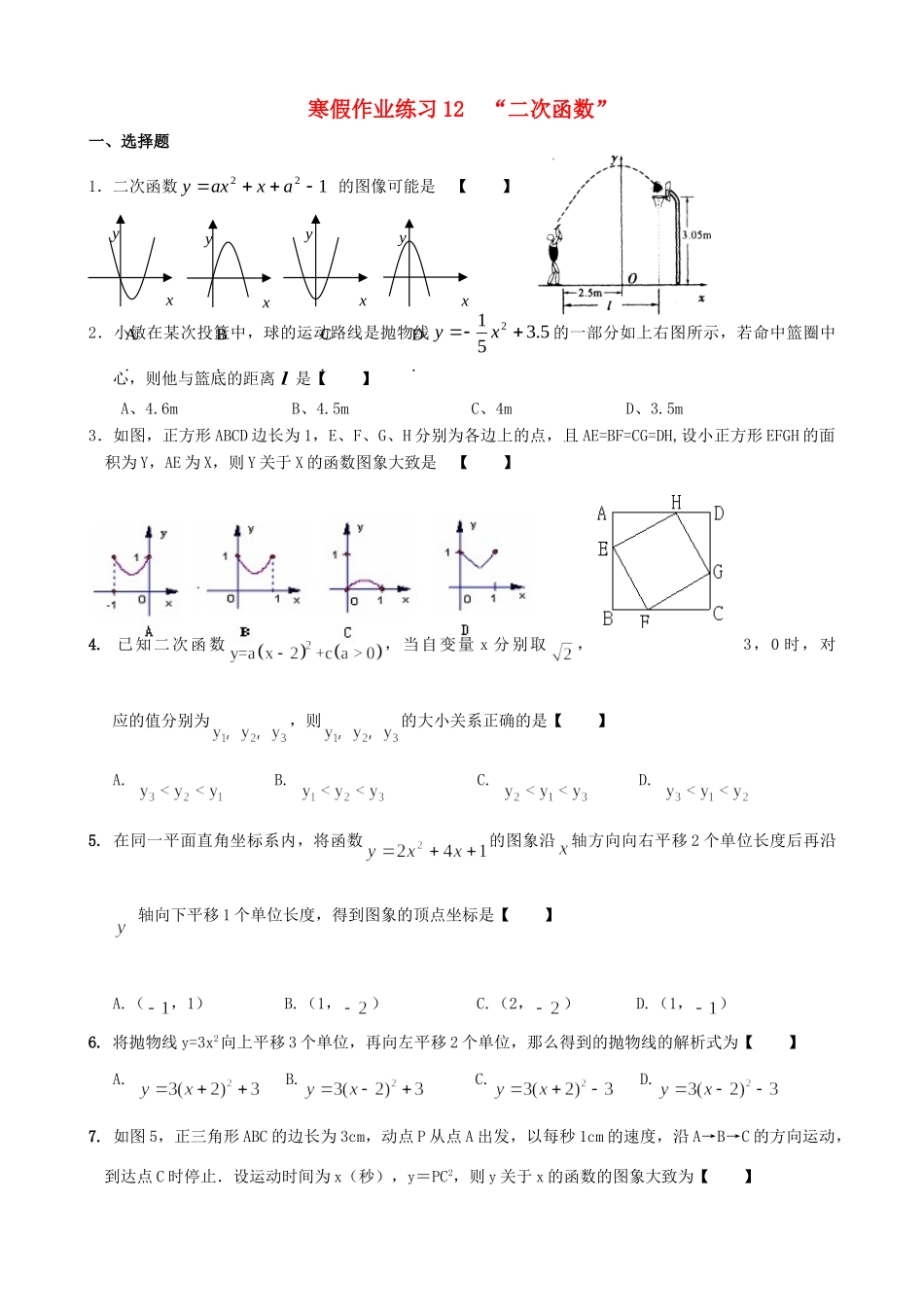
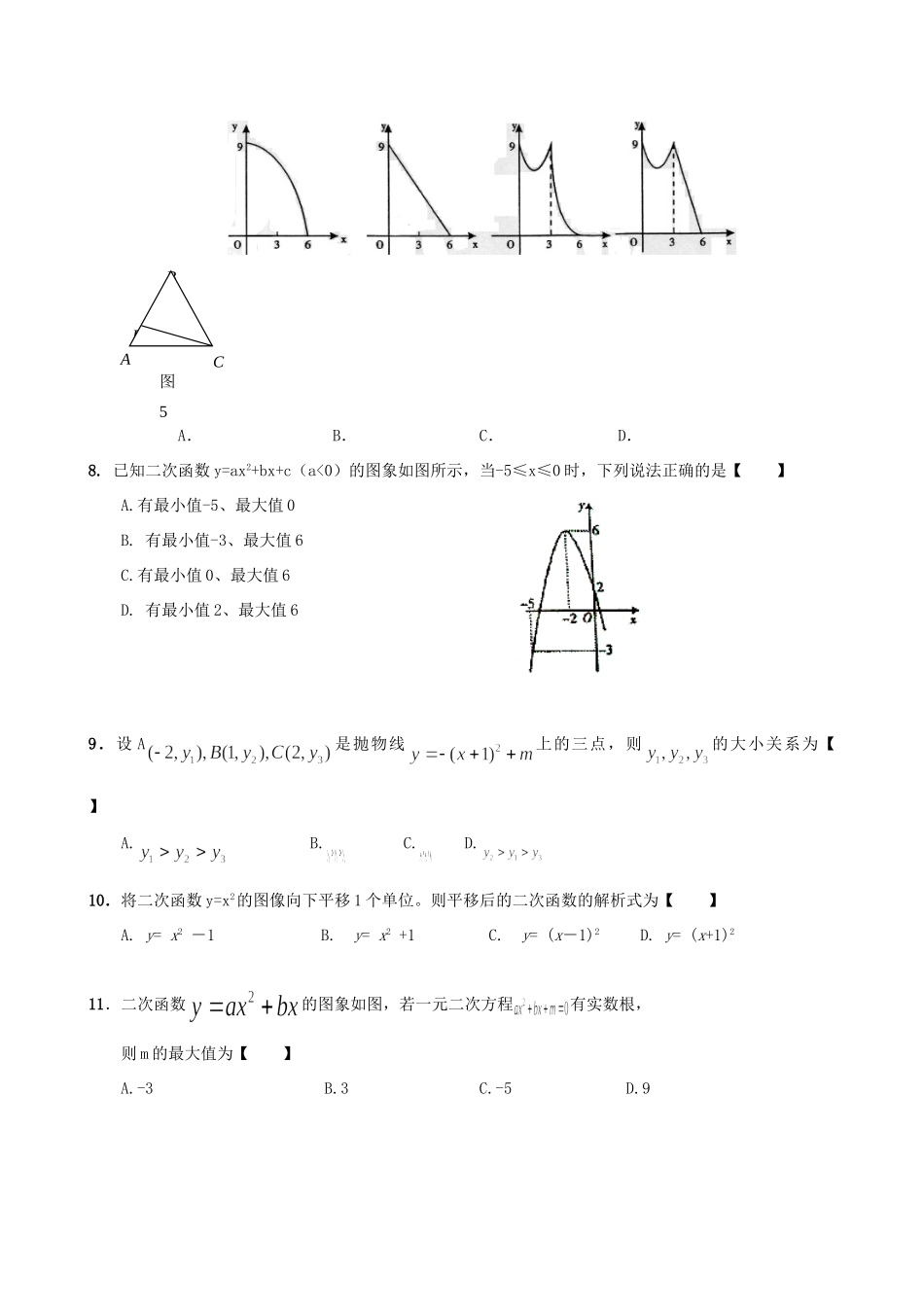
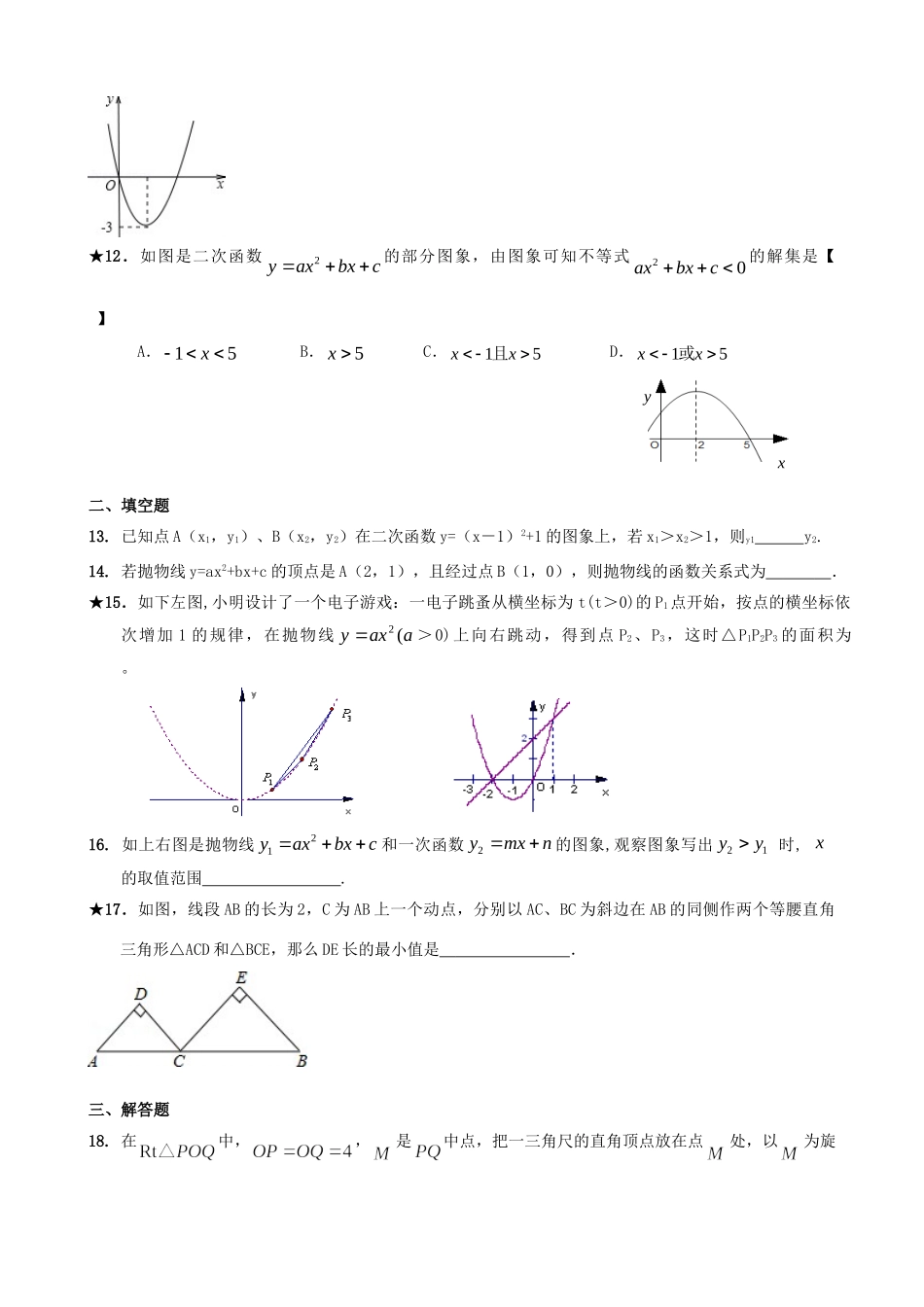
寒假作业练习12“二次函数”一、选择题1.二次函数122axaxy的图像可能是【】2.小敏在某次投篮中,球的运动路线是抛物线5.3512xy的一部分如上右图所示,若命中篮圈中心,则他与篮底的距离l是【】A、4.6mB、4.5mC、4mD、3.5m3.如图,正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为Y,AE为X,则Y关于X的函数图象大致是【】4.已知二次函数,当自变量x分别取,3,0时,对应的值分别为,则的大小关系正确的是【】A.B.C.D.5.在同一平面直角坐标系内,将函数的图象沿轴方向向右平移2个单位长度后再沿轴向下平移1个单位长度,得到图象的顶点坐标是【】A.(,1)B.(1,)C.(2,)D.(1,)6.将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为【】A.B.C.D.7.如图5,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致为【】A.xyB.xyC.xyD.xyA.B.C.D.8.已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,下列说法正确的是【】A.有最小值-5、最大值0B.有最小值-3、最大值6C.有最小值0、最大值6D.有最小值2、最大值69.设A是抛物线上的三点,则的大小关系为【】A.B.C.D.10.将二次函数y=x2的图像向下平移1个单位。则平移后的二次函数的解析式为【】A.y=x2-1B.y=x2+1C.y=(x-1)2D.y=(x+1)211.二次函数的图象如图,若一元二次方程有实数根,则m的最大值为【】A.-3B.3C.-5D.9ABCP图5★12.如图是二次函数2yaxbxc的部分图象,由图象可知不等式20axbxc的解集是【】A.15xB.5xC.15xx且D.15xx或二、填空题13.已知点A(x1,y1)、B(x2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1y2.14.若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为.★15.如下左图,小明设计了一个电子游戏:一电子跳蚤从横坐标为t(t>0)的P1点开始,按点的横坐标依次增加1的规律,在抛物线aaxy(2>0)上向右跳动,得到点P2、P3,这时△P1P2P3的面积为。16.如上右图是抛物线21yaxbxc和一次函数2ymxn的图象,观察图象写出21yy时,x的取值范围.★17.如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是.三、解答题18.在中,,是中点,把一三角尺的直角顶点放在点处,以为旋yx转中心,旋转三角尺,三角尺的两直角边与的两直角边分别交于点.(1)求证:;(2)连接,探究:在旋转三角尺的过程中,的周长是否存在最小值,若存在,求出最小值,若不存在.请说明理由.19.许多家庭以燃气作为烧水做饭的燃料,节约用气是我们日常生活中非常现实的问题。某款燃气灶旋钮位置从0度到90度(如图),燃气关闭时,燃气关闭时,燃气灶旋钮的位置为0度,旋钮角度越大,燃气流量越大,燃气开到最大时,旋钮角度为90度.为测试燃气灶旋钮在不同位置上的燃气用量,在相同条件下,选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时,其火力不能够将水烧开,故选择旋钮角度度的范围是),记录相关数据得到下表:旋钮角度(度)2050708090所用燃气量(升)73678397115(1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示所用燃气量y升与旋钮角度x度的变化规律?(2)当旋钮角为多少时,烧开一壶水所用燃气量最少?最少是多少?(3)某家庭使用此燃气灶,以前习惯把燃气开到最大,现采用最节省燃气的旋钮角度,每月平均能节约燃气10立方米,求该家庭以前每月的平均燃气用量.20.在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.(1)用含x的代数式表示△MNP的面积S;(2)当x为何值时,⊙O与直线BC相切?(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?ABCMND图2OABCMNP图1OABCMNP图3O