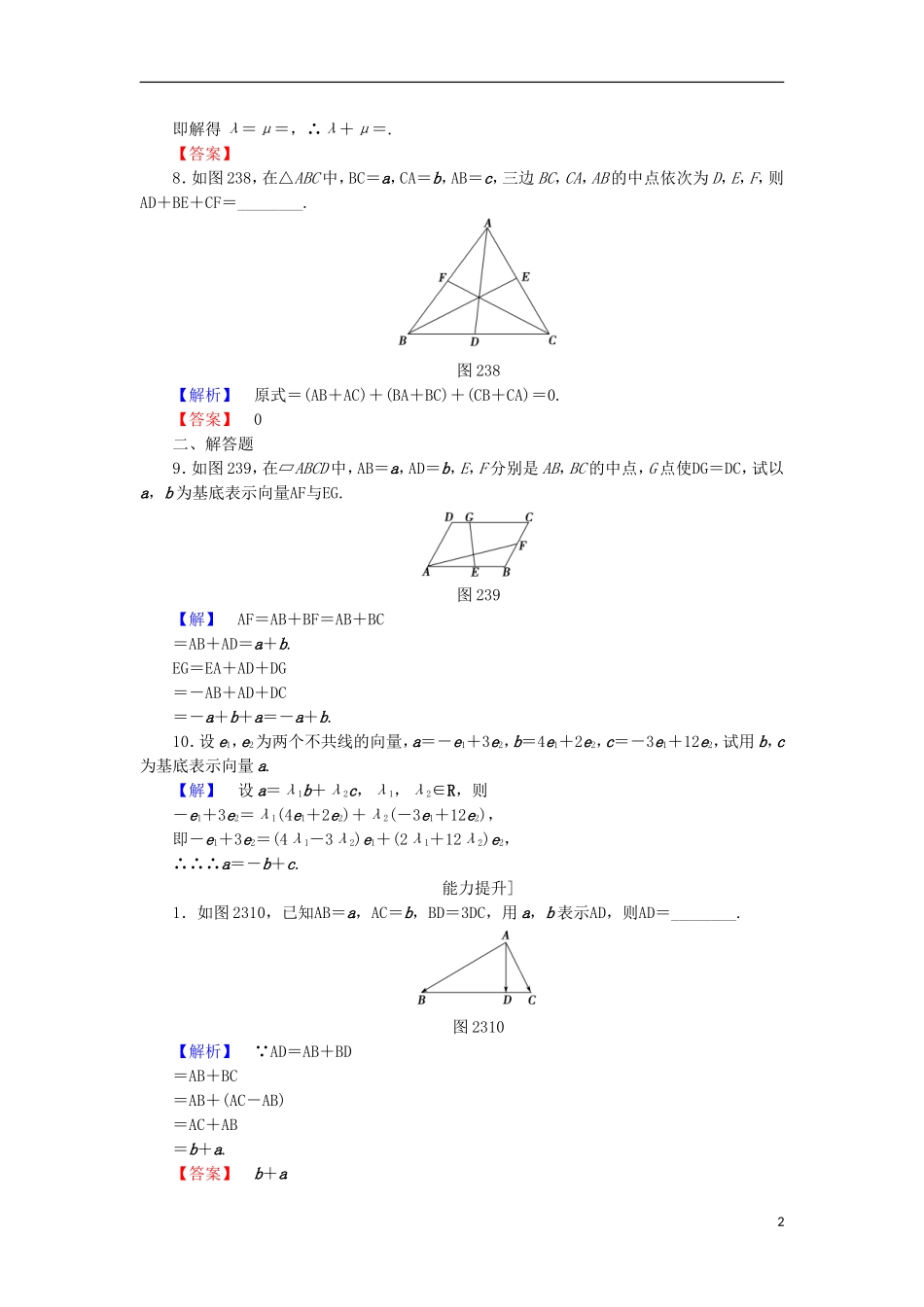
学业分层测评(十八)平面向量基本定理(建议用时:45分钟)学业达标]一、填空题1.设O是平行四边形ABCD的两条对角线AC与BD的交点,有下列向量组:①AD与AB;②DA与BC;③CA与DC;④OD与OB.其中可作为这个平行四边形所在平面内其他所有向量的基底的是________.【解析】如图所示,AD与AB为不共线向量,可以作为基底.CA与DC为不共线向量,可以作为基底.DA与BC,OD与OB均为共线向量,不能作为基底.【答案】①③2.已知向量a和b不共线,实线x,y满足向量等式(2x-y)a+4b=5a+(x-2y)b,则x+y的值等于________.【解析】由平面向量基本定理得解得∴x+y=1.【答案】13.(2016·苏州高一检测)在△ABC中,已知D是AB边上一点,若AD=2DB,CD=CA+λCB,则λ=________.【解析】∵AD=2DB,∴CD=CA+AD=CA+AB=CA+(CB-CA)=CA+CB.又∵CD=CA+λCB,∴λ=.【答案】4.若e1,e2是表示平面所有向量的一组基底,且a=3e1-4e2,b=6e1+ke2不能作为一组基底,则k的值为________.【解析】易知a∥b,故设3e1-4e2=λ(6e1+ke2),∴∴k=-8.【答案】-85.如图237所示,平面内的两条直线OP1和OP2将平面分割成四个部分Ⅰ,Ⅱ,Ⅲ,Ⅳ(不包括边界),若OP=aOP1+bOP2,且点P落在第Ⅰ部分,则a________0,b________0.(填“>”或“<”)图237【解析】由向量的分解可知,a<0,b>0.【答案】<>6.设e1,e2是不共线向量,e1+2e2与me1+ne2共线,则=________.【解析】由e1+2e2=λ(me1+ne2),得mλ=1且nλ=2,∴=2.【答案】27.(2016·南京高一检测)在平行四边形ABCD中,E和F分别是边CD和BC的中点,若AC=λAE+μAF,其中λ,μ∈R,则λ+μ=________.【导学号:06460053】【解析】设BC=b,BA=a,则AF=b-a,AE=b-a,AC=b-a,代入AC=λAE+μAF,得b-a=b-a,1即解得λ=μ=,∴λ+μ=.【答案】8.如图238,在△ABC中,BC=a,CA=b,AB=c,三边BC,CA,AB的中点依次为D,E,F,则AD+BE+CF=________.图238【解析】原式=(AB+AC)+(BA+BC)+(CB+CA)=0.【答案】0二、解答题9.如图239,在▱ABCD中,AB=a,AD=b,E,F分别是AB,BC的中点,G点使DG=DC,试以a,b为基底表示向量AF与EG.图239【解】AF=AB+BF=AB+BC=AB+AD=a+b.EG=EA+AD+DG=-AB+AD+DC=-a+b+a=-a+b.10.设e1,e2为两个不共线的向量,a=-e1+3e2,b=4e1+2e2,c=-3e1+12e2,试用b,c为基底表示向量a.【解】设a=λ1b+λ2c,λ1,λ2∈R,则-e1+3e2=λ1(4e1+2e2)+λ2(-3e1+12e2),即-e1+3e2=(4λ1-3λ2)e1+(2λ1+12λ2)e2,∴∴∴a=-b+c.能力提升]1.如图2310,已知AB=a,AC=b,BD=3DC,用a,b表示AD,则AD=________.图2310【解析】∵AD=AB+BD=AB+BC=AB+(AC-AB)=AC+AB=b+a.【答案】b+a22.如图2311,在△ABC中,AN=NC,P是BN上的一点,若AP=mAB+AC,则实数m的值为________.图2311【解析】设NP=λNB,NP=AP-AN=mAB+AC-AC=mAB-AC,λNB=λ(AB-AN)=λ=λAB-AC,∴∴m=λ=.【答案】3.点M是△ABC所在平面内的一点,且满足AM=AB+AC,则△ABM与△ABC的面积之比为________.【解析】如图,分别在AB,AC上取点E,F,使AE=AB,AF=AC,在BC上取点G,使BG=BC,则EG∥AC,FG∥AE,∴AG=AE+AF=AM,∴M与G重合,∴==.【答案】4.如图2312,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB,AC于M,N两点,若AM=xAB,AN=yAC,试问:+是否为定值?图2312【解】设AB=a,AC=b,则AM=xa,AN=yb,AG=AD=(AB+AC)=(a+b),∴MG=AG-AM=(a+b)-xa=a+b,MN=AN-AM=yb-xa=-xa+yb.∵MG与MN共线,∴存在实数λ,使MG=λMN,∴a+b=λ(-xa+yb)=-λxa+λyb.∵a与b不共线,∴消去λ,得+=4,∴+为定值.3