高三数学：一道立体几何的思考(苏) 试题VIP免费

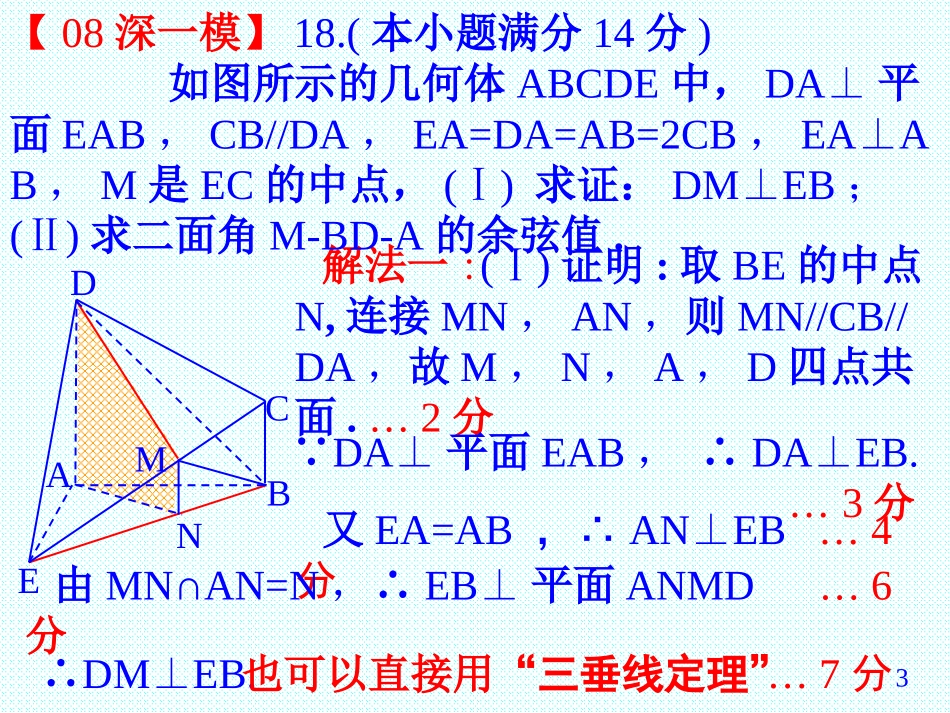
选自2006年广州市普通高中毕业班综合测试(一)概念清，路子正方法优，运算准2025年2月24日北大附中深圳南山分校高三数学组倪杰2奋斗拼博3ABCDEM解法一:()Ⅰ证明:取BE的中点N,连接MN，AN，则MN//CB//DA，故M，N，A，D四点共面.…2分N DA⊥平面EAB，∴DAEB.⊥…3分又EA=AB，∴ANEB⊥…4分由MN∩AN=N，∴EB⊥平面ANMD…6分∴DMEB.⊥…7分也可以直接用“三垂线定理”【08深一模】18.(本小题满分14分)如图所示的几何体ABCDE中，DA⊥平面EAB，CB//DA，EA=DA=AB=2CB，EAA⊥B，M是EC的中点，()Ⅰ求证：DMEB⊥；()Ⅱ求二面角M-BD-A的余弦值.4P设CB=a，AC与BD的交点为O，∠AOD=θCAB=α∠，QOABCDENM解:()Ⅱ取AC的中点P，连MP，则MP//EA，∴MP⊥平面ABCD，过P作PQBD⊥，连QM，则QMBD⊥，∴∠MQP是二面角M-BD-A的平面角9分则有COCB11==CO=ACAOAD23，，221115OP=()AC=a+(2a)=a2366，∴sinθ=sin(α+450)221232=(sinα+cosα)=(+)=2255252PQ=OPsinθ=a4又MP=0.5EA=a，在Rt△MPQ中，MPtanMQP==22PQ，即二面角M-BD-A的余弦值为…14分13…12分？5EDCBAMzyxa2解法二:分别以直线AE，AB，AD为x轴、y轴、z轴，建立如图所示的空间直角坐标系A-xyz，设CB=a，则A(0，0，0)，E(2a，0，0)，B(0，2a，0)，C(0，2a，a)，D(0，0，2a)，所以M(a，a，)……4分DMEB⊥，即DMEB⊥……7分()Ⅱ解:设平面MBD的法向量为n=(x，y，z)DB=(0，2a，－2a)由nDB⊥，nD⊥M得DM·EB=a(－2a)+a·2a+0=0(Ⅰ)证:DM=(a，a，－1.5a)，EB=(－2a，2a，0)，…5分6取z=2得平面MBD的一非零法向量为n=(1，2，2)，又平面BDA的法向量为n1=(1，0，0)，2222221+0+0==1+2+21+0+01.3cos即二面角M-BD-A的余弦值为…14分13…11分EDCBAMzyxnDB=2ay2az=03nDM=ax+ayaz=02����…10分y=z3x+yz=02此题用“坐标法”解简单易行！717.(本小题满分14分)如图，边长为2的线段AB夹在直二面角α-l-β的两个半平面内，Aα∈，Bβ∈，且AB与平面α、β所成的角都是300，AC⊥l垂足为C，BD⊥l，垂足为D.()Ⅰ直线AB与CD所成的角；()Ⅱ求二面角C-AB-D所成平面角的余弦值．lβαDCBA如何合理的选择正确的方法解“立几”题？通过解题的过程您将有会什么样的收获与启发？本节将以此题为例探索解决立体中有关角的问题的规律.由此我们联想[2006广州一模]一道立体几何题8②平移法:即根据定义，以“运动”的观点，用“平移转化”的方法使之成为相交直线所成的角.选择“特殊点”作异面直线的平行线，构作含异面直线所成(或其补角)的角的三角形，再求之.③补形法:把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体等，其目的在于易于发现两条异面直线的关系.①向量法:线线角可转化为两直线的方向向量所成的角.|ABCD|cosα=|AB||CD|��异面直线所成角的范围是:(0，900]求异面直线所成的角常用的方法有：一、异面直线所成的角根据异面直线所成角的定义，求异面直线所成角,就是要将其变换成相交直线所成有角.9二、直线和平面所成的角二、直线和平面所成的角直线与平面平行或在平面内直线和平面所成的角0º斜线和平面所成的角是：斜线及斜线在平面上的射影所成的角.关键是找准斜线段在平面内的射影；直线与平面垂直，直线和平面所成的角是90º；①直接法:通常是从斜线上找特殊点，作平面的垂线段构作含所求线面角的三角形求之.②公式法：求斜线与平面所成的角，还可以利用三面角的余弦公式：注:当余弦值为负值时其对应角为钝角，这不符合定义，故其补角为所求的角.αβγcosα=cosβcosγ10nAB③向量法|ABn|sinα=|AB||n|��线面角等于直线的方向向量与平面的法向量所成角的余角.线面角或等于直线的方向向量与平面的法向量所成角的补角的余角.αβγABCP在RtPAC△中，cosβ=ACAP在RtABC△中，cosγ=ABAC在RtPAB△中，cosα=ABAPACABABcosβcosγcosαAPACAPcosα=cosβcosγ112、二面角的平面角的作法：①定义法：点P在棱上根据定义作出来.αβlP②作垂面：点P在二面角内作与棱垂直的平面与两半平面的交线得到.AOBαβlP③应用三垂线：点A在一个半平面上应用三垂线定理或其逆定理作出来.BAOαβl三...