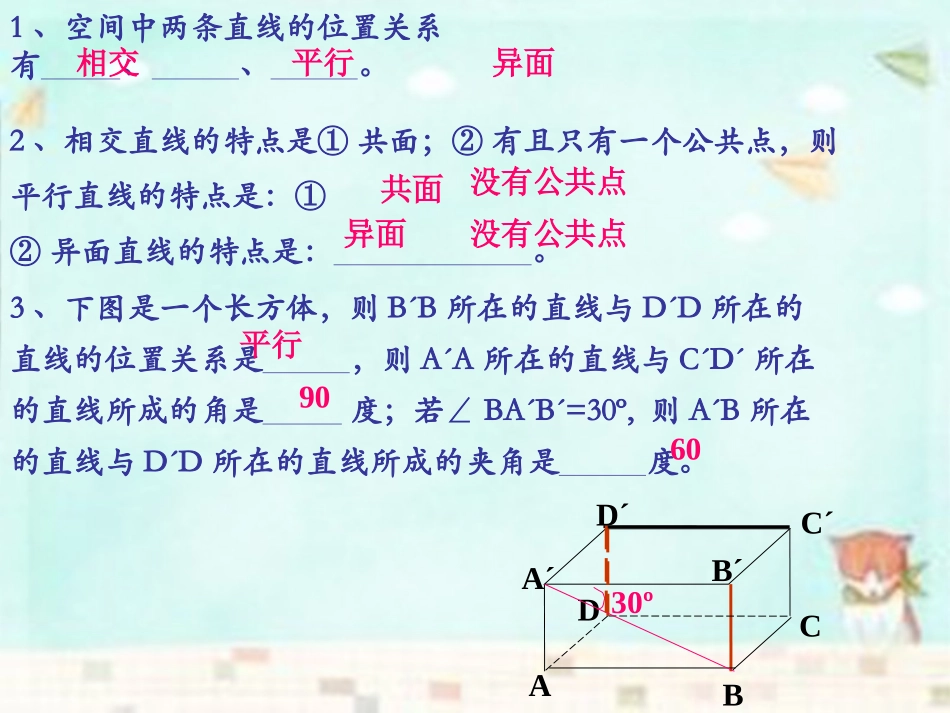
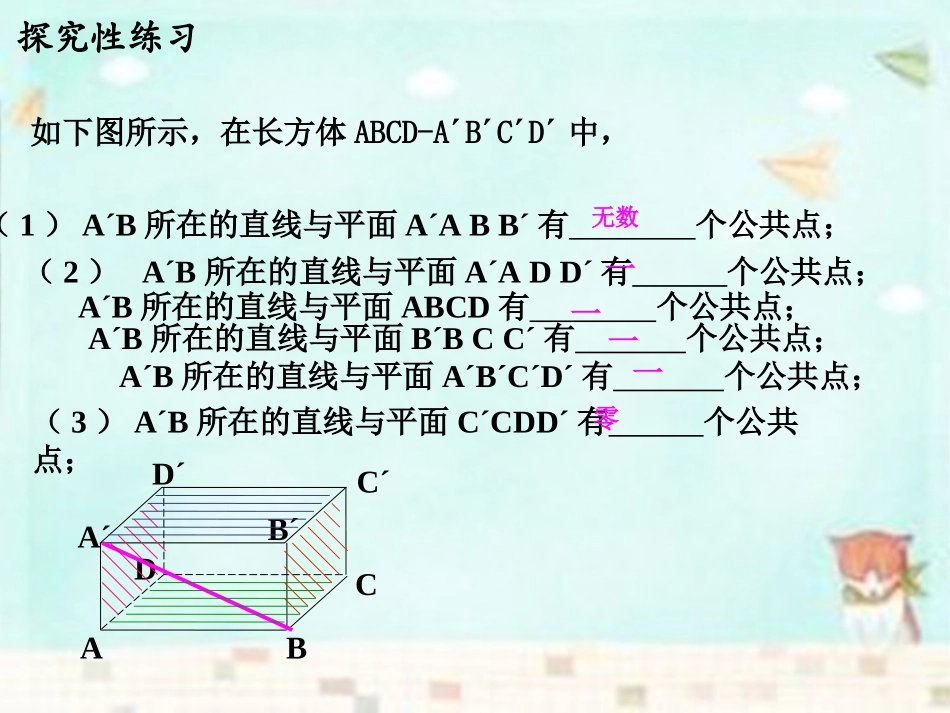
空间中直线与平面之间的位置关系3、下图是一个长方体,则B´B所在的直线与D´D所在的直线的位置关系是,则A´A所在的直线与C´D´所在的直线所成的角是度;若∠BA´B´=30º,则A´B所在的直线与D´D所在的直线所成的夹角是度。1、空间中两条直线的位置关系有、、。2、相交直线的特点是①共面;②有且只有一个公共点,则平行直线的特点是:①②异面直线的特点是:。ABCDA´B´C´D´30º相交平行异面共面没有公共点异面没有公共点平行9060探究性练习如下图所示,在长方体ABCD-A´B´C´D´中,(1)A´B所在的直线与平面A´ABB´有个公共点;(3)A´B所在的直线与平面C´CDD´有个公共点;CDA´B´C´D´AB(2)A´B所在的直线与平面A´ADD´有个公共点;A´B所在的直线与平面B´BCC´有个公共点;A´B所在的直线与平面A´B´C´D´有个公共点;A´B所在的直线与平面ABCD有个公共点;无数一一一一零③直线与平面平行——没有公共点;1、交流归纳:直线与平面的位置关系有且只有三种:①直线在平面内——有无数个公共点(交点);②直线与平面相交——有且只有一个公共点;α2、如何用图形语言表示直线与平面的三种位置关系?aa①α③二、新课aα②错误画法:αaα②①aaα③3、如何用符号语言表示直线与平面的位置关系。①直线a在平面α内,记作aα;②直线a与平面α相交于A点,记作a∩α=A;③直线a与平面α平行,记作a∥α;例1.空间四边形相邻两边中点的连线,平行于经过另外两边的平面.已知:空间四边形ABCD中,E、F分别是AB、AD的中点.求证:EF∥平面BCD.证明:连结BD.性,这三个条件是证明直线和平面平行的条件,缺一不可.例2判断下列四个命题的对错.(1)若直线l上有无数个点不在平面α内,则l∥α.(2)若直线l与平面α平行,则l与平面α内的任意一条直线都平行.(3)若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.(4)若两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.(×)(×)(×)()随堂练习1、若直线a不平行于平面α,且aα,则下列结论成立的是():(A)α内的所有直线与a异面;(B)α内不存在与a平行的直线;(C)α内存在唯一的直线与a平行;(D)α内的直线与a都相交;2、判断题:(1)a∥α,bα,则a∥b;()(2)aα,则a∥α或a和α相交;()(3)a∩α=A,aα;()(4)若aα,bα,则a、b无公共点。()B×√√×aαbαbabaαc四、小结:1、空间中直线与平面的三种位置关系:直线在平面内——有无数个公共点(交点);直线在平面外相交——有且只有一个公共点;平行——没有公共点;2、用图形语言表示空间中直线与平面的三种位置关系:3、用符号语言表示空间中直线与平面的三种关系:①aα②a∩α=A③a∥αααa①②aα③a1.已知直线a在平面α外,则()(A)a∥α(B)直线a与平面α至少有一个公共点(C)aα=A(D)直线a与平面α至多有一个公共点。奎屯王新敞新疆随堂检测D2.选择题(1)以下命题(其中a,b表示直线,表示平面)①若a∥b,b,则a∥②若a∥,b∥,则a∥b③若a∥b,b∥,则a∥④若a∥,b,则a∥b其中正确命题的个数是()(A)0个(B)1个(C)2个(D)3个A3.已知a∥,b∥,则直线a,b的位置关系①平行;②垂直不相交;③垂直相交;④相交;⑤不垂直且不相交.其中可能成立的有()(A)2个(B)3个(C)4个(D)5个4.如果平面外有两点A、B,它们到平面的距离都是a,则直线AB和平面的位置关系一定是()(A)平行(B)相交(C)平行或相交(D)ABDC5.已知m,n为异面直线,m∥平面,n∥平面,∩=l,则l()(A)与m,n都相交(B)与m,n中至少一条相交(C)与m,n都不相交(D)与m,n中一条相交C探究(一)平面与平面之间的位置关系思考1:拿出两本书,看作两个平面,上下、左右移动和翻转,它们之间的位置关系有几种变化?思考2:如图,围成长方体ABCD-A′B′C′D′的六个面,两两之间的位置关系有几种?C′A′B′D′ABCD思考3:由上面的观察和分析可知,两个平面的位置关系只有两种,即两个平面平行,两个平面相交.这两种位置关系的基本特征是什么...