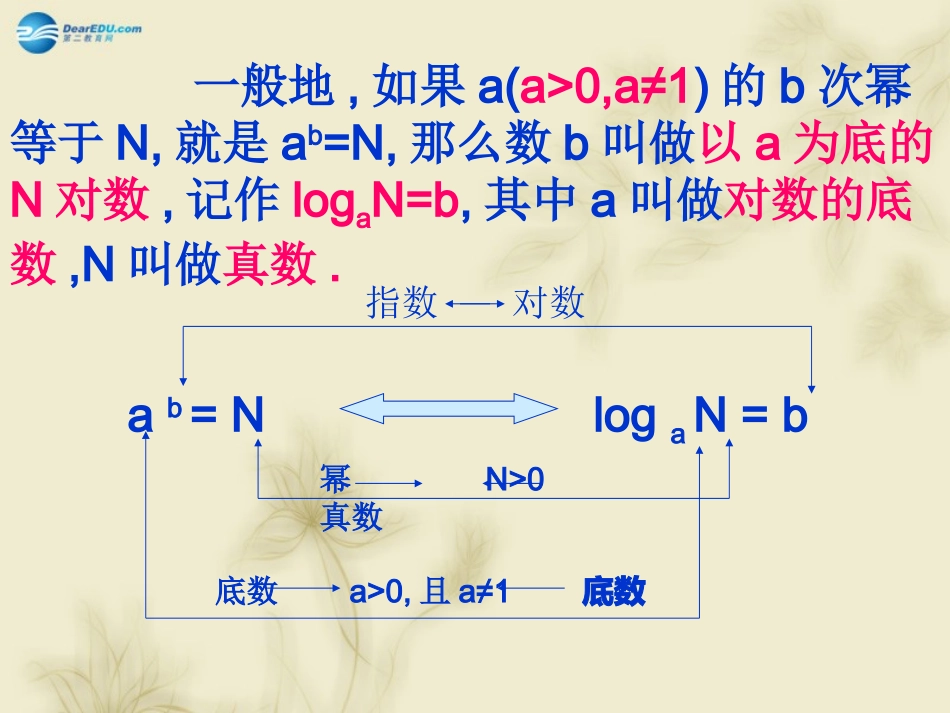
对数已知指数b,幂N,求底数a开方运算,根式,其中a:方根,b:根指数,N:被开方数其中a>0且a≠1,b€R,N>0已知底数a,指数b,求幂N乘方运算N=ab,指数式,其中a:底数,b:指数,N:幂已知底数a,幂N,求指数b对数运算b=logaN,对数式,其中a:底数,b:对数,N:真数实数指数幂ab=NbNa一般地,如果a(a>0,a≠1)的b次幂等于N,就是ab=N,那么数b叫做以a为底的N对数,记作logaN=b,其中a叫做对数的底数,N叫做真数.ab=NlogaN=b幂N>0真数底数a>0,且a≠1底数指数对数因此,要使对数logaN有意义必须有底数a>0并且a≠1和真数N>0几个重要结论(其中a>0且a≠0,N>0)1零和负数没有对数2logaa=13loga1=04alogaN=NWhy?特殊常用的两种对数(1)常用对数以10为底的对数叫做常用对数,即对数logaN(a>0且a≠1)(N>0)在底数a=10时,叫做常用对数,N的常用对数log10N简记作lgN例如log105=lg5(2)自然对数以无理数e=2.71828······为底的对数叫做自然对数,即对数logaN(a>0且a≠1)(N>0)在底数a=e时,叫做自然对数,N的自然对数logeN简记作lnN例如loge5=ln5lg10=1,lg1=0lne=1,ln1=0例1.将下列指数式写成对数式mexxma)6(710)5(73.5)31)(4(273)3(6412)2(6255)1(64例2.将下列对数式写成指数式303.210ln)4(201.0lg)3(7128log)2(416log)1(221对数的运算性质NMMNaaaloglog)(log)(1NMaaNMalogloglog)(2MnManaloglog)3(RnNMaa,0,0,1,0且其中,abbccalogloglog)4(bbamnnamloglog)5(1loglog)6(abba例3用logax,logay,logaz表示下列各式32log)2(log)1(zyxzxyaa例4求下列各式的值5572100lg)2()24(log)1(