高中数学 变化率问题、导数的概念优质课件(选修1 1) 课件VIP免费

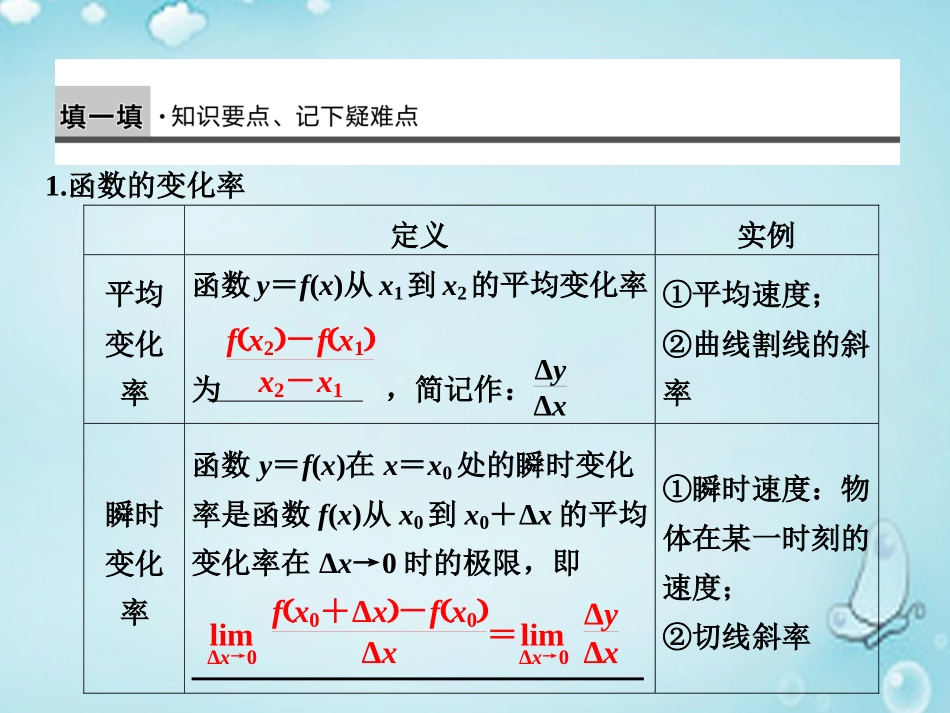
1.函数的变化率定义实例平均变化率函数y＝f(x)从x1到x2的平均变化率为，简记作：ΔyΔx①平均速度；②曲线割线的斜率瞬时变化率函数y＝f(x)在x＝x0处的瞬时变化率是函数f(x)从x0到x0＋Δx的平均变化率在Δx→0时的极限，即①瞬时速度：物体在某一时刻的速度；②切线斜率limΔx→0fx0＋Δx－fx0Δx＝limΔx→0ΔyΔxfx2－fx1x2－x12.函数f(x)在x＝x0处的导数函数y＝f(x)在x＝x0处的称为函数y＝f(x)在x＝x0处的导数，记作，即f′(x0)＝.f′(x0)或y′|x＝x0limΔx→0ΔyΔx＝limΔx→0fx0＋Δx－fx0Δx瞬时变化率引言某市2012年5月30日最高气温是33.4℃，而此前的两天5月29日和5月28日最高气温分别是24.4℃和18.6℃，短短两天时间，气温“陡增”14.8℃，闷热中的人们无不感叹：“天气热得太快了！”但是，如果我们将该市2012年4月28日最高气温3.5℃和5月28日最高气温18.6℃进行比较，可以发现二者温差为15.1℃，甚至超过了14.8℃，而人们却不会发出上述感慨，这是什么原因呢？显然原因是前者变化得“太快”，而后者变化得“缓慢”，那么在数学中怎样来刻画变量变化得快与慢呢？探究点一平均变化率的概念问题1气球膨胀率我们都吹过气球，回忆一下吹气球的过程，可以发现，随着气球内空气容量的增加，气球的半径增加得越来越慢.从数学的角度，如何描述这种现象呢？答案气球的半径r(单位：dm)与体积V(单位：L)之间的函数关系是r(V)＝33V4π，(1)当V从0增加到1L时，气球半径增加了r(1)－r(0)≈0.62(dm)，气球的平均膨胀率为r1－r01－0≈0.62(dm/L).(2)当V从1L增加到2L时，气球半径增加了r(2)－r(1)≈0.16(dm)，气球的平均膨胀率为r2－r12－1≈0.16(dm/L).可以看出，随着气球体积逐渐增大，它的平均膨胀率逐渐变小了.结论当空气容量从V1增加到V2时，气球的平均膨胀率是rV2－rV1V2－V1.问题2高台跳水在高台跳水运动中，运动员相对于水面的高度h(单位：m)与起跳后的时间t(单位：s)存在函数关系h(t)＝－4.9t2＋6.5t＋10.计算运动员在下列时间段内的平均速度v，并思考平均速度有什么作用？①0≤t≤0.5，②1≤t≤2.答案①在0≤t≤0.5这段时间里，v＝h0.5－h00.5－0＝4.05(m/s)；②在1≤t≤2这段时间里，v＝h2－h12－1＝－8.2(m/s).由以上计算体会到平均速度可以描述运动员在某段时间内运动的快慢.问题3什么是平均变化率，平均变化率有何作用？答案如果问题中的函数关系用y＝f(x)表示，那么问题中的变化率可用式子fx2－fx1x2－x1表示，我们把这个式子称为函数y＝f(x)从x1到x2的平均变化率，平均变化率可以描述一个函数在某个范围内变化的快慢.问题4平均变化率也可以用式子ΔyΔx表示，其中Δy、Δx的意义是什么？ΔyΔx有什么几何意义？答案Δx表示x2－x1是相对于x1的一个“增量”；Δy表示f(x2)－f(x1).Δx、Δy的值可正可负，Δy也可以为零，但Δx不能为零.观察图象可看出，ΔyΔx表示曲线y＝f(x)上两点(x1，f(x1))、(x2，f(x2))连线的斜率.例1已知函数f(x)＝2x2＋3x－5.(1)求当x1＝4，且Δx＝1时，函数增量Δy和平均变化率ΔyΔx；(2)求当x1＝4，且Δx＝0.1时，函数增量Δy和平均变化率ΔyΔx；(3)若设x2＝x1＋Δx.分析(1)(2)题中的平均变化率的几何意义.解f(x)＝2x2＋3x－5，∴Δy＝f(x1＋Δx)－f(x1)＝2(x1＋Δx)2＋3(x1＋Δx)－5－(2x21＋3x1－5)＝2[(Δx)2＋2x1Δx]＋3Δx＝2(Δx)2＋(4x1＋3)Δx.(1)当x1＝4，Δx＝1时，Δy＝2＋(4×4＋3)×1＝21，ΔyΔx＝211＝21.(2)当x1＝4，Δx＝0.1时，Δy＝2×0.12＋(4×4＋3)×0.1＝0.02＋1.9＝1.92，ΔyΔx＝1.920.1＝19.2.(3)在(1)题中ΔyΔx＝fx2－fx1x2－x1＝f5－f45－4，它表示抛物线上P0(4,39)与点P1(5,60)连线的斜率.在(2)题中，ΔyΔx＝fx2－fx1x2－x1＝f4.1－f44.1－4，它表示抛物线上点P0(4,39)与点P2(4.1,40.92)连线的斜率.小结求平均变化率的主要步骤：(1)先计算函数值的改变量Δy＝f(x2)－f(x1).(2)再计算自变量的改变量Δx＝x2－x1.(3)得平均变化率ΔyΔx＝fx2－fx1x2－x1.跟踪训练1(1)计算函数f(x)＝x2从x＝1到x...